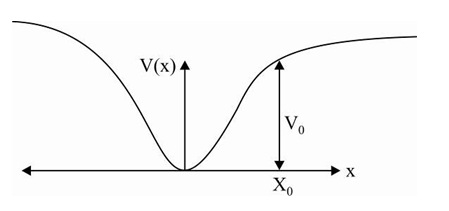
When a particle of mass m moves on the x-axis in a potential of the form v(x)=kx2 it performs simple harmonic motion. The corresponding time period is proportional to m, k as can be seen easily using dimensional analysis. However, the motion of particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the x-axis. Its potential energy is v(x)=ax4(a>0)for |x| near the origin and becomes a constant equal to v0 for|x|≥X0.
Q If the total energy of the particle is E, it will perform periodic motion only if :
E<0
E>0
V0>E>0
E>V0
The correct Answer is:C
When 0<E<V0 there will be acting a restoring force to perform oscillation because in this case paticle will be in the region |x|≤x0.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 3, PART - II
17 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - IV
8 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
Similar Questions
When a particle is mass m moves on the x− axis in a potential of the from V(x)=kx2, it performs simple harmonic motion. The corresponding thime periond is proportional to √mk, as can be seen easily asing dimensional analysis. However, the motion of a pariticle can be periodic even when its potential enem increases on both sides x=0 in a way different from kx2 and its total energy is such that the particel does not escape to infinity. consider a particle of mass m moving onthe x−axis . Its potential energy is V(x)=ω(α>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0 (see figure)
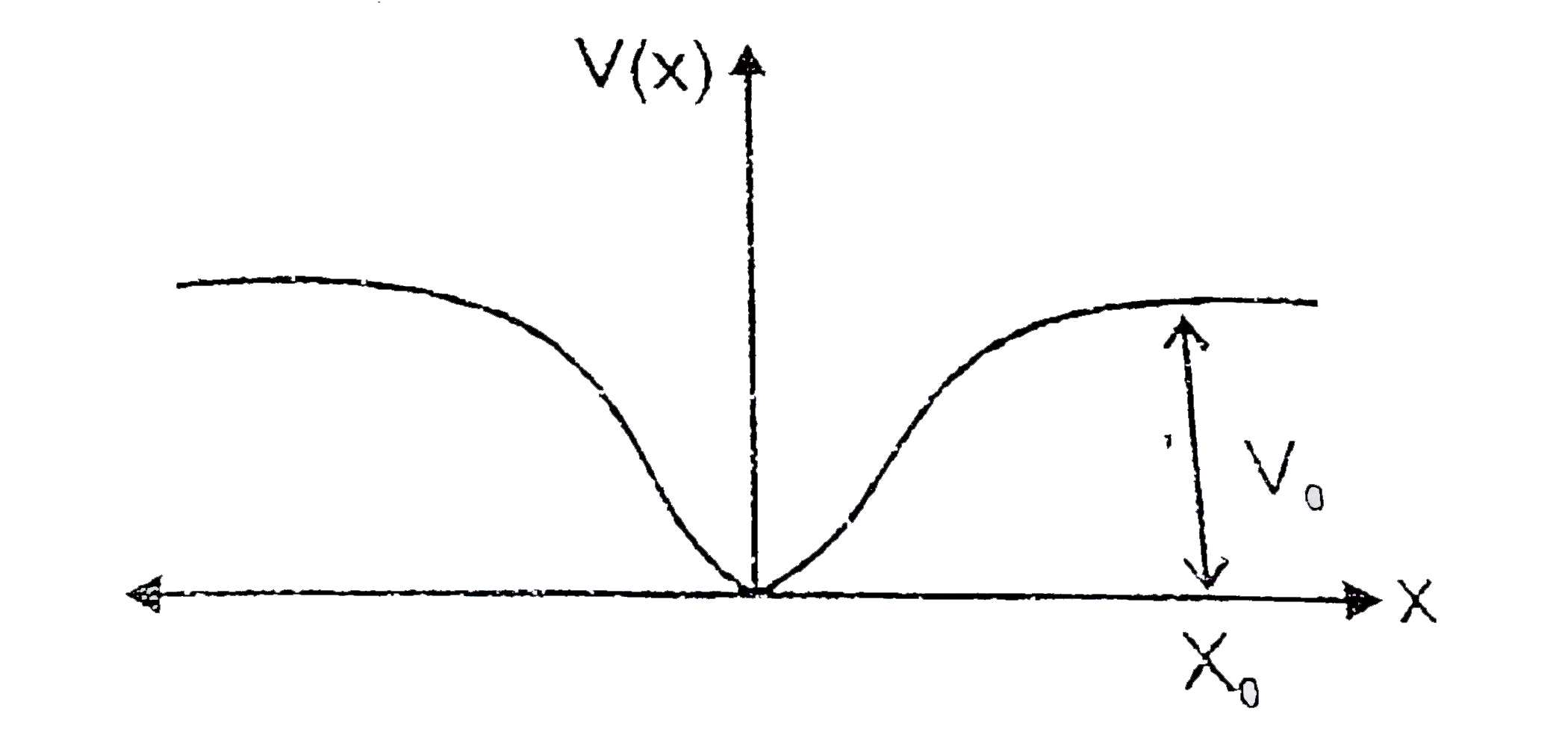
If the total energy of the particle is E, it will perform is periodic motion why if :
View SolutionWhen a particle is mass m moves on the x− axis in a potential of the from V(x)=kx2, it performs simple harmonic motion. The corresponding thime periond is proportional to √mk, as can be seen easily asing dimensional analysis. However, the motion of a pariticle can be periodic even when its potential enem increases on both sides x=0 in a way different from kx2 and its total energy is such that the particel does not escape to infinity. consider a particle of mass m moving onthe x−axis . Its potential energy is V(x)=ω(α>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0 (see figure)

If the total energy of the particle is E, it will perform is periodic motion why if :
View Solution
Knowledge Check
A particle is executing simple harmonic motion. Its total energy is proportional to its
Adisplacement from equilibrium positionBfrequency of oscillationCsquare of amplitude of motionDvelocity at equilibrium position
When a particle is mass m moves on the x− axis in a potential of the from V(x)=kx2, it performs simple harmonic motion. The corresponding thime periond is proportional to √mk, as can be seen easily asing dimensional analysis. However, the motion of a pariticle can be periodic even when its potential enem increases on both sides x=0 in a way different from kx2 and its total energy is such that the particel does not escape to infinity. consider a particle of mass m moving onthe x−axis . Its potential energy is V(x)=ω(α>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0 (see figure)

If the total energy of the particle is E, it will perform is periodic motion why if :
View SolutionWhen a particle is mass m moves on the x− axis in a potential of the from V(x)=kx2, it performs simple harmonic motion. The corresponding thime periond is proportional to √mk, as can be seen easily asing dimensional analysis. However, the motion of a pariticle can be periodic even when its potential enem increases on both sides x=0 in a way different from kx2 and its total energy is such that the particel does not escape to infinity. consider a particle of mass m moving onthe x−axis . Its potential energy is V(x)=ω(α>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0 (see figure)

If the total energy of the particle is E, it will perform is periodic motion why if :
View SolutionWhen a particle of mass m moves on the x-axis in a potential of the form V(x)=kx2 it performs simple harmonic motion. The correspondubing time period is proprtional to √mh, as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x=0 in a way different from kx2 and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x)=ax4(a>0) for |x| neat the origin and becomes a constant equal to V0 for |x|impliesX_(0)(seefigure).<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/JMA_CHMO_C10_033_Q01.pngwh=80%mx-autosty≤=background:white;>.<br>Theae≤rationofthisparti≤for|x|gtX_(0)is<br>(a)∝rtional→V_(0)
(b) proportional to.
View SolutionThe distance moved by a particle in simple harmonic motion in one time period is
View SolutionThe total energy of a particle having a displacement x, executing simple harmonic motion is
View SolutionA particle moves on the X-axis according to the equation x=x0sin2ωt. The motion simple harmonic
View SolutionA particle moves on the X-axis according to the equation x=5sin2ωt. The motion simple harmonic
View Solution
