A particle of mass m is attached to one end of a mass-less spring of force constant k, lying on a frictionless horizontal plane. The other end of the spring is fixed. The particle starts moving horizontally from its equilibrium position at time with an initial velocity . when the speed of the particle is , it collides elastically with a rigid wall. After this collision
the speed to the particle when its returns to its equilibrium is .
the time is at which paricle passes through the equilirbium position for the first time is .
the time at which the maximum compression of the spring occurs is .
the time at which the particles passes throuhout the equilirbium position for the second time is .
The correct Answer is:A, D
To solve the problem step-by-step, we will analyze the motion of the particle attached to the spring and its interaction with the wall.
Step 1: Understand the Initial Conditions
- The particle of mass m is attached to a spring with spring constant k.
- It starts from the equilibrium position with an initial velocity u0 at t=0.
Hint: Remember that the equilibrium position is where the spring is neither compressed nor stretched.
Step 2: Determine the Time of Collision
- The particle moves in simple harmonic motion (SHM). The velocity of a particle in SHM can be expressed as:
v(t)=u0cos(ωt)
where ω=√km.
- We need to find the time t1 when the speed of the particle is 0.5u0:
0.5u0=u0cos(ωt1)
Simplifying gives:
cos(ωt1)=0.5
This implies:
ωt1=π3
Therefore:
t1=π3ω
Hint: Use the properties of cosine to find angles corresponding to given values.
Step 3: Determine the Time of Return to Equilibrium
- The particle returns to the equilibrium position after a complete cycle of SHM. The time taken to return to equilibrium after the first collision is t2=2t1:
t2=2⋅π3ω=2π3ω
Hint: The motion of the particle is periodic; each complete cycle takes a certain time.
Step 4: Calculate the Time of the Second Pass Through Equilibrium
- The time t3 when the particle passes through the equilibrium position for the second time is:
t3=t2+t1=2π3ω+π3ω=5π3ω
Hint: Keep track of the time intervals for each segment of the motion.
Step 5: Analyze the Collision with the Wall
- The collision with the wall is elastic, meaning the speed of the particle will reverse direction but maintain its magnitude. Thus, after the collision, the speed will still be 0.5u0 but in the opposite direction.
Hint: In elastic collisions, both momentum and kinetic energy are conserved.
Step 6: Determine the Speed When Returning to Equilibrium
- After the collision, the particle will continue its motion and eventually return to the equilibrium position. The speed at this point will be equal to its initial speed u0 because the energy in the system remains conserved.
Hint: The total mechanical energy in SHM remains constant, allowing you to deduce speeds at various points.
Final Conclusion
- The speed of the particle when it returns to the equilibrium position after the collision will be u0.
Final Answer: The speed of the particle when it returns to equilibrium is u0.
- The particle of mass m is attached to a spring with spring constant k.
- It starts from the equilibrium position with an initial velocity u0 at t=0.
- The particle moves in simple harmonic motion (SHM). The velocity of a particle in SHM can be expressed as:
v(t)=u0cos(ωt)
where ω=√km.
- We need to find the time t1 when the speed of the particle is 0.5u0:
0.5u0=u0cos(ωt1)
Simplifying gives:
cos(ωt1)=0.5
This implies:
ωt1=π3
Therefore:
t1=π3ω
- The particle returns to the equilibrium position after a complete cycle of SHM. The time taken to return to equilibrium after the first collision is t2=2t1:
t2=2⋅π3ω=2π3ω
- The time t3 when the particle passes through the equilibrium position for the second time is:
t3=t2+t1=2π3ω+π3ω=5π3ω
- The collision with the wall is elastic, meaning the speed of the particle will reverse direction but maintain its magnitude. Thus, after the collision, the speed will still be 0.5u0 but in the opposite direction.
- After the collision, the particle will continue its motion and eventually return to the equilibrium position. The speed at this point will be equal to its initial speed u0 because the energy in the system remains conserved.
- The speed of the particle when it returns to the equilibrium position after the collision will be u0.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 3, PART - II
Explore 17 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - IV
Explore 8 Videos
- SEMICONDUCTORSBook:RESONANCE ENGLISHChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PHYSICS
Explore 784 Videos
Similar Questions
A particle of mass 3 kg , attached to a spring with force constant 48Nm−1execute simple harmonic motion on a frictionless horizontal surface. The time period of oscillation of the particle, is seconds , is
View SolutionA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View Solution
Knowledge Check
A 10 kg mass is connected at one end of a massless spring with force constant k = 1000 N/m, keeping other end fixed in a horizontal plane as shown in the fig. 15.6
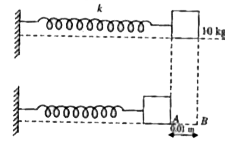 If the sytem is displaced by 0.01 m from its equilibrium position A to a point B, then the acceleration of the system is A10ms−2B1ms−2C−1ms−2D−10ms−2
If the sytem is displaced by 0.01 m from its equilibrium position A to a point B, then the acceleration of the system is A10ms−2B1ms−2C−1ms−2D−10ms−2
A particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl

The maximum angle made by the string with downward vertical is
View SolutionA mass of 0.2 kg is attached to the lower end of a massless spring of force constant 200Nm the other end of which is fixed to a rigid support. Study the following statements.
View SolutionA block of mass m is kept on a rough horizontal surface and is attached with a massless spring of force constant k. The minimum constant force applied on the other end of the spring of lift the block is
View SolutionA particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is

View SolutionA mass of 0.2 hg is attached to the lower end of a massles spring of force constant 200Nm the opper end of which is fixed to a rigid support. Study the following statements.
View SolutionA block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View Solution

