A particle of mass 'm' moves on a horizont smooth line AB of length 'a' such that when particle is at any general point P on the line two force act on it. A force mg(AP)a towards A and another force 2mg(BP)a towards B. particle released from rest from mid point of AB.
Find the minimum distance of the particle from B during the motion.
√2ga3
√2ga6
√2ga5
√ga3
The correct Answer is:B
(i) force on particle at point P
f=2mg(a−x)a−mg(x)a
F=mga(2a−3x)
m F=−3mga(x−2a/3)

(ii) So this is equation of S.H.M.(F=mω2x) so particle
Perform S.H.M. with mean position x−2a/3=0
So ω2=3ga⇒ω=√3g/a
So Time period T=2π√a/3g
and amplitude =2a/3−a/2=a/6
(iii) minimum distance from B
=a−(2a/3+a/6)=a/6
(iv) at point P velocity of partivle =0
and force =2mgxa
(at point q)
acc. =2gxa⇒v∫ovdv=a/6∫o2gxdxa⇒V=√2ga6

Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 3, PART - I
Explore 20 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 3, PART - II
Explore 17 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - III
Explore 12 Videos
- SEMICONDUCTORSBook:RESONANCE ENGLISHChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PHYSICS
Explore 784 Videos
Similar Questions
A simple pendulum has time period T1. The point of suspension is now moved upward according to the relation y=Kt2. (K=1ms−2) where y is the vertical displacement. The time period now becomes T2
The ratio of T21T22(Take g=10ms−2)
View SolutionIf a simple harmonic motion is represented by d2xdt2+αx=0, its time period is
View SolutionA particle moves on the X-axis according to the equation x=x0sin2ωt. The motion simple harmonic
View SolutionWhen p−n junction diode is forward biased, then
View SolutionTwo particles are intially at a separation of d to each other. They move with constant velocirties with 5m/s and 3m/s respectively in horizontal plane. Their velocities makes an angle 60∘ with each other. If after 2 seconds, they collide. Then value of d is:
View SolutionA particle of mass 4 kg moves between two points A and B on a smooth horizontal surface under the aciton of two forces such that when it is at a point P , the forces are 2vec(P)AN and 2vec(P)B N . If the particle is released from rest at A, find the time it takes to travel a quarter of the way A to B .
View SolutionTwo strange particles A and B in space, exert no force on each other when they are at a separation greater than x_(0) = 1.0 m. When they are at a distance less than x_(0) , they repel one another along the line joining them. The repulsion force is constant and does not depend on the distance between the particles. This repulsive force produces an acceleration of 6 ms^(–2) in A and 2 ms^(–2) in B when the particles are at separation less than x_(0) . In one experiment particle B is projected towards A with a velocity of 2 ms^(–1) from a large distance so as to hit A head on. The particle A is originally at rest and the system of two particles do not experience any external force. (a) Find the ratio of mass of A to that of B. (b) Find the minimum distance between the particles during subsequent motion. (c) Find the final velocity of the two particles.
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
What it is the time period of periodic motion of particle.
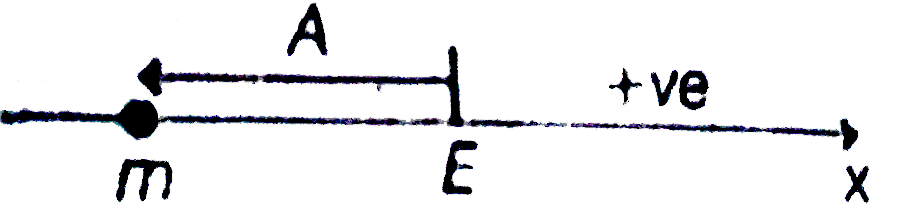
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
Velocity-time graph of the particle is
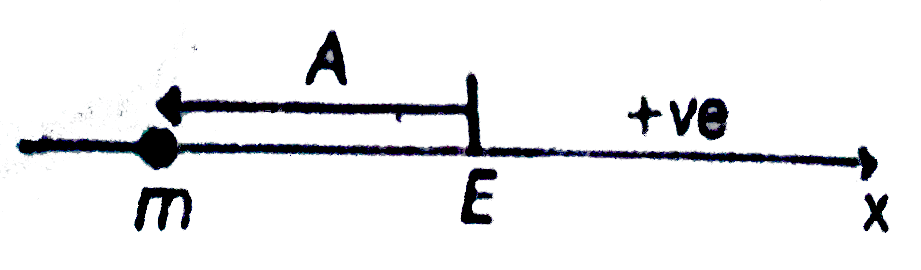
View SolutionA particle of mass 'm' moves on a horizont smooth line AB of length 'a' such that when particle is at any general point P on the line two force act on it. A force (mg(AP))/(a) towards A and another force (2mg(BP))/(a) towards B . Find the minimum distance of the particle from B during the motion.
View SolutionA particle of mass 'm' moves on a horizont smooth line AB of length 'a' such that when particle is at any general point P on the line two force act on it. A force (mg(AP))/(a) towards A and another force (2mg(BP))/(a) towards B . If the force acting towards A stops acting when the particle is nearest to B then find the velocity with which it crosses point B.
View SolutionA particle of mass 'm' moves on a horizont smooth line AB of length 'a' such that when particle is at any general point P on the line two force act on it. A force (mg(AP))/(a) towards A and another force 2(mg(BP))/(a) towards B . Find its time period when released from rest from mid-point of line AB .
View Solutionकोई कण एक-दूसरे से 10cm कम दूर पर स्थिर दो बिंदुओं A तथा B के बीच रैखिक सरल आवर्त गति कर रहा है। A से B की ओर दिशा को धनात्मक दिशा मानकर वेग, त्वरण तथा कण पर लगे बल के चिन्ह ज्ञात कीजिए जबकि यह कण
(a) A सिरे पर है,
(b) B सिरे पर है,
(c) Aकी ओर जाते हुए AB के मध्य-बिंदु पर है,
(d) A की ओर जाते हुए B से 2cm दूर है,
(e) B की ओर जाते हुए A से 3cm दूर है, तथा
A की ओर जाते हुए B से 4cm दूर है,
View Solutionएक कण सरंक्षी बल क्षेत्र में बिंदु A से B तक गति करता है। यदि A व B कण की स्थितिज ऊर्जाएं क्रमश : UAवUB हैं तथा सरंक्षी बल द्वारा कण को A से B तक ले जाने में किया गया कार्य WC है तो
View SolutionM1 तथाM2 द्रव्यमान के दो कण 'd' दूरी पर विरामावस्था में स्थित है। दोनों कणों को मिलाने वाली रेखा पर एक तीसरा कण इस प्रकार स्थित है कि इस पर कोई गुरूत्वाकर्षण बल नहीं लगता है। इस कण की M1 से दूरी ज्ञात कीजिये।
View SolutionA particle is in linear S.H.M. between two points A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it at the mid point of AB going towards A.
View Solution