The string, spring and the pulley shown in figure are light. Find the time period of the mass m.

Force Method
Let in equilibrium position of the block, extension in spring is x0.
∴Kx0−1
Now if we displace the block by x in the downward direction, net force on the block towards mean position is
F=k(x+x0)−mg,=kx using (1)
Hence the net force is acting towards mean position and is also propotional to x. So, the particle will perform S.H.M. and its time period would be
T=2π√mk
(b) Energy Method
Let gravitational potential energy is to be zero at the level of the block when spring is in its natural length.
Now at a distance x below that level, let speed of the block be v.
Since total mechcanical energy is conserved in S.H.M.
∴−mgx+12kx2+12mv2=constant
Differentiating w.r.t. time, we get
−mgv+kxv+mva=0
where a is accleration.
∴F=ma=−kx+mg or F=−k(x−mgk)
This shows that for the motion, force constant is k and equilibrium position is x=mgk.
So, the particle will perform S.H.M and its timne period would be T=2π√mk
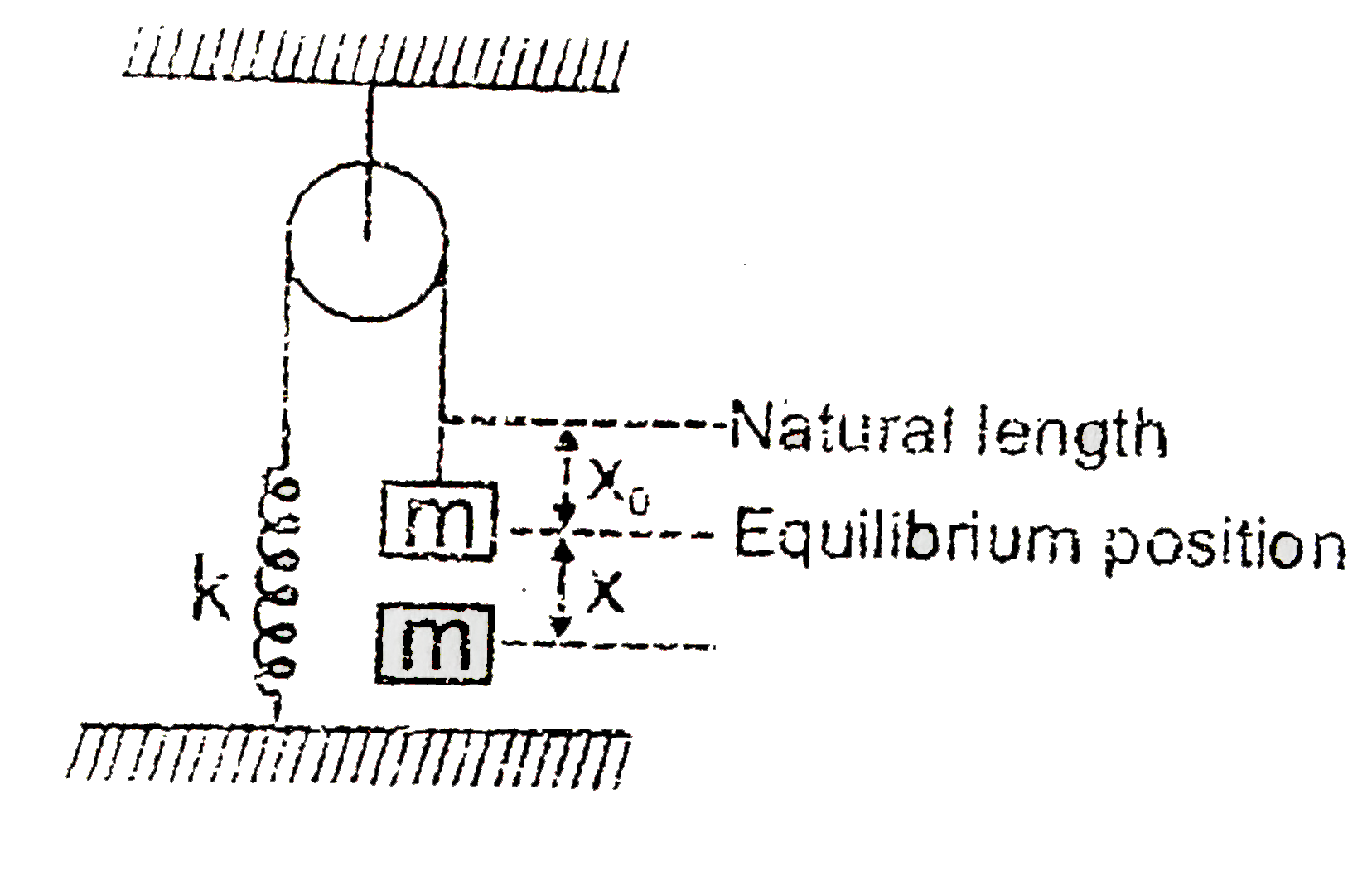
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Solved Miscellaneous Problems
Explore 9 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Board Level Exercise
Explore 24 Videos
- SEMICONDUCTORSBook:RESONANCE ENGLISHChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PHYSICS
Explore 784 Videos
Similar Questions
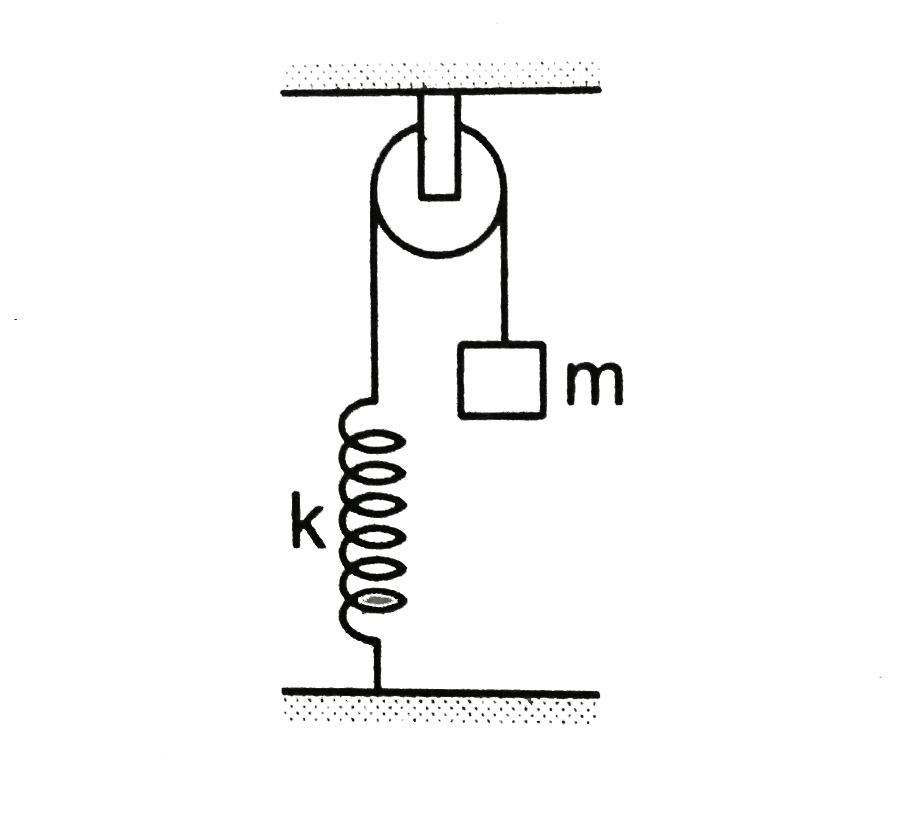
The string the spring and the puley shown in figure are light. Find the time period of the mass m.
View SolutionConsider the situation shown in the figure. The surface is smooth and the string and the pulley are light. Find the acceleration of each block and tension in the string.

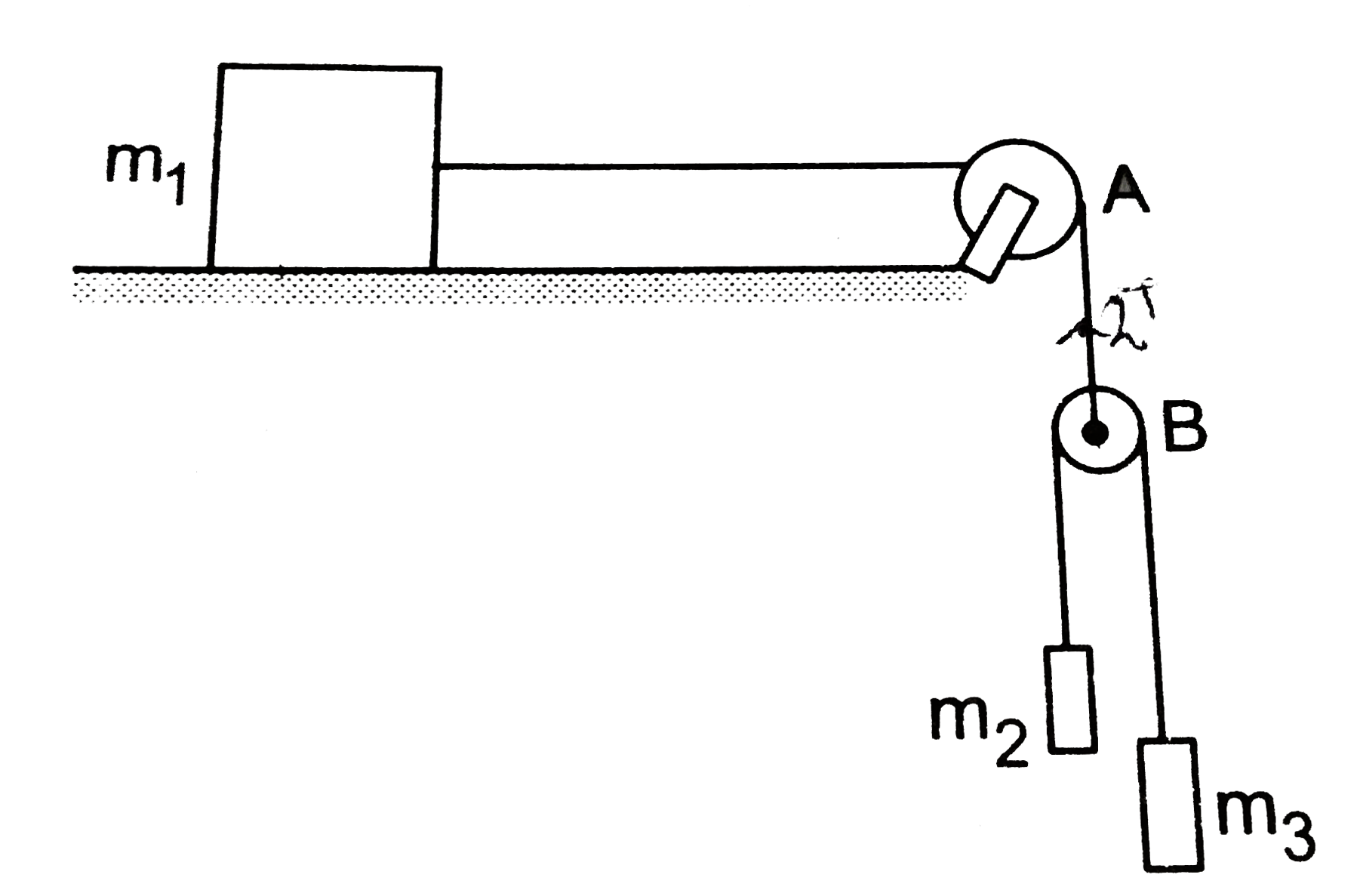
View SolutionThree blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
View SolutionSpring mass system is shown in figure. find the time period of vertical oscillations. The system is in vertical plane.

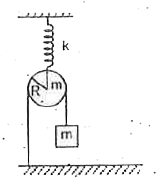
View SolutionConsider the situation shown in the figure. A mass is hanging from a inextensible string which is passing over a pulley. The pulley itself is attached to a massless spring of stiffness k as shown in the figure. Find the time period of vertical oscillations of mass m if pulley is slightly displaced from its mean position. Assume that string does not slip over pulley.
View SolutionThree blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1

View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is

View SolutionIn the arrangement shown, all the surface are smooth, strings and pulleys are light. Find the tension in the string.
View SolutionA uniform cubical block of mass M is attached to a pulley. One end of a string, passing over the pulley is fixed to a light pole while is fixed on the bigger block and its another end is attached to a block of mass m as shown in figure. The maximum value of the mass m so that the block does not topple is : (string and pulley are ideal)

View SolutionA block of mass m is attached to a cart of mass 4m through spring of spring constant k as shown in the figure. Friction is absent everywhere. The time period of oscillations of the system, when spring is compressed and then released, is

View Solution