A series LCR circuit is connected to an ac source having voltage v=vmsinωt. Derive the expression for the instantaneous current I and its phase relationship to the applied voltage.
(i) Maximum and (ii) minimum.
v=vmsinωt
Let the current in the circuit be lead the applied voltage by an angle ϕ.
i=imsin(ωt+ϕ)
The Kirchhoff's voltage law gives L=didt+Ri+qC=v
It is given that v=vmsinωt(applied voltage)
Ld2qdt2+Ridqdt+qC=vmsinωt..(1)
On solving the equation , we obtain q=qmsin(ωt+θ)
dqdt=qmωcos(ωt+θ)
d2qdt2=−qmω2sin(ωt+θ)
On substituting these values in equation (1), we obtain
qmω[Rcos(ωt+θ)+(XC−XL)sin(ωt+θ)]=vmsinωt XC=1ωC,X1=ωL
Z=√R2+(XC−XL)2
qmωZ[RZcos(ωt+R)+(XC−XL)Zsin(ωt+θ)]=vmsinωt....(2)
Let cosϕ=RZ and (XC−XL)Z=sinϕ
This gives tanϕ=(XC−XL)R
On substituting this in equation (2), we obtain
qmωZcos(ωt+θ−ϕ)=vmsinωt
On comparing the two sides , we obtain
vm=qmωZ=imZ
im=qmω
and θ=−π2+ϕ
i=dqdt=qmωcos(ωt+θ)=imcos(ωt+θ)
or i=imsin(ωt+θ)
Where im=vmZ=vm√R2+(XC−X2L)
And ϕ=tan−1(XC+XLR)
The condition for resonance to occur
im=vm√R2+(XC−X2L)
For resonance to occur, the value of im has to be the maximum.
The value of im will be the maximum when
XC=XL
1ωC=ωL
ω2=1√LC
2πf=12π√LC
Power factor =cosϕ
Where, cosϕ=RZ=R√R2+(XC−XL)2
(i)Conditions for maximum power factor (i.e., cosϕ=1)
⋅XC=XL
Or
⋅R=0
(ii)Conditions for minimum power factor
⋅ When the circuit is purely inductive
⋅ When the circuit is purely capacitve
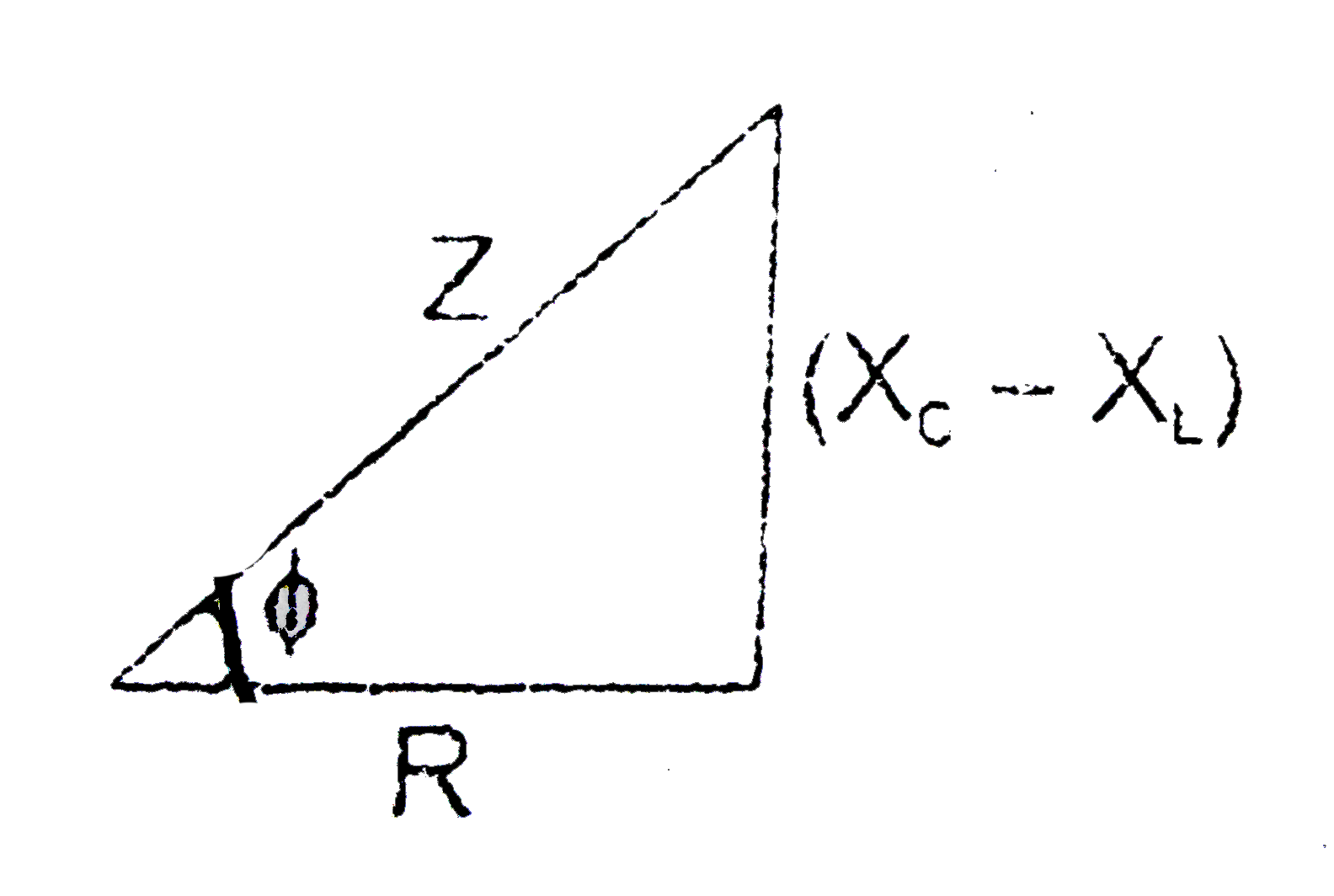
Topper's Solved these Questions
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:A.L.P
Explore 10 Videos
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:EXAMPLE
Explore 40 Videos
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:Exercise -3 Part-2
Explore 3 Videos
- ATOMIC PHYSICSBook:RESONANCE ENGLISHChapter:ATOMIC PHYSICSExercise:Advanved level problems
Explore 17 Videos
Similar Questions
A series R-L circuit is subjected to an alternating voltage given as (v=v0sinωt). Then the variation of peak current (i) with frequency (v) is denoted by
View SolutionIn a series LCR circuit connected to an ac source of variable frequency and voltage v=vmsinωt, draw a plot showing the variation of current (I) with angular frequency (ω) for two different values of resistance R1andR2(R1>R2). Write the condition under which the phenomenon of resonance occurs. For which value of the resistance out of the two curves, a sharper resonance is produced ? Define Q-factor of the circuit and give its significance.
View Solution
Knowledge Check
An ac source of voltage V=Vmsinωt is connected across the resistance R as shown in figure. The phase relation between current and voltage for this circuit is
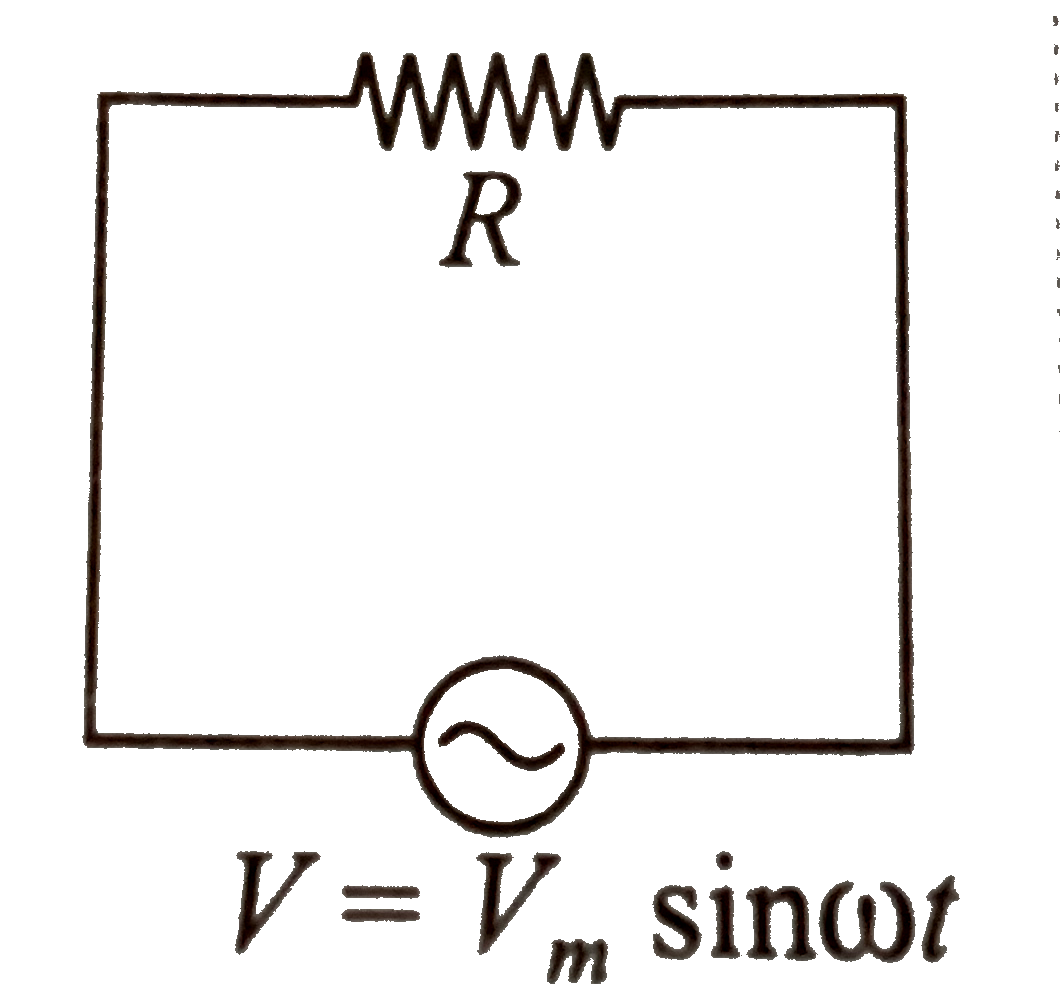 Aboth are in phaseBboth are out of phase by 90∘Cboth are out of phase by 120∘Dboth are out of phase by 180∘
Aboth are in phaseBboth are out of phase by 90∘Cboth are out of phase by 120∘Dboth are out of phase by 180∘
(a) Draw graphs showing the variations of inductive reactnace and capacitive reactance with frequency of the applied ac source .
(b) Draw the phasor diagram for a series RC circuit connected to an ac source.
(c ) An alternating voltage of 220 V is applied across a device X , a current of 0.25 A flows , which lag behind the applied voltage in phase by π2 radian . If the same voltage is applied across another device Y , the same current flows but now it is in phase with the applied voltage .
(i) Name the devices X and Y.
(ii) Calculate the current flowing in the circuit when the same voltage is applied across the series combination of X and Y.

View SolutionAn LCR circuit is connected to a source of alternating current. At resonance, the applied voltage and the current flowing through the circuit will have a phase difference of
View SolutionDerive the expression for the average power disspated in a series LCR circuit for an ac source of a voltage, v=vmsinωt, carrying a current, i=imsin(ωt+ϕ).
Hence, define the term ''Wattless current''. State under what condition it can be realized in a circuit.
View SolutionIn an AC series circuit, the instanctaneous current is zero when the instantaneous voltage is xamimum. Connected to the source may be a
View Solution(a) In a series LCR circuit connected across an AC source of variable frequency, obtain the expression for its impedance and draw a plot showing its variation with frequency of the AC source.
(b) What is the phase difference between the voltages across inductor and the capacitor at resonance in the LCR circuit ?
(c ) When and inductor is connected to a 200 V DC voltage, a current of 1Aflows trough it. when the same inductor is connected to a 200 V, 50 Hz AC source, only 0.5 A current flows. Explain, why ? Also, calculate the self inductance of the inductor.
View SolutionAn ac source of emf V=V0sinωt is connected to a capacitor of capacitance C. Deduce the expression for the current (I) flowing in it. Plot the graph of (i) Vvs.ωt,and (ii) Ivs.ωt
View SolutionAn LCR series circuit is connected to an oscillator (AC supply) having RMS voltage 200 V. If the RMS voltages across resistor, inductor and capacitor are equal, then RMS voltage across the resistor would be
View Solution

