Derive the expression for the average power disspated in a series LCR circuit for an ac source of a voltage, v=vmsinωt, carrying a current, i=imsin(ωt+ϕ).
Hence, define the term ''Wattless current''. State under what condition it can be realized in a circuit.
To derive the expression for the average power dissipated in a series LCR circuit with an AC source, we start with the given voltage and current equations.
Step 1: Write the expressions for voltage and current
The voltage across the circuit is given by:
v=Vmsin(ωt)
The current through the circuit is given by:
i=Imsin(ωt+ϕ)
Step 2: Calculate the instantaneous power
The instantaneous power P(t) can be expressed as the product of voltage and current:
P(t)=v⋅i=Vmsin(ωt)⋅Imsin(ωt+ϕ)
Step 3: Use the trigonometric identity
To simplify the product of the sine functions, we can use the trigonometric identity:
sinAsinB=12(cos(A−B)−cos(A+B))
Applying this identity:
P(t)=VmIm⋅12(cos(ϕ)−cos(2ωt+ϕ))
Step 4: Simplify the expression
Thus, we can rewrite the instantaneous power as:
P(t)=VmIm2cos(ϕ)−VmIm2cos(2ωt+ϕ)
Step 5: Calculate the average power
To find the average power Pavg over one complete cycle, we need to average P(t):
Pavg=1T∫T0P(t)dt
Where T is the time period of the AC signal. The average of the cosine term over a complete cycle is zero:
∫T0cos(2ωt+ϕ)dt=0
Thus, we have:
Pavg=VmIm2cos(ϕ)
Step 6: Express in terms of RMS values
Using the definitions of RMS values:
Vrms=Vm√2
Irms=Im√2
We can rewrite the average power as:
Pavg=VrmsIrmscos(ϕ)
Conclusion
The expression for the average power dissipated in a series LCR circuit is:
Pavg=VrmsIrmscos(ϕ)
Wattless Current
Definition: Wattless current is the component of the current in an AC circuit that does not contribute to the average power consumed. This occurs when the current is out of phase with the voltage by 90 degrees (i.e., ϕ=90∘).
Condition: Wattless current can be realized in a circuit when the circuit is purely reactive, such as in a purely inductive or purely capacitive circuit, where the phase difference between voltage and current is 90∘. In this case, the average power consumed is zero, leading to the concept of wattless current.
The voltage across the circuit is given by:
v=Vmsin(ωt)
The current through the circuit is given by:
i=Imsin(ωt+ϕ)
The instantaneous power P(t) can be expressed as the product of voltage and current:
P(t)=v⋅i=Vmsin(ωt)⋅Imsin(ωt+ϕ)
To simplify the product of the sine functions, we can use the trigonometric identity:
sinAsinB=12(cos(A−B)−cos(A+B))
Applying this identity:
P(t)=VmIm⋅12(cos(ϕ)−cos(2ωt+ϕ))
Thus, we can rewrite the instantaneous power as:
P(t)=VmIm2cos(ϕ)−VmIm2cos(2ωt+ϕ)
To find the average power Pavg over one complete cycle, we need to average P(t):
Pavg=1T∫T0P(t)dt
Where T is the time period of the AC signal. The average of the cosine term over a complete cycle is zero:
∫T0cos(2ωt+ϕ)dt=0
Thus, we have:
Pavg=VmIm2cos(ϕ)
Using the definitions of RMS values:
Vrms=Vm√2
Irms=Im√2
We can rewrite the average power as:
Pavg=VrmsIrmscos(ϕ)
The expression for the average power dissipated in a series LCR circuit is:
Pavg=VrmsIrmscos(ϕ)
Definition: Wattless current is the component of the current in an AC circuit that does not contribute to the average power consumed. This occurs when the current is out of phase with the voltage by 90 degrees (i.e., ϕ=90∘).
Topper's Solved these Questions
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SECTIONS-E
Explore 4 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SECTIONS-D
Explore 4 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SECTIONS-B
Explore 4 Videos
- SAMPLE PAPER 2019Book:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
(a) Deriver and expression for the average power consumed in a series LCR circuit connected to a.c., source in which the phase different between the voltage and the current in the circuit is ϕ.
(b) Define the quality factor in an a.c. circuit. Why should the quality factor have high value in receiving circuits ? Name the factors on which it depends.
View SolutionThe voltage and current in a series AC circuit are given by V=V0cosωtandI=i0sinωt.
What is the power dissipated in the circuit?
View Solution
Knowledge Check
An ac source of voltage V=Vmsinωt is connected across the resistance R as shown in figure. The phase relation between current and voltage for this circuit is
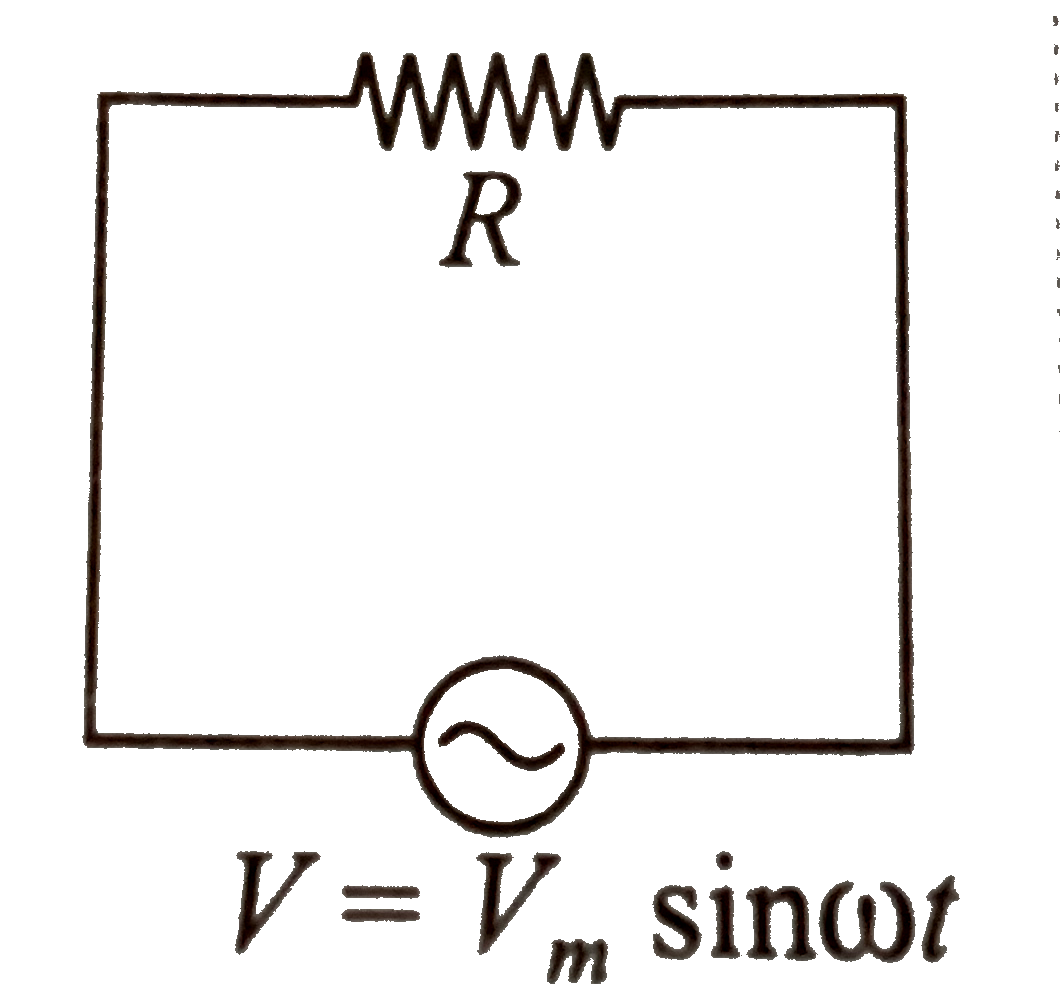 Aboth are in phaseBboth are out of phase by 90∘Cboth are out of phase by 120∘Dboth are out of phase by 180∘
Aboth are in phaseBboth are out of phase by 90∘Cboth are out of phase by 120∘Dboth are out of phase by 180∘
A 6 V, 12 W lamp is connected in series with a resistor R and a source of voltage 12 V.
What is the current flowing through the circuit?
View SolutionA series R-L circuit is subjected to an alternating voltage given as (v=v0sinωt). Then the variation of peak current (i) with frequency (v) is denoted by
View SolutionIn a series LCR circuit, an alternating emf (V) and current (I) are given by the equation V=V0sinωt,I=I0sin(ωt+π3) The average power dissipated in the circuit over a cycle of AC is
View SolutionA device X is connected across an ac source of voltage V=V0sinωt. The current throught X is given as I=I0sin(ωt+π2)
(a) Identify the device X and write the expression for its reactance.
(b) Draw graph showing variation of voltage and current with time over one cycle of ac, for X.
How does the reactance of the device X vary with frequency of the ac? Show this variation graphically.
(d) Draw the phasor diagram for the device X.
View SolutionIn any AC circuit the emf (e) and the current (i) at any instant are given respectively by e=V0sinωt
i=I0sin(ωt−ϕ)
The average power in the circuit over one cycle of AC is
View SolutionThe r.m.s current in an AC circuit is 2A. If the wattless current be √3A, what is the power factor?
View Solution(i) Find the value of the phase difference between the current and the voltage in the series LCR circuit shown below. Which one leads in phase : current or voltage ?

(ii) What making any other change, find the value of the additional capacitor C, to be connected in parallel with the capacitor C, in order to make the power factor of the circuit unity.
View Solution

