Two thin concentric and coplanar spherical shells, of radii a and b (b>a) carry charges, q and Q, respectively. Find the magnitude of the electric field at a point distant x, from their common center for 3
(i) 0<x<a (ii) a≤x<b (iii) b≤x<∞
To solve the problem, we will use Gauss's Law, which states that the electric flux through a closed surface is proportional to the charge enclosed by that surface. The electric field can be determined for three different regions based on the distance x from the center of the spherical shells.
1. Identify the Regions:
- We need to find the electric field for three different cases based on the distance x:
- Case (i): 0<x<a
- Case (ii): a≤x<b
- Case (iii): b≤x<∞
2. Case (i): 0<x<a:
- In this region, the point is inside the inner shell (radius a).
- According to Gauss's Law, since there is no charge enclosed within this region, the electric field E is given by:
E=0
3. Case (ii): a≤x<b:
- Here, the point is outside the inner shell but inside the outer shell.
- We consider a Gaussian surface (a sphere of radius x) that encloses the charge q of the inner shell.
- By Gauss's Law:
∮E⋅dA=qϵ0
- The left side becomes E⋅4πx2:
E⋅4πx2=qϵ0
- Solving for E:
E=q4πϵ0x2
4. Case (iii): b≤x<∞:
- In this case, the point is outside both shells.
- The total charge enclosed by the Gaussian surface is q+Q.
- Again using Gauss's Law:
∮E⋅dA=q+Qϵ0
- The left side becomes E⋅4πx2:
E⋅4πx2=q+Qϵ0
- Solving for E:
E=q+Q4πϵ0x2
Summary of Results:
- For 0<x<a:
E=0
- For a≤x<b:
E=q4πϵ0x2
- For b≤x<∞:
E=q+Q4πϵ0x2
- We need to find the electric field for three different cases based on the distance x:
- Case (i): 0<x<a
- Case (ii): a≤x<b
- Case (iii): b≤x<∞
- In this region, the point is inside the inner shell (radius a).
- According to Gauss's Law, since there is no charge enclosed within this region, the electric field E is given by:
E=0
- Here, the point is outside the inner shell but inside the outer shell.
- We consider a Gaussian surface (a sphere of radius x) that encloses the charge q of the inner shell.
- By Gauss's Law:
∮E⋅dA=qϵ0
- The left side becomes E⋅4πx2:
E⋅4πx2=qϵ0
- Solving for E:
E=q4πϵ0x2
- In this case, the point is outside both shells.
- The total charge enclosed by the Gaussian surface is q+Q.
- Again using Gauss's Law:
∮E⋅dA=q+Qϵ0
- The left side becomes E⋅4πx2:
E⋅4πx2=q+Qϵ0
- Solving for E:
E=q+Q4πϵ0x2
- For 0<x<a:
E=0
- For a≤x<b:
E=q4πϵ0x2
- For b≤x<∞:
E=q+Q4πϵ0x2
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTIONS-E
4 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTIONS-D
4 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTIONS-B
4 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Three concentric conducting spherical shells of radii R, R2 and 3R carry charges Q,-2Q and 3Q, respectively compute the electric field at r=52R

View SolutionThree concentric conducting spherical shells of radii R,2R carry charges Q, -2Q and 3Q, respectively. Find the electric potential at r = R and at r = 3 R, where r is the radii distance from the centre.

View SolutionTwo concentric conducting thin shells of radius R and 2 R carry charges +Q and +3Q respectively. The magnitude of electric field at a distance x outside and inside from the surface of outer sphere is same. Then the value of x is

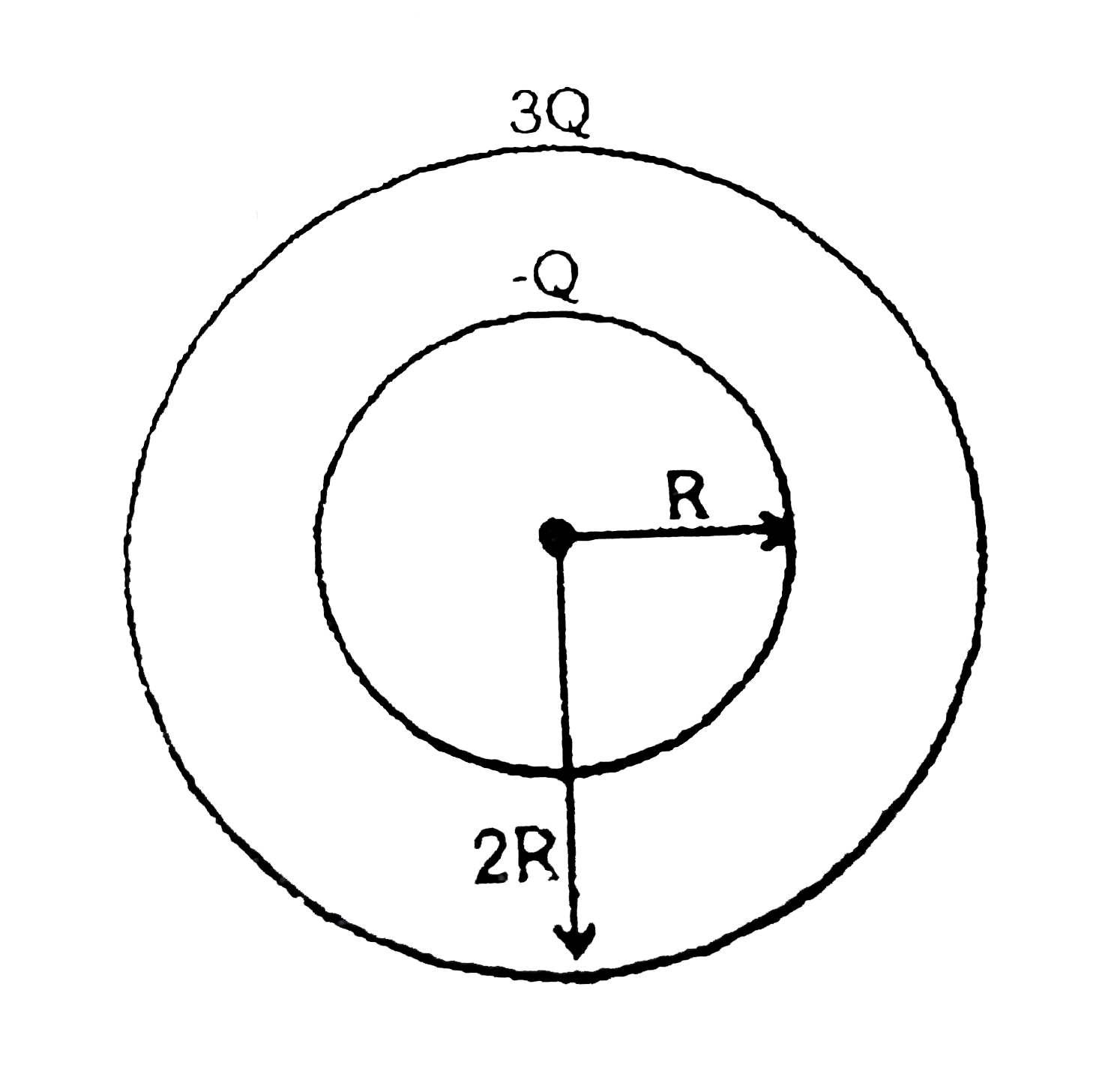
View SolutionTwo conducting hollow spherical shells of radius R and 2R carry charges -Q and 3Q respectively. How much charge will flow into the earth if inner shell is grounded?
View SolutionTwo concentric spherical conducting shells of radii r and R (r<R) carry charges q and Q respectively . The two shells are now connected by a conducting wire. The final charge on the inner shell is
View SolutionTwo concentric spherical conducting shells of radii R and 2R are carrying charges q and 2q, respectively. Both are now connected by a conducting wire. Find the change in electric potential (inV) on the outer shell.
View SolutionThere are two thin concentric conducting shells of radii a and b(a<b) . Equal charges Q given to each shell. Find the charge distribution on the inner and outer shell.
View SolutionThree concentric conducting spherical shells of radii R,2R and 3R carry charges Q,−2Q and 3Q, respectively.
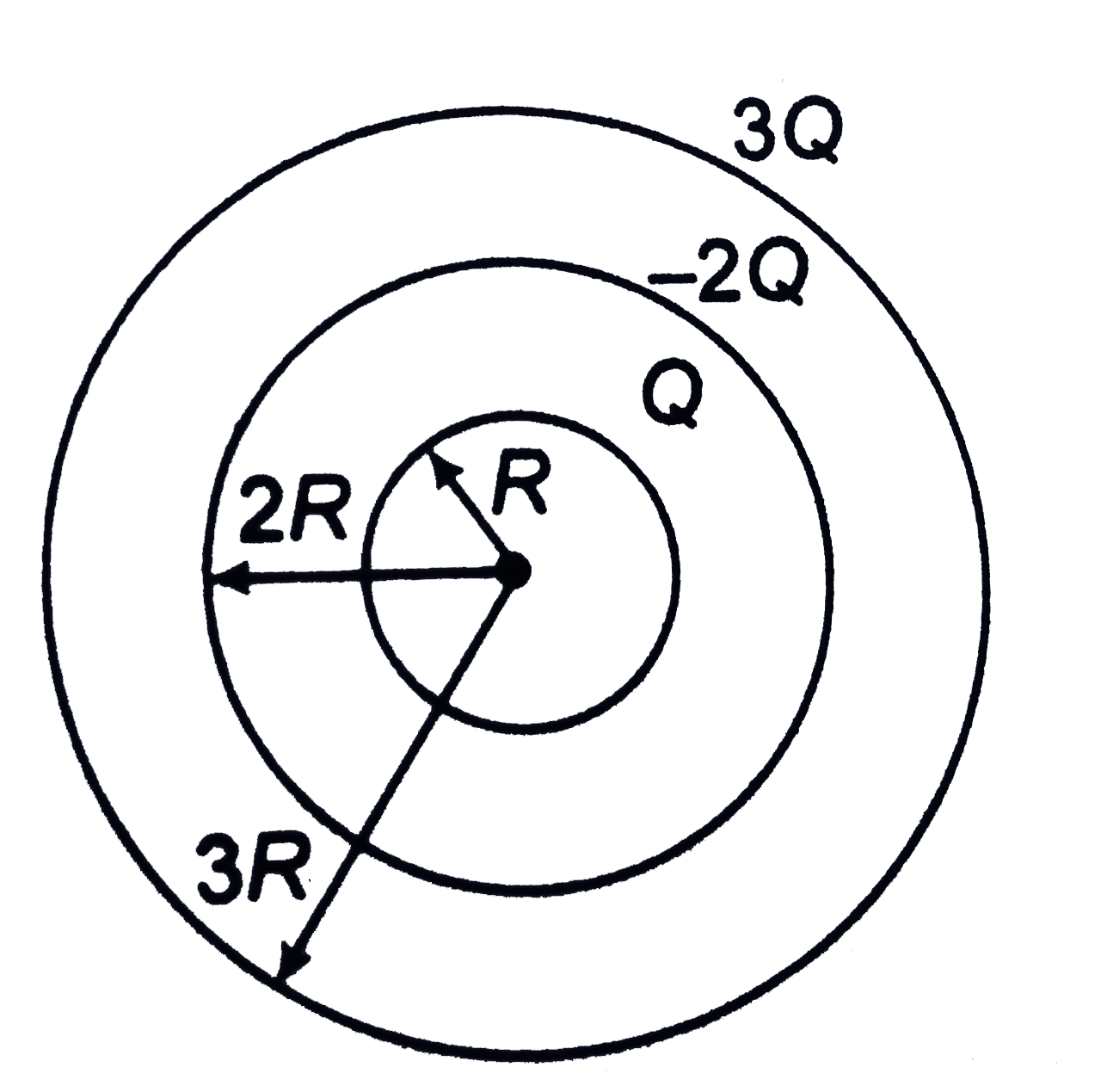
a. Find the electric potential at r=R and r=3R where r is the radial distance from the centre . b. Compute the electric field at r=52R
c. Compute the total electrostatic energy stored in the system.
The inner shell is now connected to the external one by a conducting wire, passing through a very small hole in the middle shell.
d. Compute the charges on the spheres of radii R and 3R.
e. Compute the electric field at r=52R
View SolutionTwo concentric spherical shells of radius R1 and R2(R2>R1) are having uniformly distributed charges Q1 and Q2 respectively. Find out total energy of the system.

View SolutionA conducting shell of radius R carries charge −Q. A point charge +Q is placed at the centre. The electric field E varies with distance r (from the centre of the shell) as
View Solution