The average value of current i=Imsinωtomt=π2ω to t=3π2ω si how many times of (Im)?
Video Solution
Text Solution
lrms= ⎷πω∫0I2msin2ωtdt(πω)=√I2m2=Im√2 , (ii)<i>= ⎷3π2ω∫π2ωI2msin2ωtdtπω=√I2m2=Im√2
|
Similar Questions
Knowledge Check
The voltage over a cycle varies as
V=V0sinωt for 0≤t≤πω
=−V0sinωt for πω≤t≤2πω
The average value of the voltage one cycle isAV0√2BV02CzeroD2V0π
The average value of alternating current I=I0sinωt in time interval [0,πω] is
View SolutionIf i1=3sinωtand(i2)=4cosωt, then (i3) is

View SolutionThe voltage over a cycle varies as
V=V0sinωt for 0≤t≤πω
=−V0sinωt for πω≤t≤2πω
The average value of the voltage one cycle is
View SolutionFind the rms value of current from t=0 to t=2πω if the current varies as i=Imsinωt.
View SolutionFind the rms value of current from t=0 to t=2πω if the current avries as i=Imsinωt.
View SolutionFind the rms value of current from t=0 to t=2πω if the current avries as i=Imsinωt.
View SolutionIn y= A sin ωt + A sin (ωt+(2π)/3) match the following table.
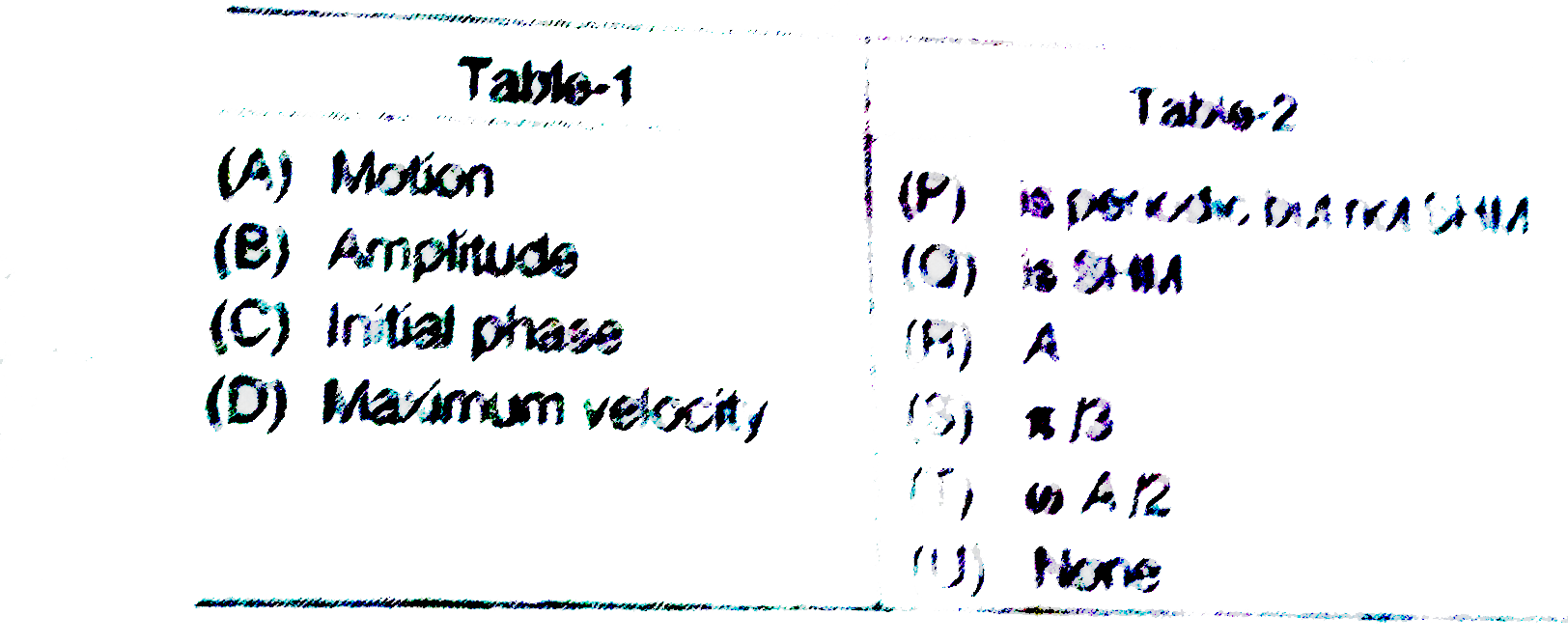
View Solution
