If i1=3sinωtand(i2)=4cosωt, then (i3) is

5sin(ωt+53∘)
5sin(ωt+37∘)
5sin(ωt+45∘)
5sin(ωt+35∘)
The correct Answer is:A
(i3)=(i1)+(i2)=3sinωt+4cosωt
=3sinωt+4sin(ωt+90∘)
(i30)=√I210+I220=√32+42=5
tan(ϕ)=43⇒ϕ=53∘
so, (i_3)=(I_(30) sin(omega t+phi)=5 sin (omega t+53^(@)).

Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Multiple Correct5videos
ALTERNATING CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Assertion-reasoning7videos
ALTERNATING CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Subjective15videos
ALTERNATING CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.315videos
ATOMIC PHYSICS
Similar Questions
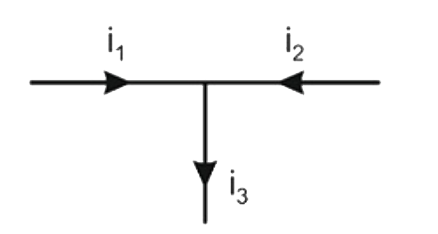
In the given figure, if i1=3sinωtandi2=4cosωt, then i3 is
 View Solution
View SolutionTwo particle AandB execute simple harmonic motion according to the equation y1=3sinωt and y2=4sin[ωt+(π/2)]+3sinωt. Find the phase difference between them.
View Solutionx1=3sinωt , x2=4cosωt. Find (i) amplitude of resultant SHM, (ii) equation of the resultant SHM.
View Solutionx1=3sinωt,x2=4cosωt
Find (i) amplitude of resultant SHM, (ii) equation of the resultant SHM.View Solutionx1=3sinωt⇒x2=4cosωt. Find (i) amplitude of resultant SHm, (ii) equation of the resultant SHm.
View SolutionThe displacement of two interfering light waves are y1=4sinωt and y2=3cos(ωt). The amplitude of the resultant waves is (y1 and y2 are in CGS system)
View SolutionWhen two displacement represented by y1=asin(ωt) and y2=bcos(ωt) are superimposed, the motion is
View SolutionStatement-1 : The superposition of the waves y1=Asin(kx−ωt) and y2=3Asin(kx+ωt) is a pure standing wave plus a travelling wave moving in the negative direction along X-axis
Statement-2 : The resultant of y1 & y2 is y=y1+y2=2Asinkxcosωt+2Asin(kx+ωt).View SolutionThe emf and current in a circuit are such that E=E0sinωt and I=I0sin(ωt−θ). This AC circuit contains
View SolutionFind the resultant amplitude and the phase difference between the resultant wave and the first wave , in the event the following waves interfere at a point , y1=(3cm)sinωt,
y2=(4cm)sin(ωt+π2),y3=(5cm)sin(ωt+π)View Solution