A capacitor of 10(μ)F and an inductor of 1 H are joined in series. An ac of 50 Hz is applied to this combination. What is the impedance of the combination?
5(π2−5)πΩ
10(10−π2)πΩ
10(π2−5)πΩ
5(10−π2)πΩ
The correct Answer is:B
To solve the problem of finding the impedance of a series combination of a capacitor and an inductor connected to an AC source, we will follow these steps:
Step 1: Calculate the inductive reactance (X_L)
The inductive reactance XL is given by the formula:
XL=ωL
where ω=2πf and L is the inductance.
Given:
- f=50Hz
- L=1H
Calculating ω:
ω=2π×50=100πrad/s
Now substituting into the formula for XL:
XL=100π×1=100πΩ
Step 2: Calculate the capacitive reactance (X_C)
The capacitive reactance XC is given by the formula:
XC=1ωC
Given:
- C=10μF=10×10−6F
Substituting the values:
XC=12π×50×10×10−6
Calculating:
XC=1100π×10−6=1000πΩ
Step 3: Calculate the total impedance (Z)
The total impedance Z of a series circuit containing an inductor and a capacitor is given by:
Z=√(XL−XC)2
Substituting the values of XL and XC:
Z=√(100π−1000π)2
To simplify:
1. Find a common denominator:
Z=√(100π2−1000)2/π2
2. Thus:
Z=1π√(100π2−1000)2
Final Result
The impedance Z can be expressed as:
Z=100(10−π2100)Ω
The inductive reactance XL is given by the formula:
XL=ωL
where ω=2πf and L is the inductance.
- f=50Hz
- L=1H
ω=2π×50=100πrad/s
XL=100π×1=100πΩ
The capacitive reactance XC is given by the formula:
XC=1ωC
- C=10μF=10×10−6F
XC=12π×50×10×10−6
Calculating:
XC=1100π×10−6=1000πΩ
The total impedance Z of a series circuit containing an inductor and a capacitor is given by:
Z=√(XL−XC)2
Z=√(100π−1000π)2
1. Find a common denominator:
Z=√(100π2−1000)2/π2
2. Thus:
Z=1π√(100π2−1000)2
The impedance Z can be expressed as:
Z=100(10−π2100)Ω
Topper's Solved these Questions
- ALTERNATING CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:ALTERNATING CURRENTExercise:Exercises Multiple Correct
Explore 5 Videos
- ALTERNATING CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:ALTERNATING CURRENTExercise:Exercises Assertion-reasoning
Explore 7 Videos
- ALTERNATING CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:ALTERNATING CURRENTExercise:Exercises Subjective
Explore 15 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:ATOMIC PHYSICSExercise:ddp.4.3
Explore 15 Videos
Similar Questions
A capacitor of 10μF and an inductor of 1 H are joined in series. An ac of 50 Hz is applied to this combination. What is the impedance of the combination?
View SolutionA resistance of 40 ohms and an inductance of 95.5 millihenry are connected in series in a 50 cycle/sec AC circuit. The impedence of this combination is very nearly
View SolutionA circuit is set up by connecting L=100mH, C=5μF and R=100Ω in series. An alternating emf of 150√2 )V,(500)/(pi) Hz is applied across this series combination.Calculate the impedance of the circuit. What is the average power dissipated in the resistor
View SolutionA 10μF capacitor is conneted with 1 henry inductance in series with a 50 hertz source of a.c. Calculate the impedance of the combination.
View SolutionAn inductance L , a capacitor of 20μF and a resistor of 10Ω are connected in series with an AC source of frequency 50 Hz . If the current is in phase with the voltage, then the inductance of the inductor is
View SolutionA capacitor, a resistor and a 40 mH inductor are connected in series to an a.c. source of frequency 60 Hz. Calculate the capacitance of the capacitor,if current is in phase with the voltage.
View SolutionAn inductance of 1 mH a condenser of 10μF and a resistance of 50Ω are connected in series. The reactances of inductor and condensers are same. The reactance of either of them will be
View SolutionCapacitors C1(10μF)andC2(20μF) are connected in series across a 3 kV supply, as shown. What is the charge on the capacitor C1 ?
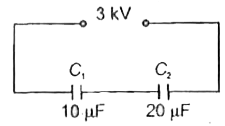
View SolutionThree capacitors each of capacitance 9 pF are connected in series. What is the total capacitance of the combination ?
View SolutionAn inductor 20×10−3 a capacitor 100(μ)F and a resistor 50Ω are connected in series across a source of emf V=10sin314t.
Then the energy dissipated in the circuit in 20 mim is
View Solution