Find the rms value of current from t=0 to t=2πω if the current avries as i=Imsinωt.
To find the RMS (Root Mean Square) value of the current given by the equation i=Imsin(ωt) from t=0 to t=2πω, we can follow these steps:
1. Understand the Definition of RMS Value:
The RMS value of a function i(t) over a period T is defined as:
IRMS=√1T∫T0i2(t)dt
where T is the time period over which we are calculating the RMS value.
2. Identify the Time Period:
For the function i(t)=Imsin(ωt), the time period T is given by:
T=2πω
3. Set Up the Integral:
We need to calculate:
IRMS=√1T∫T0(Imsin(ωt))2dt
Substituting T:
IRMS=
⎷12πω∫2πω0(Imsin(ωt))2dt
4. Simplify the Integral:
The integral can be simplified:
(Imsin(ωt))2=I2msin2(ωt)
Thus, we have:
IRMS=
⎷ω2π∫2πω0I2msin2(ωt)dt
We can factor out I2m:
IRMS=Im
⎷ω2π∫2πω0sin2(ωt)dt
5. Evaluate the Integral:
To evaluate the integral ∫2πω0sin2(ωt)dt, we use the identity:
sin2(x)=1−cos(2x)2
Thus:
∫2πω0sin2(ωt)dt=∫2πω01−cos(2ωt)2dt
This can be split into two integrals:
=12(∫2πω01dt−∫2πω0cos(2ωt)dt)
6. Calculate Each Integral:
- The first integral:
∫2πω01dt=2πω
- The second integral:
∫2πω0cos(2ωt)dt=0(since it completes a full cycle)
Therefore:
∫2πω0sin2(ωt)dt=12(2πω−0)=πω
7. Substitute Back into RMS Formula:
Now substituting back:
IRMS=Im√ω2π⋅πω=Im√12=Im√2
Final Answer:
The RMS value of the current is:
IRMS=Im√2
The RMS value of a function i(t) over a period T is defined as:
IRMS=√1T∫T0i2(t)dt
where T is the time period over which we are calculating the RMS value.
For the function i(t)=Imsin(ωt), the time period T is given by:
T=2πω
We need to calculate:
IRMS=√1T∫T0(Imsin(ωt))2dt
Substituting T:
IRMS=
⎷12πω∫2πω0(Imsin(ωt))2dt
The integral can be simplified:
(Imsin(ωt))2=I2msin2(ωt)
Thus, we have:
IRMS=
⎷ω2π∫2πω0I2msin2(ωt)dt
We can factor out I2m:
IRMS=Im
⎷ω2π∫2πω0sin2(ωt)dt
To evaluate the integral ∫2πω0sin2(ωt)dt, we use the identity:
sin2(x)=1−cos(2x)2
Thus:
∫2πω0sin2(ωt)dt=∫2πω01−cos(2ωt)2dt
This can be split into two integrals:
=12(∫2πω01dt−∫2πω0cos(2ωt)dt)
- The first integral:
∫2πω01dt=2πω
- The second integral:
∫2πω0cos(2ωt)dt=0(since it completes a full cycle)
Therefore:
∫2πω0sin2(ωt)dt=12(2πω−0)=πω
Now substituting back:
IRMS=Im√ω2π⋅πω=Im√12=Im√2
The RMS value of the current is:
IRMS=Im√2
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - SOLVED MISCELLANEOUS
14 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE SECTION A
4 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - A.L.P
10 Videos
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems
17 Videos
Similar Questions
Find the rms value of current from t=0 to t=2πω if the current varies as i=Imsinωt.
View SolutionFind the rms value of current i=Imsinωt from (i)t=0tot=πω (ii) t=π2ωtot=3π2ω
View SolutionFind the effective value of current i=2+4cos100πt.
View SolutionFind the effective value of current i=2+4cos100πt.
View Solutionr.m.s. value of current i=3+4sin(ωt+π/3) is:
View SolutionThe average value of current i=Imsinωtomt=π2ω to t=3π2ω si how many times of (Im)?
View SolutionThe average value of current i=Imsinωtomt=π2ω to t=3π2ω si how many times of (Im)?
View Solutionr.m.s. value of current i=3+4sin (omegat+pi//3) is
View SolutionIn an AC circuit, the rms value of the current Irms is related to the peak current I0 as
View SolutionFind the avarage value of current (in A) shown graphically in fig. From t=0→t=2s.
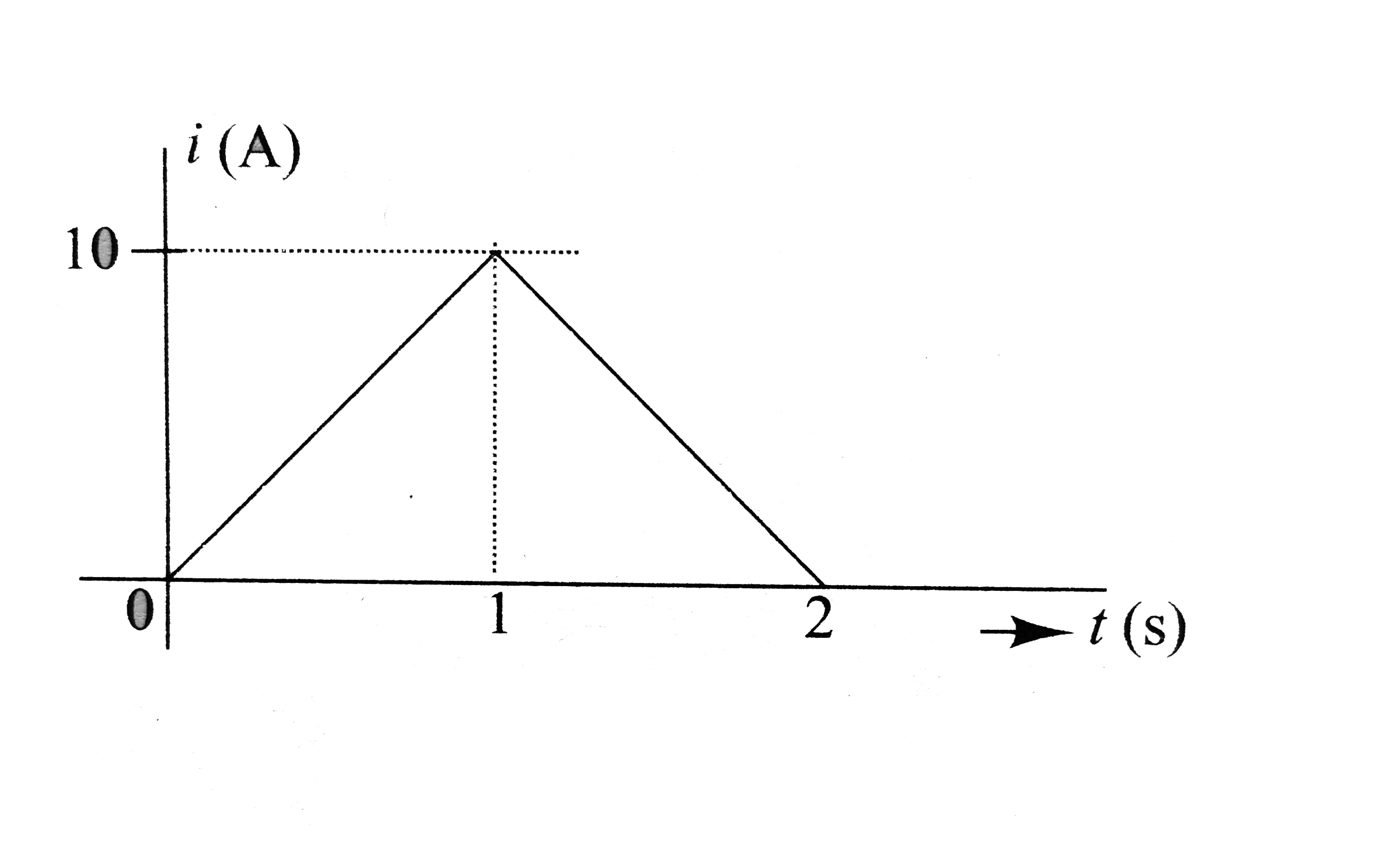 .
.
View Solution
