Find the resultant magnetic force and torque on the loop.
To find the resultant magnetic force and torque on a circular loop carrying a current in a magnetic field, we can follow these steps:
1. Understanding the Loop and Forces:
- A circular loop is considered, and we need to analyze the forces acting on it due to a magnetic field.
- The magnetic force on a segment of wire is given by the equation:
→F=I→L×→B
where I is the current, →L is the length vector of the wire segment, and →B is the magnetic field vector.
2. Net Force on the Loop:
- For a complete loop, the sum of the length vectors (→L) around the loop equals zero because they are symmetrically distributed.
- Therefore, the net magnetic force on the loop is:
→Fnet=0
3. Torque on the Loop:
- The torque (→τ) on the loop in a magnetic field is given by:
→τ=→M×→B
where →M is the magnetic moment of the loop.
4. Calculating the Magnetic Moment:
- The magnetic moment →M is calculated using the formula:
→M=nI→A
where n is the number of turns (for a single loop, n=1), I is the current, and →A is the area vector of the loop.
- The area A of a circular loop is given by:
A=πr2
- Thus, the magnetic moment becomes:
→M=Iπr2^i
(where ^i is the direction of the area vector, perpendicular to the plane of the loop).
5. Finding the Torque:
- Now substituting →M into the torque equation:
→τ=(Iπr2^i)×→B
- If the magnetic field →B is in the ^k direction (out of the plane), the magnitude of the torque can be calculated as:
|→τ|=|→M||→B|sin(θ)
- Since θ=90∘ (the angle between ^i and ^k), we have:
|→τ|=Iπr2B
Final Answers:
- Resultant Magnetic Force: →Fnet=0
- Torque: |→τ|=Iπr2B
- A circular loop is considered, and we need to analyze the forces acting on it due to a magnetic field.
- The magnetic force on a segment of wire is given by the equation:
→F=I→L×→B
where I is the current, →L is the length vector of the wire segment, and →B is the magnetic field vector.
- For a complete loop, the sum of the length vectors (→L) around the loop equals zero because they are symmetrically distributed.
- Therefore, the net magnetic force on the loop is:
→Fnet=0
- The torque (→τ) on the loop in a magnetic field is given by:
→τ=→M×→B
where →M is the magnetic moment of the loop.
- The magnetic moment →M is calculated using the formula:
→M=nI→A
where n is the number of turns (for a single loop, n=1), I is the current, and →A is the area vector of the loop.
- The area A of a circular loop is given by:
A=πr2
- Thus, the magnetic moment becomes:
→M=Iπr2^i
(where ^i is the direction of the area vector, perpendicular to the plane of the loop).
- Now substituting →M into the torque equation:
→τ=(Iπr2^i)×→B
- If the magnetic field →B is in the ^k direction (out of the plane), the magnitude of the torque can be calculated as:
|→τ|=|→M||→B|sin(θ)
- Since θ=90∘ (the angle between ^i and ^k), we have:
|→τ|=Iπr2B
- Resultant Magnetic Force: →Fnet=0
- Torque: |→τ|=Iπr2B
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - PROBLEM
12 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-1 PART-1
83 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
In Fig., a semicircular wire is placed in a uniform field →B directed towards right. Find the resultant magnetic force and torque on it.

View SolutionIn Fig., a semicircular wire is placed in a uniform field →B directed towards right. Find the resultant magnetic force and torque on it.

View SolutionIn Fig., find the resultant magnetic force and torque about C.

View SolutionA square loop of 5 cm carrying a current 0.2 A in the clockwise direction is placed at a distance of 10 cm from an infinity long wire carrying a current of 1 A as shown. Calculate (i) the resultant magnetic force and (ii) the torque, if any, acting on the loop.
View SolutionFind resultant magnetic field at C in Fig
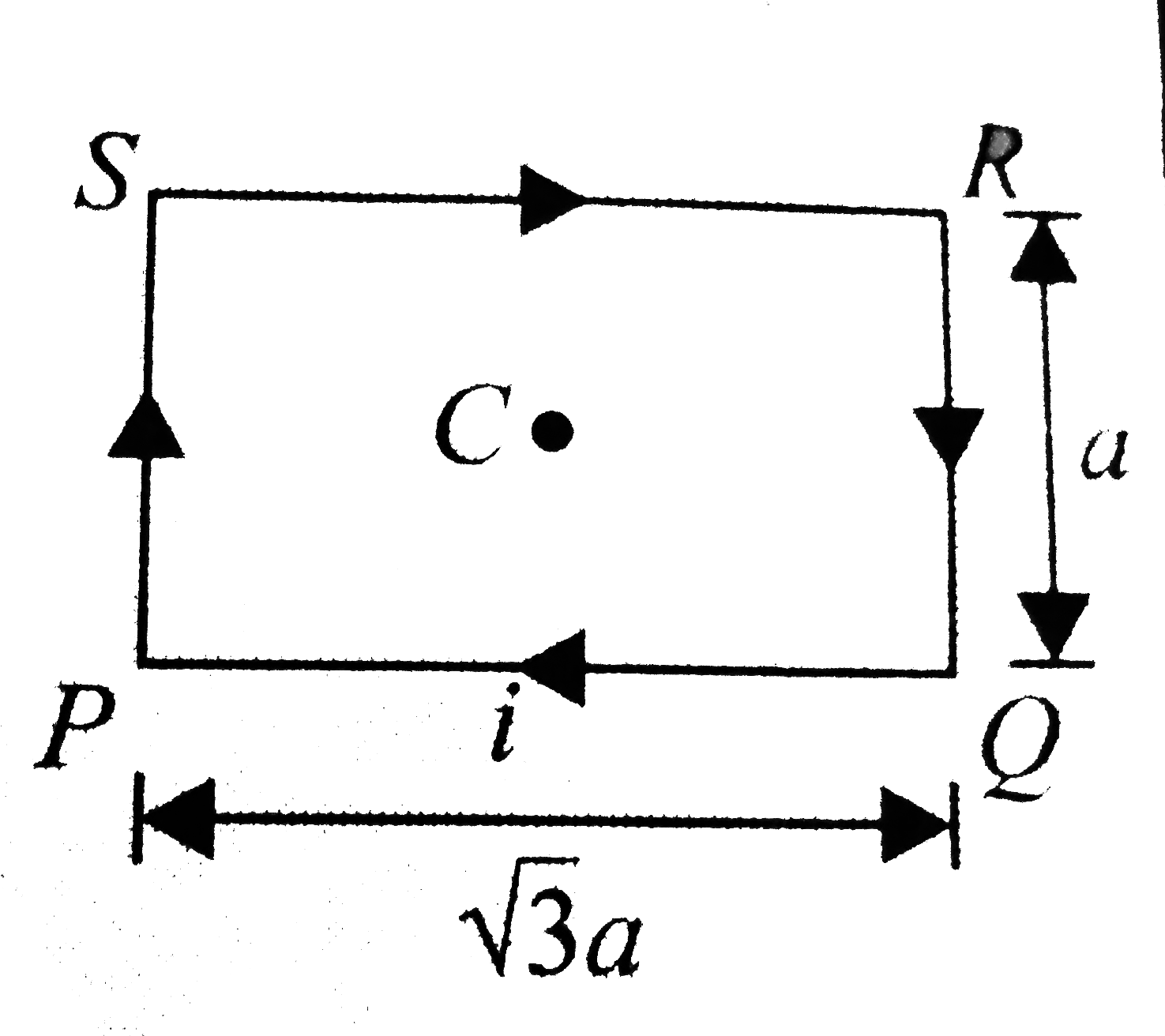
View SolutionFind resultant magnetic field at C in Fig

View SolutionThe magnetic field existing in a region is given by ,B=B0(xL+x2L2)ˆk.A square loop edge L carrying a current I is placed with its parallel to the X and Y-axis Find the net magnetic force experienced by the loop
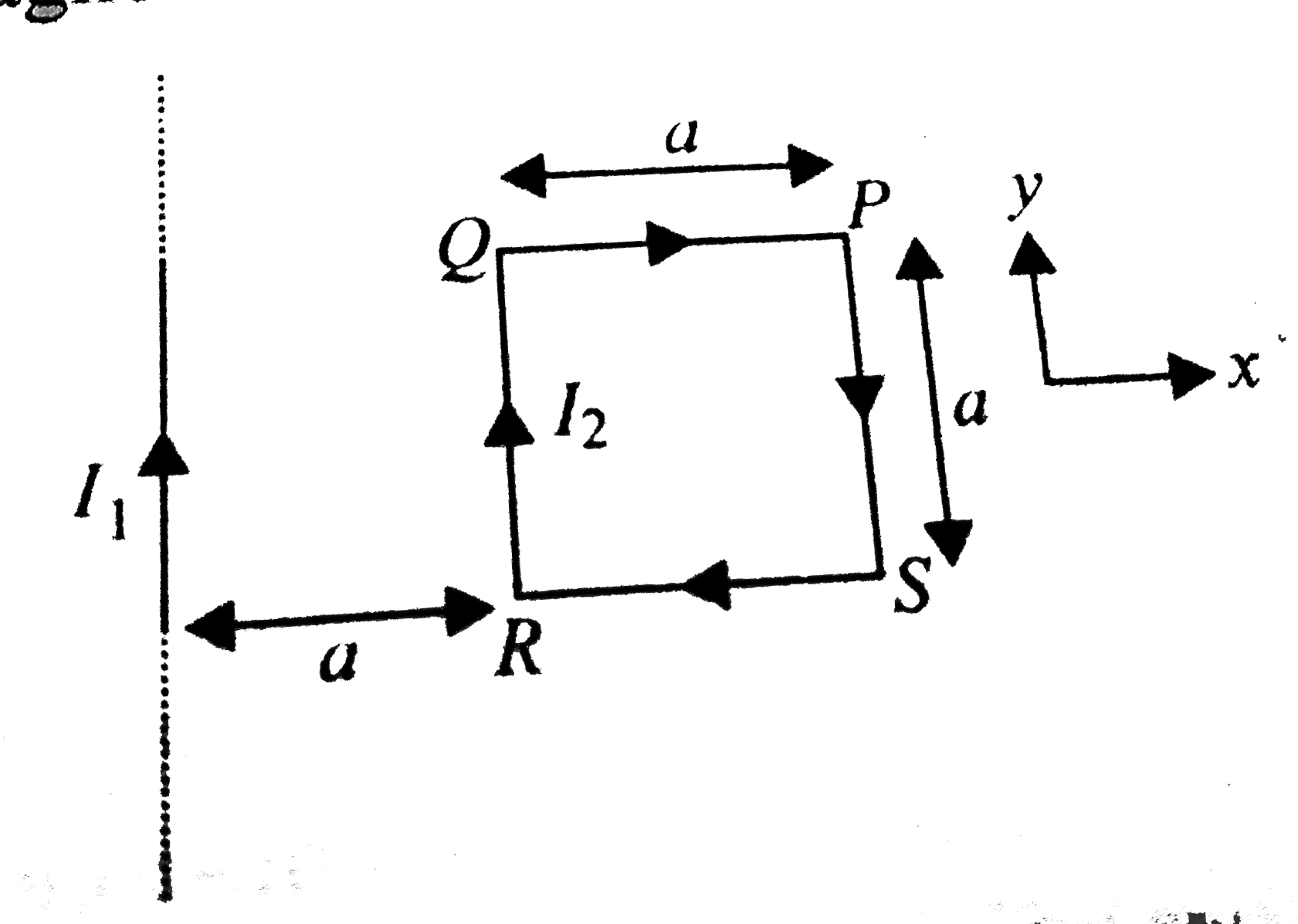
View SolutionFind the magnetic force on loop PQRS due to the wire.
View SolutionIf several forces act on a particle, the total torque on the particle mauy be obtained by first finding the resultant force and then taking torque of this resultant. Prove this. Is this result valid for the forces actin on difeent partivles of a body in such a way that their lines of acting intersect at a common point?
View SolutionA current loop of arbitrary shape lies in a uniform magnetic field B. show that the net magnetic force acting on the loop is zero.
View Solution
