A whistle of frequency 540 Hz is moving in a circle of radius 2 ft at a constant angular speed of 15 rad/s. What are the lowest and highest frequencies heard by a listener standing at rest, a long distance away from the centre of the circle? (Velocity of sound in air is 1100ft/s)
The whistle is moving along a circular path with constant angular velocity ω. The linear velocity of the whistie is given by
vS=ωR
where, R is radius of the circle.

At point A and B, the velocity vS of whistle is parallel to line OP, i.e., with respect to observer at P. whistle has maximum velocity vs away from P at point A, and towards P at point B. (Since distance OP is large compared to radius R, whistle may be assumed to be moving along line OP).
Observer, therefore, listens maximum frequency when source is at B moving towards observe:
fmax=f(v)v−vs
where, v is speed of sound in air. Similarly, observer listens minimum frequency when source is at A, moving away from observer:
fmin=f(v)v+vs
For f=540Hz,vs=2ft×15rad/s=30ft/s. and v=1100ft/s.
we get (approx.) fmax=555Hz and fmin=525Hz.
Topper's Solved these Questions
- SOUND WAVESBook:RESONANCE ENGLISHChapter:SOUND WAVESExercise:Board Level Exercise
Explore 33 Videos
- SOUND WAVESBook:RESONANCE ENGLISHChapter:SOUND WAVESExercise:Exercise- 1 PART - I
Explore 34 Videos
- SOUND WAVESBook:RESONANCE ENGLISHChapter:SOUND WAVESExercise:Exercise- 3 PART - I
Explore 47 Videos
- SIMPLE HARMONIC MOTIONBook:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Exercise
Explore 28 Videos
- STRING WAVESBook:RESONANCE ENGLISHChapter:STRING WAVESExercise:Exercise
Explore 32 Videos
Similar Questions
A whitle of frequency 540 Hz rotates in a horizontal circle of radius 2 m at an angular speed of 15rads. What is the lowest and the highest frequency heard by a listener a long distance away at rest with respect to the centre of the circle? (Velocity of sound in air is c=330ms.)
View SolutionA whistle of frequency 500 Hz is rotated in a circle of radius cne metre with an angular speed of 10 radian/sec. Calculate the lowest and the highest frequency heard by a listener at a long distance away at rest with respect to the centre of the circle ? (Velocity of sound = 340m/s)
View SolutionA whistle of frequency 540HZ rotates in a circle of radius 2mat a linear speed of 30m/s . What is the lowest and highest frequency heard by an observer a long distance away at rest with respect to the centre of circle ? Take speed of sound of sound in air as 330m/s. Can the apparent frequency be ever equal to actual ?
View SolutionA whistle 'S' of frequency v revolves in a circle of radius R at a constant speed v. what is the ratio of the largest and smallest frequency detected by a detector D, at rest, at a distance 2 R from the centre of the circle as shown in the figure? (take speed of sound in air as c)
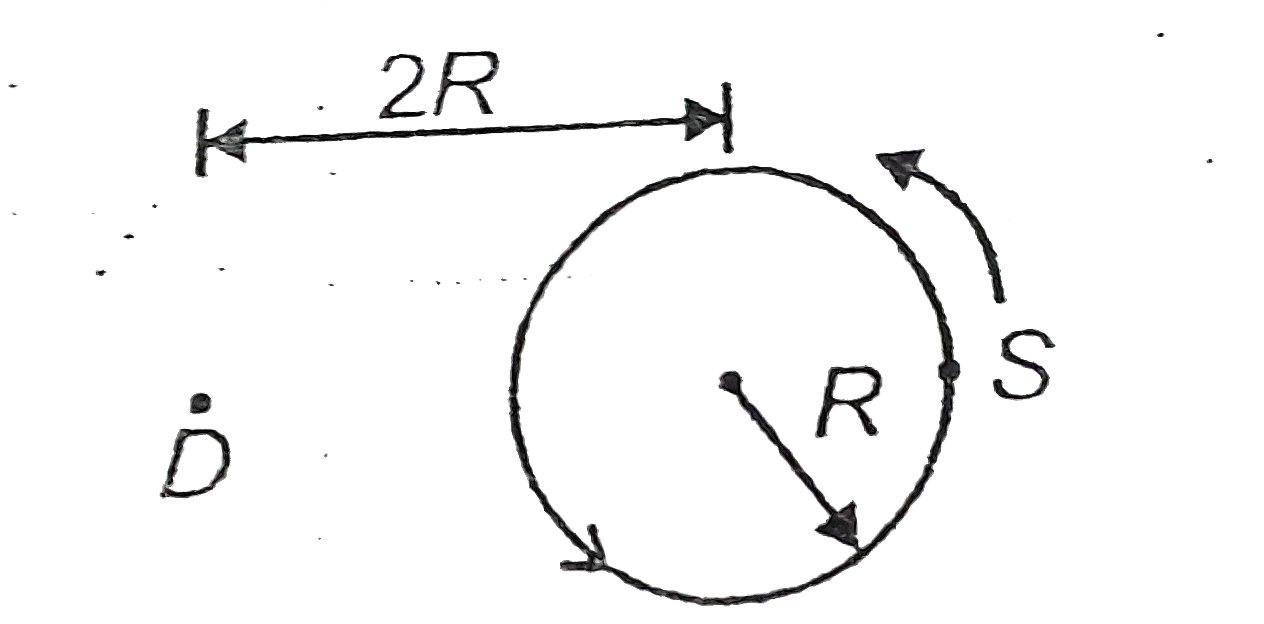
View SolutionA small source of sound vibrating frequency 500 Hz is rotated in a circle of radius 100π cm at a constant angular speed of 5.0 revolutions per second. The speed of sound in air is 330ms.
Q. For an observer who is at rest at a great distance from the centre of the circle but nearly in the same plane, the minimum fmin and the maximum fmax of the range of values of the apparent frequency heard by him will be
View SolutionA small source of sound vibrating frequency 500 Hz is rotated in a circle of radius 100π cm at a constant angular speed of 5.0 revolutions per second. The speed of sound in air is 330ms.
Q. For an observer who is at rest at a great distance from the centre of the circle but nearly in the same plane, the minimum fmin and the maximum fmax of the range of values of the apparent frequency heard by him will be
View SolutionA whistle emitting a sound of frequency 440Hz is tied to a string of 1.5m length and roated with an angular velocity of 20rad/s in the horizontal plane. Calculate the range of frequencies heard by an observer stationed at a larger distance from the whistle .(Speed of sound =330m/s) .
View SolutionA small source of sound vibrating at frequency 500 Hz is rotated in a circle of radius 1002π cm at a constant angular speed of 5-0 revolutions per second. A listener situates himself in the plane of the circle. Find the minimum and the maximum frequency of the sound observed. Speed of sound in air =332ms−1.
View SolutionA man is travelling in a train towards the station with a speed of 50 m/s. calculate the apparent frequency heard by him of whistle which is blown at the station with a frequency 200 Hz. Velocity of sound in air is 350 m/s.
View SolutionA car blowing a horn of frequency 350 Hz is moving normally towards a wall a speed of 5 m/s The beat frequency heard by a person standing between the car and wall is (speed of sound in air =350 m/s )
View Solution

