A circular plate of area 0.4cm2 is kept at distance of 2m source of power πW. Find the amount of energy received by plate in 5 secs.
To solve the problem step by step, we will follow the instructions given in the video transcript.
Step 1: Identify the given values
- Area of the circular plate, A=0.4cm2
- Distance from the source, d=2m
- Power of the source, P=πW
- Time duration, T=5s
Step 2: Calculate the total energy emitted by the source
The energy emitted by the source can be calculated using the formula:
E=P×T
Substituting the values:
E=πW×5s=5πJ
Step 3: Calculate the energy received at a distance of 2 meters
The energy spreads out in a spherical shape. The formula for energy at a distance r is given by:
Er=E4πr2
Substituting E=5πJ and r=2m:
Er=5π4π(22)=5π4π×4=5π16π
The π cancels out:
Er=516J
Step 4: Calculate the energy received by the circular plate
To find the energy received by the plate, we need to consider the area of the plate. First, convert the area from cm² to m²:
A=0.4cm2=0.4×10−4m2=4×10−5m2
Now, the energy received by the plate Ep can be calculated as:
Ep=A×Er
Substituting the values:
Ep=4×10−5m2×516J
Calculating this gives:
Ep=20×10−516=2016×10−5=1.25×10−5J
Converting this to microjoules:
Ep=12.5μJ
Final Answer
The amount of energy received by the plate in 5 seconds is 12.5μJ.
---
- Area of the circular plate, A=0.4cm2
- Distance from the source, d=2m
- Power of the source, P=πW
- Time duration, T=5s
The energy emitted by the source can be calculated using the formula:
E=P×T
Substituting the values:
E=πW×5s=5πJ
The energy spreads out in a spherical shape. The formula for energy at a distance r is given by:
Er=E4πr2
Substituting E=5πJ and r=2m:
Er=5π4π(22)=5π4π×4=5π16π
The π cancels out:
Er=516J
To find the energy received by the plate, we need to consider the area of the plate. First, convert the area from cm² to m²:
A=0.4cm2=0.4×10−4m2=4×10−5m2
Now, the energy received by the plate Ep can be calculated as:
Ep=A×Er
Substituting the values:
Ep=4×10−5m2×516J
Calculating this gives:
Ep=20×10−516=2016×10−5=1.25×10−5J
Converting this to microjoules:
Ep=12.5μJ
The amount of energy received by the plate in 5 seconds is 12.5μJ.
Topper's Solved these Questions
- SOUND WAVESBook:RESONANCE ENGLISHChapter:SOUND WAVESExercise:Board Level Exercise
Explore 33 Videos
- SOUND WAVESBook:RESONANCE ENGLISHChapter:SOUND WAVESExercise:Exercise- 1 PART - I
Explore 34 Videos
- SOUND WAVESBook:RESONANCE ENGLISHChapter:SOUND WAVESExercise:Exercise- 3 PART - I
Explore 47 Videos
- SIMPLE HARMONIC MOTIONBook:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Exercise
Explore 28 Videos
- STRING WAVESBook:RESONANCE ENGLISHChapter:STRING WAVESExercise:Exercise
Explore 32 Videos
Similar Questions
A parallel plate capacitor consist of two circular plates of area 0.04m2 each. They are separated by a distance 0.4 mm. If displacement current between the plates is 6A then rate of change in electric field between the plate w.r.t. time will be
View SolutionA circular hole of diameter 4 cm is cut out of a rectangular plate of dimension 10 cm by 8 cm. Find the area of the plate after the hole has been cut out.
View SolutionA parallel plate capacitor consists of two circular plates each of radius 2cm, separated by a distance of 0.1mm. If the potential difference across the plates is varying at the rate of 5×106Vs−1, then the value of displacement current is
View SolutionA parallel plate capacitor is constructed with plates of area 0.0280m2 and separation 0.550mm. Find the magnitude of the charge on each plate of this capacitor when the potential between the plates is 20.1V

View SolutionA parallel plate capacitor consists of two circular plates of radius R=0.1 m. they are separated by a distance d=0.5mm, if electric field between the capacitor plates changes as dEdt=5×1013Vm×s. Find displacement current between the plates.
View SolutionThe radius of a circular plate increase at the rate of 0.1 cm per second. At what rate does the area increase when the radius of plate is 5πcm?
View SolutionCharges 2q and −3q are given to two identical metal plates of area of cross section A. the distance between the plates is d. Find the capacitance and potential difference between the plates.
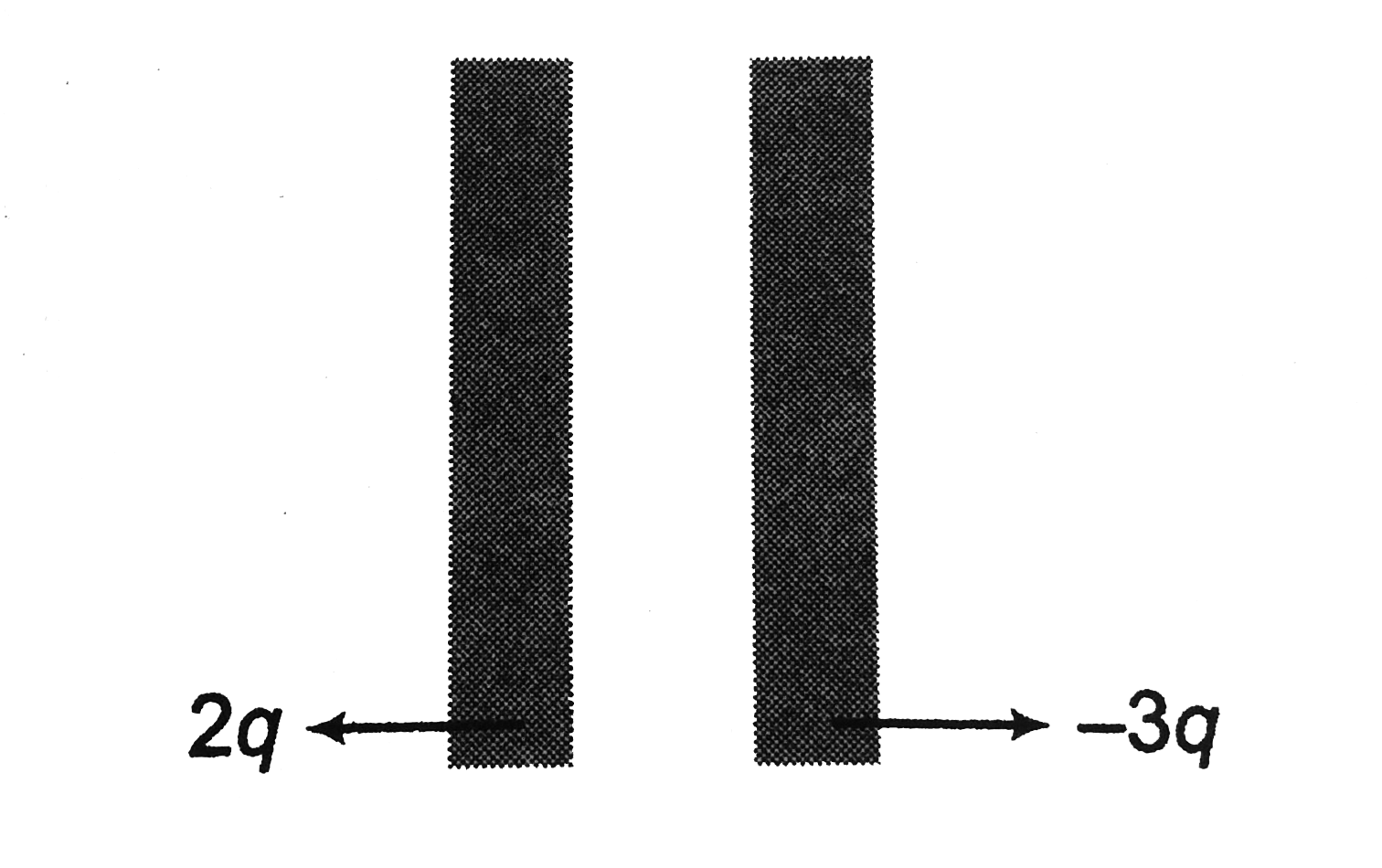
View SolutionThe plates of a parallel plate capacitance 1.0 F are separated by a distance d =1 cm. Find the plate area .
View SolutionFind the area of a circular plate of radius 1.4 m.
View SolutionBetween a plate of area 100cm2 and another plate of area 100m2 there is a 1mm, thick layer of water, if the coefficient of viscosity of water is 0.01 poise, then the force required to move the smaller plate with a velocity 10cms−1 with reference to large plate is
View Solution

