The audible frequency for a normal human being is 20Hz to 20kHz. Fuind the corresponding wavelengths if the speed of sound in air 320m/s.
(b) Find the phase difference between two position separated by 20cm at a particular instant.
The correct Answer is:16mm,16m
To solve the problem step by step, we will break it down into two parts: finding the wavelengths corresponding to the given frequencies and then calculating the phase difference between two positions separated by a specified distance.
Part (a): Finding the Wavelengths
1. Identify the Given Values:
- Speed of sound in air, v=320m/s
- Minimum audible frequency, fmin=20Hz
- Maximum audible frequency, fmax=20kHz=20×103Hz
2. Use the Wavelength Formula:
The wavelength λ can be calculated using the formula:
λ=vf
3. Calculate Wavelength for Minimum Frequency:
λ1=vfmin=320m/s20Hz=16m
4. Calculate Wavelength for Maximum Frequency:
λ2=vfmax=320m/s20×103Hz=32020000=0.016m=16×10−3m
Summary of Part (a):
- Wavelength for 20 Hz: λ1=16m
- Wavelength for 20 kHz: λ2=16×10−3m
---
Part (b): Finding the Phase Difference
1. Identify the Given Values:
- Path difference, Δx=20cm=0.2m
2. Use the Phase Difference Formula:
The phase difference Δϕ can be calculated using the formula:
Δϕ=2πλΔx
3. Calculate Phase Difference for λ1:
Δϕ1=2πλ1Δx=2π16×0.2=π40
4. Calculate Phase Difference for λ2:
Δϕ2=2πλ2Δx=2π16×10−3×0.2=2π×0.216×10−3=0.4π16×10−3=25π
Summary of Part (b):
- Phase difference for λ1: Δϕ1=π40
- Phase difference for λ2: Δϕ2=25π
---
- Speed of sound in air, v=320m/s
- Minimum audible frequency, fmin=20Hz
- Maximum audible frequency, fmax=20kHz=20×103Hz
The wavelength λ can be calculated using the formula:
λ=vf
λ1=vfmin=320m/s20Hz=16m
λ2=vfmax=320m/s20×103Hz=32020000=0.016m=16×10−3m
- Wavelength for 20 Hz: λ1=16m
- Wavelength for 20 kHz: λ2=16×10−3m
- Path difference, Δx=20cm=0.2m
The phase difference Δϕ can be calculated using the formula:
Δϕ=2πλΔx
Δϕ1=2πλ1Δx=2π16×0.2=π40
Δϕ2=2πλ2Δx=2π16×10−3×0.2=2π×0.216×10−3=0.4π16×10−3=25π
- Phase difference for λ1: Δϕ1=π40
- Phase difference for λ2: Δϕ2=25π
Topper's Solved these Questions
- SOUND WAVESBOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 1 PART - II
30 Videos
- SOUND WAVESBOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 2 PART - I
24 Videos
- SOUND WAVESBOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Board Level Exercise
33 Videos
- SIMPLE HARMONIC MOTIONBOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise
28 Videos
- STRING WAVESBOOK - RESONANCE ENGLISHCHAPTER - STRING WAVESEXERCISE - Exercise
32 Videos
Similar Questions
A sound wave of frequency 80Hz is travelling with speed 320m/s.
(a) Find the change in phase at a given position in 400ms
(b) Find the phase difference between two positions seperated by 20cm at a particular instant.
View SolutionA wave of frequency 20 Hz is propagatinig is space with speed 200 m/s. the phase difference of the two points of wave separated by a distance 5 m is
View SolutionTwo successive resonance frequencies in an open organ pipe are 1944 Hz and 2592 Hz. Find the length of the tube. The speed of sound in air is 324ms−1.
View SolutionIn stationary waves, distance between a node and its nearest antinode is 20 cm . The phase difference between two particles having a separation of 60 cm will be
View SolutionA progressive wave moves with a velocity of 36m/ s in a medium with a frequency of 200Hz. The phase difference between two particles seperated by a distance of 1 cm is
View SolutionThe angular frequency of a particle in a progressive wave in an elastic medium is 50π rad/s and it is moving with velocity of 150 m/s. The phase difference between two particles separated by a distance 30m at the same instant will be
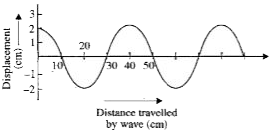
View SolutionA wave travelling along the length of a string is shown in Fig. 14.4.12. Using the scale on the given axis, find
(i) The amplitude of the wave
(ii) The wavelength of the wave
(iii) If the frequency of the wave is 10 Hz, What is the speed of the wave?
(iv) What is the initial phase of the wave ?
(v) What is the phase difference between two points separated by a distance 10 cm ?
(vi) If this wave is made to travel through water what is the wavelength of the wave, if the speed of, the waves in water is 10 m/s.
View SolutionA wave of frequency 500Hz has a wave velocity of 350m/s.
(a) Find the distance between two points which are 60∘ out of phase.
(b) Find the phase difference between two displacement at a certain point at time 10−3s apart.
View SolutionA wave of frequency 500Hz has a wave velocity of 350m/s.
(a) Find the distance between two points which are 60∘ out of phase.
(b) Find the phase difference between two displacement at a certain point at time 10−3s apart.
View SolutionA sound wave of frequency 100 Hz is travelling in air. The speed of sound in air is 350ms−1 (a) By how much is the phase changed at a given point in 2.5 ms ? (b) What is the phase difference at a given instant between two points separated by a distance of 10.0 cm along the direction of propagation ?
View Solution
