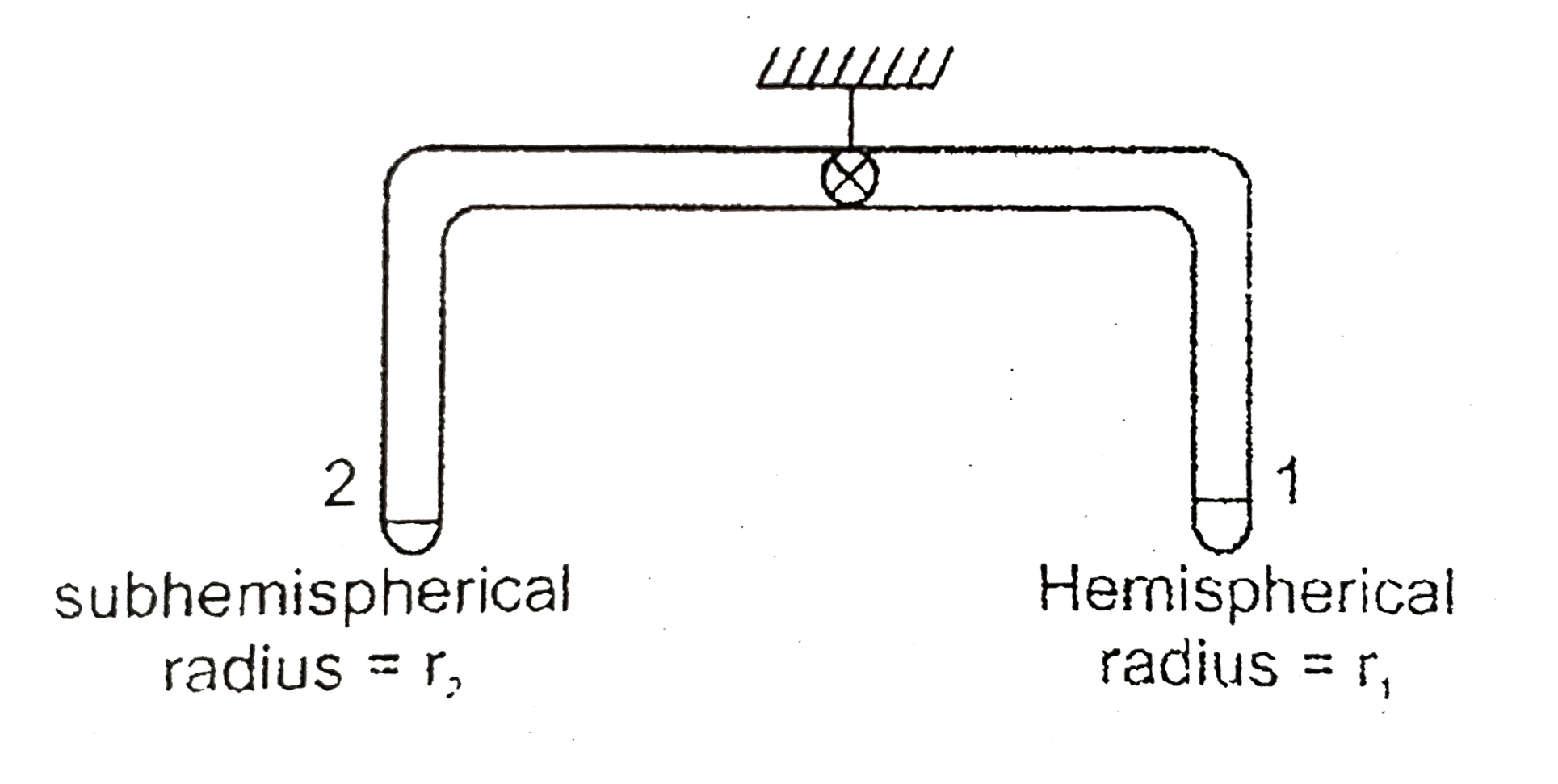
A glass tube of uniform internal radius (r) has a valve separating the two identical ends. Initially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble of radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve.

air from end 1 flows towards 2. No change in the volume of the soap bubbles
air from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreases
no change occurs
air form end 2 flows towards end 1. Volume of the soap bubble at end 1 increases.
The correct Answer is:B
Pressure inside tube =P=P0+4Tr
∴P2<P1 (since r2>r1)
Hence pressure on side 1 will be greater than side 2. So air from end 1 flows towards end 2.
Topper's Solved these Questions
- SURFACE TENSIONBook:RESONANCE ENGLISHChapter:SURFACE TENSIONExercise:Exercise- 3 PART - II
Explore 7 Videos
- SURFACE TENSIONBook:RESONANCE ENGLISHChapter:SURFACE TENSIONExercise:Advanced Level Problems
Explore 17 Videos
- SURFACE TENSIONBook:RESONANCE ENGLISHChapter:SURFACE TENSIONExercise:Exercise- 2 PART - IV
Explore 5 Videos
- STRING WAVESBook:RESONANCE ENGLISHChapter:STRING WAVESExercise:Exercise
Explore 32 Videos
- UNITS, DIMENSION & MEASUREMENTBook:RESONANCE ENGLISHChapter:UNITS, DIMENSION & MEASUREMENTExercise:Exercise
Explore 27 Videos
Similar Questions
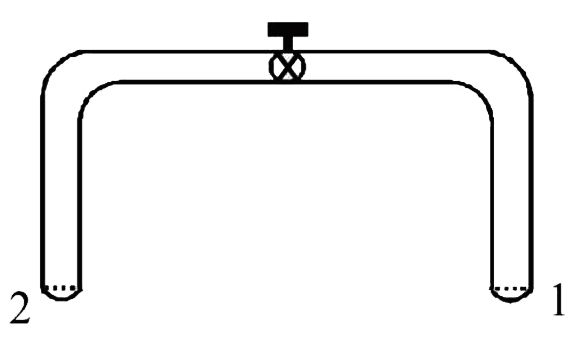
A glass tube of uniform internal radius(r) has a valve separating the two identical ends. Intially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble or radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve,
View SolutionTwo soap bubbles with radius 2r and 3r come in contact. Their common surface has a radius of curvature nr, then find the value of n
View Solution
Knowledge Check
Two spherical soap bubbles of radii r1andr2 in vaccum coalesce under isothermal conditions. The resulting bubble has a radius R such that
A(r1+r2)/2BR=[r1r2]/r1+r+(2)CR=√(r21+r22)DR=r1+r2
A semicircular metallic disc of radius R has two small cavities of radii r1and r2 as shown in the figure. On heating the disc

View SolutionAn isolated and charged spherical soap bubble has a radius 'r' and the pressure inside is atmospheric. If 'T' is the surface tension of soap solution, then charge on drop is:
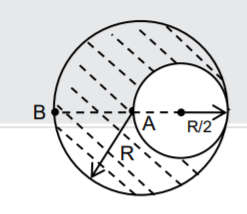
View SolutionA soap bubble A of radius 0.03 m and another bubble B of radius 0.04 m are brought together, so that the combined bubble has a common interface of radius r, then the value of r is
View SolutionA solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
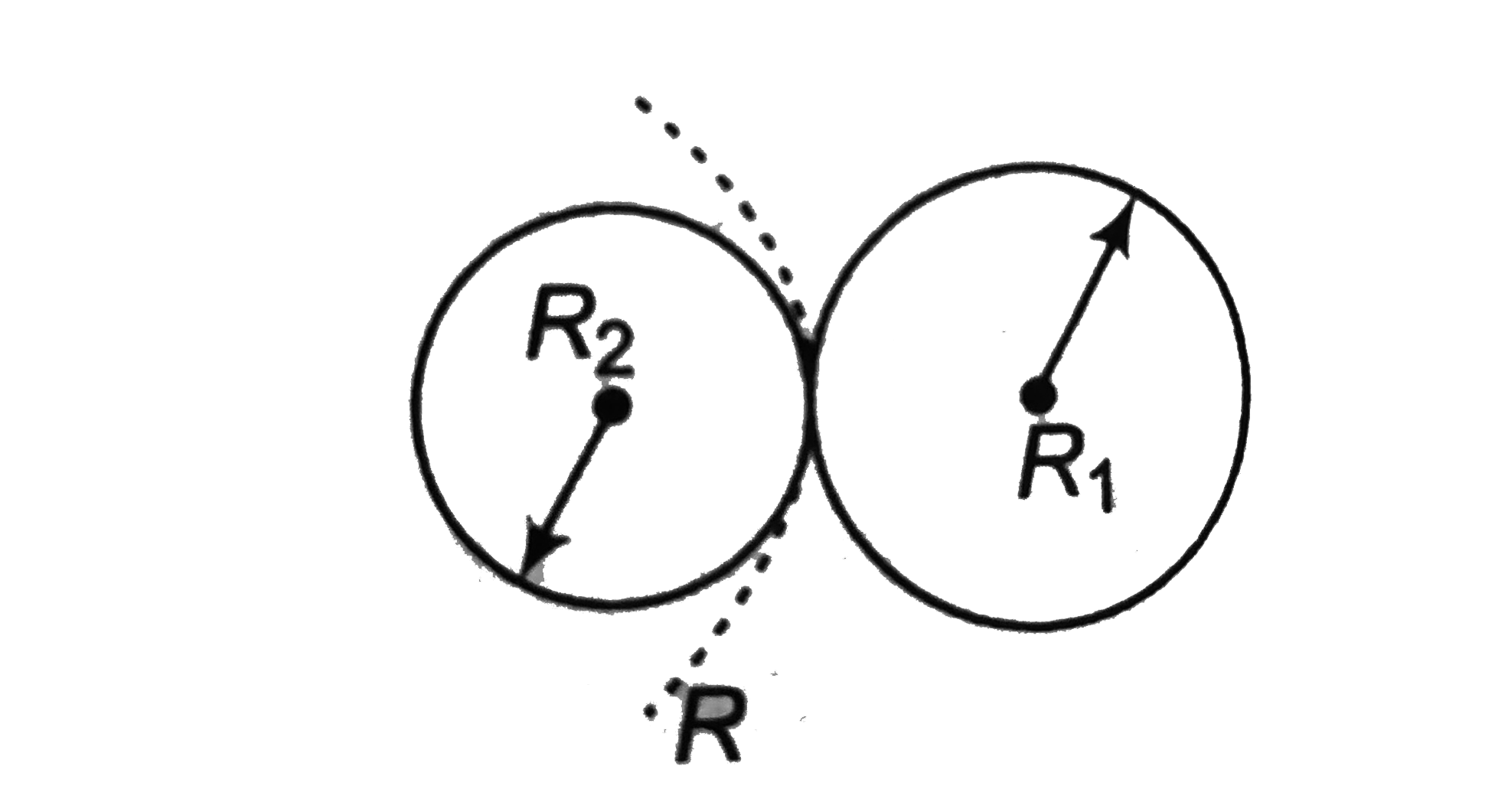
View SolutionTwo soap bubble of different radii R1 and R2(<R1) coalesce to form an interface of radius R as shown in figure. The correct value of R is
 .
.
View SolutionA small particle of mass m moving inside a heavy, hollow and straight tube along the tube axis undergoes elastic collision at two ends. The tube has no friction and it is closed at one end by a flat surface while the other end is fitted with a heavy movable flat piston as shown in figure. When the distance of the piston from closed end is L=L0 the particle speed is v=v0 The piston is moved inward at a very low speed V such that V<<dLLv0, where dL is the infinitesimal displacement of the piston. Which of the following statements(s) is(are) correct?
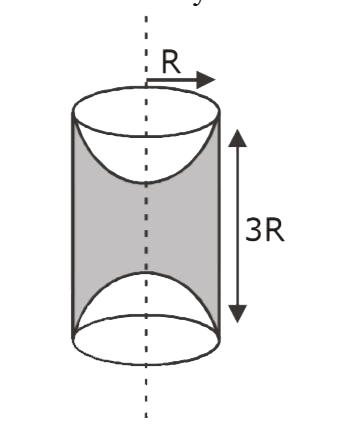
View SolutionA solid cylinder of radius R & length 3R is made of a metarial having density ρ . Now two hemispheres each of radius R is removed from two ends of cylinder as shown in figure. Determine the moment of inertia of this object about axis of cylinder?
View Solution