A glass tube of uniform internal radius(r) has a valve separating the two identical ends. Intially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble or radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve,

Air from end 1 flows towards end 2. There is no change in the volume of the soap bubble.
Air from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreases.
No change occurs.
Air from end 2 flows towards end 1. Volume of the soap bubble at end 1 increases.
The correct Answer is:B
△p1=4Tr1 and △p2=4Tr2
r1<r2∴△p1>△p2
Therefore air will flow from 1 to 2 and volume of bubble at end 1 will increase.
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - LC_TYPE
3 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Fill In The Blanks
1 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
A glass tube of uniform internal radius (r) has a valve separating the two identical ends. Initially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble of radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve.

View SolutionTwo soap bubbles with radius 2r and 3r come in contact. Their common surface has a radius of curvature nr, then find the value of n
View Solution
Knowledge Check
Two spherical soap bubbles of radii r1andr2 in vaccum coalesce under isothermal conditions. The resulting bubble has a radius R such that
A(r1+r2)/2BR=[r1r2]/r1+r+(2)CR=√(r21+r22)DR=r1+r2
A semicircular metallic disc of radius R has two small cavities of radii r1and r2 as shown in the figure. On heating the disc

View SolutionAn isolated and charged spherical soap bubble has a radius 'r' and the pressure inside is atmospheric. If 'T' is the surface tension of soap solution, then charge on drop is:
View SolutionA soap bubble A of radius 0.03 m and another bubble B of radius 0.04 m are brought together, so that the combined bubble has a common interface of radius r, then the value of r is
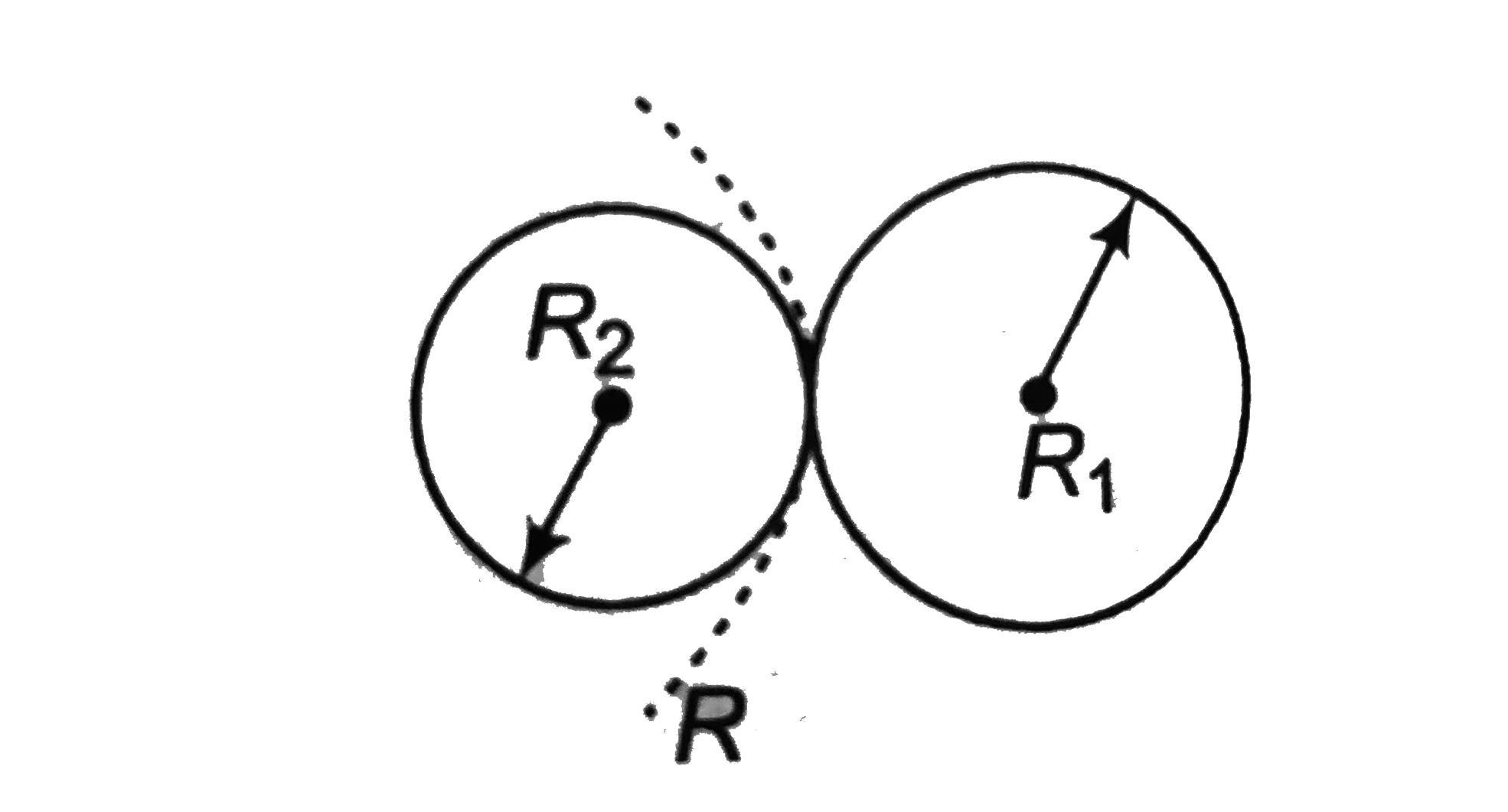
View SolutionTwo soap bubble of different radii R1 and R2(<R1) coalesce to form an interface of radius R as shown in figure. The correct value of R is
 .
.
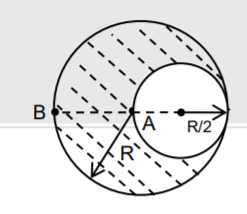
View SolutionA solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
View SolutionA small particle of mass m moving inside a heavy, hollow and straight tube along the tube axis undergoes elastic collision at two ends. The tube has no friction and it is closed at one end by a flat surface while the other end is fitted with a heavy movable flat piston as shown in figure. When the distance of the piston from closed end is L=L0 the particle speed is v=v0 The piston is moved inward at a very low speed V such that V<<dLLv0, where dL is the infinitesimal displacement of the piston. Which of the following statements(s) is(are) correct?
View SolutionA solid cylinder of radius R & length 3R is made of a metarial having density ρ . Now two hemispheres each of radius R is removed from two ends of cylinder as shown in figure. Determine the moment of inertia of this object about axis of cylinder?

View Solution
