Tension in a uniform string of length L varies with length uniformly. At one end A tension is T0 and at other end B it is 16T0. If mass per unit length of string is μ. Choose the correct options (s)
Time taken by a pulse to move from end A and B is 25L√μT0
Time taken by a pulse to move from end A to end B is 215√μLT0(√15−1)
Tension in the string as function of distance x from end A is T=T0+15T0Lx
Tension in the string as function of distance x from end A is T=T0+15T0Lx
The correct Answer is:A, C
To solve the problem, we need to analyze the tension in the uniform string and derive the relationship for tension as a function of distance along the string. We will also determine the time taken for a wave pulse to travel along the string.
1. Understanding the Problem:
- The tension at one end (A) of the string is T0 and at the other end (B) is 16T0.
- The length of the string is L and the mass per unit length is μ.
2. Finding the Tension as a Function of Distance:
- Since the tension varies uniformly from T0 to 16T0, we can express the tension T(x) at a distance x from end A as:
T(x)=T0+(16T0−T0L)x
- Simplifying this gives:
T(x)=T0+15T0Lx
- Therefore, the tension at any point x along the string is:
T(x)=T0+15T0Lx
3. Finding the Wave Velocity:
- The velocity v of a wave in a string is given by:
v=√Tμ
- Substituting T(x) into this equation gives:
v(x)=
⎷T0+15T0Lxμ
4. Time Taken for a Pulse to Travel:
- The time taken dt for a small distance dx can be expressed as:
dt=dxv(x)=dx√T0+15T0Lxμ
- Rearranging gives:
dt=dx√μ√T0+15T0Lx
- To find the total time T taken for the pulse to travel from x=0 to x=L, we integrate:
T=∫L0√μ√T0+15T0Lxdx
5. Evaluating the Integral:
- Let u=T0+15T0Lx, then du=15T0Ldx or dx=L15T0du.
- Changing the limits accordingly, when x=0, u=T0 and when x=L, u=16T0.
- The integral becomes:
T=∫16T0T0√μ√u⋅L15T0du
- Evaluating this integral gives:
T=L√μ15T0(2√u)16T0T0=L√μ15T0(2√16T0−2√T0)
- Simplifying this results in:
T=L√μ15T0⋅2(4−1)√T0=6L√μT015T0=2L√μ5√T0
Final Answers:
- The tension in the string as a function of distance x is:
T(x)=T0+15T0Lx
- The time taken for a pulse to travel from A to B is:
T=2L√μ5√T0
- The tension at one end (A) of the string is T0 and at the other end (B) is 16T0.
- The length of the string is L and the mass per unit length is μ.
- Since the tension varies uniformly from T0 to 16T0, we can express the tension T(x) at a distance x from end A as:
T(x)=T0+(16T0−T0L)x
- Simplifying this gives:
T(x)=T0+15T0Lx
- Therefore, the tension at any point x along the string is:
T(x)=T0+15T0Lx
- The velocity v of a wave in a string is given by:
v=√Tμ
- Substituting T(x) into this equation gives:
v(x)=
⎷T0+15T0Lxμ
- The time taken dt for a small distance dx can be expressed as:
dt=dxv(x)=dx√T0+15T0Lxμ
- Rearranging gives:
dt=dx√μ√T0+15T0Lx
- To find the total time T taken for the pulse to travel from x=0 to x=L, we integrate:
T=∫L0√μ√T0+15T0Lxdx
- Let u=T0+15T0Lx, then du=15T0Ldx or dx=L15T0du.
- Changing the limits accordingly, when x=0, u=T0 and when x=L, u=16T0.
- The integral becomes:
T=∫16T0T0√μ√u⋅L15T0du
- Evaluating this integral gives:
T=L√μ15T0(2√u)16T0T0=L√μ15T0(2√16T0−2√T0)
- Simplifying this results in:
T=L√μ15T0⋅2(4−1)√T0=6L√μT015T0=2L√μ5√T0
- The tension in the string as a function of distance x is:
T(x)=T0+15T0Lx
- The time taken for a pulse to travel from A to B is:
T=2L√μ5√T0
Similar Questions
The length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. Then natural length of the wire is
View SolutionA light string is tied at one end to a fixed support and to a heavy string of equal length L at the other end as shown in figure. A block of mass m is tied to the free end of heavy string. Mass per unit length of the strings are μ and 9μ and the tension is T. Find the possible values of frequencies such that junction of two wire point A is a node.

View SolutionThe length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. The natural length of the wire is
View SolutionThe length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. The natural length of the wire is
View SolutionA perfectly straight protion of a uniform rope has mass M and length L . At end A of the segment, the tension in the rope is TA and at end B it is TB(TB>TA) . Neglect effect of gravity and no contact force acts on the rope in between points A and B . The tension in the rope at a distance L/5 from end A is.
View SolutionA perfectly straight protion of a uniform rope has mass M and length L . At end A of the segment, the tension in the rope is TA and at end B it is TB(TB>TA) . Neglect effect of gravity and no contact force acts on the rope in between points A and B . The tension in the rope at a distance L/5 from end A is.
View Solution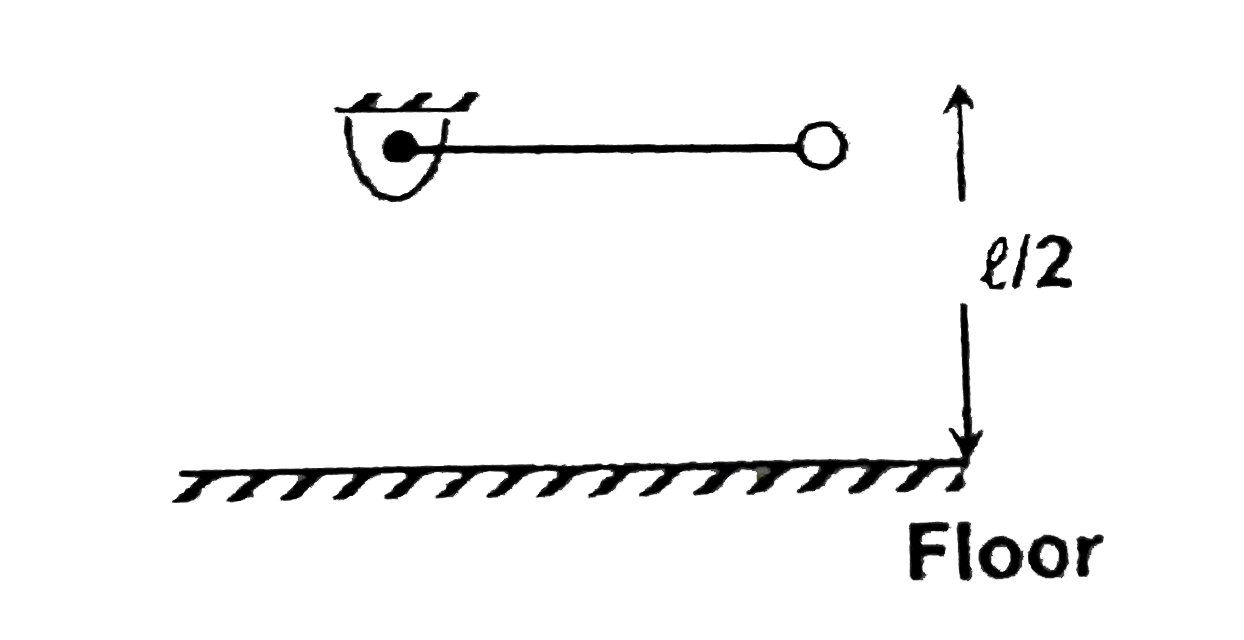
A bob of mass m connected to the end of an inextensible string of length l, is released from position shown in figure. If impacts of bob with smooth floors is perfectly inelastic. Choose the correct options (s)
View SolutionDerive an expression for the velocity of pulse in a in stretched in string under a tension T and μ is the mass per unit length of the sting.
View SolutionThe frequency (f) of a stretched string depends upen the tension F (dimensions of form ) of the string and the mass per unit length mu of string .Derive the formula for frequency
View SolutionOne end of a string of length L is tied to the ceiling of a lift acceleration upwards with an acceleration 2g. The other end of the string is free. The linear mass density of the string varies linearly from 0→λ from bottom to top. Choose the correct option(s)
View Solution
