One end of a string of length L is tied to the ceiling of a lift acceleration upwards with an acceleration 2g. The other end of the string is free. The linear mass density of the string varies linearly from 0→λ from bottom to top. Choose the correct option(s)
The velocity of the wave in the string will be 0.
The acceleration (relative to string) of the wave on the string will be 3g/4 every where.
The time taken by a pulse to reach from bottom to will be √8L/3g.
The time taken by a pulse to reach from bottom to top will be √4L/3g.
The correct Answer is:B, C
To solve the problem regarding the string tied to a ceiling in an accelerating lift, we need to analyze the forces acting on the string due to its variable mass density and the acceleration of the lift.
1. Understanding the System:
- The string has a length L and a linear mass density λ that varies from 0 at the bottom to λ at the top.
- The lift is accelerating upwards with an acceleration 2g, where g is the acceleration due to gravity.
2. Determine the Mass of the String:
- The mass density varies linearly, so we can express the mass density as:
μ(y)=λLy
where y is the distance from the bottom of the string.
- The total mass m of the string can be calculated by integrating the mass density along the length of the string:
m=∫L0μ(y)dy=∫L0λLydy=λL⋅L22=λL2
3. Calculate the Tension in the String:
- The tension T at a distance y from the bottom of the string can be expressed as:
T(y)=m(y)⋅(2g)=(λLy)⋅(2g)=2λgLy
- Here, m(y) is the mass of the string below point y.
4. Determine the Total Force:
- The total force acting on the string due to the lift's acceleration is:
F=T(y)−m(y)g=2λgLy−(λLy)g=(2λgLy−λgLy)=λgLy
- This indicates that the tension increases linearly with y.
5. Conclusion:
- The tension in the string varies linearly from 0 at the bottom to 2λgLL=2λg at the top.
- The correct options would depend on the specific choices given in the question, but we have established the behavior of the tension in the string under the given conditions.
- The string has a length L and a linear mass density λ that varies from 0 at the bottom to λ at the top.
- The lift is accelerating upwards with an acceleration 2g, where g is the acceleration due to gravity.
- The mass density varies linearly, so we can express the mass density as:
μ(y)=λLy
where y is the distance from the bottom of the string.
- The total mass m of the string can be calculated by integrating the mass density along the length of the string:
m=∫L0μ(y)dy=∫L0λLydy=λL⋅L22=λL2
- The tension T at a distance y from the bottom of the string can be expressed as:
T(y)=m(y)⋅(2g)=(λLy)⋅(2g)=2λgLy
- Here, m(y) is the mass of the string below point y.
- The total force acting on the string due to the lift's acceleration is:
F=T(y)−m(y)g=2λgLy−(λLy)g=(2λgLy−λgLy)=λgLy
- This indicates that the tension increases linearly with y.
- The tension in the string varies linearly from 0 at the bottom to 2λgLL=2λg at the top.
- The correct options would depend on the specific choices given in the question, but we have established the behavior of the tension in the string under the given conditions.
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
One end of a string of length L is tied to the celling of lift accelerating upwards with an accelerating 2g The other end of the string is free. The linear mass density of the string varies linearly from 0 of λ from bottom to top :-
View SolutionOne end of a string of length L is tied to the ceiling of a lift accelerating upwards with an acceleration 2g. The other end o the string is free. The linear mass density of the string varies linearly from 0 to λ from bottom to top. The acceleration of a wave pulled through out the string is pg4. Find p.
View SolutionA small metallic sphere of mass m is suspended from the ceiling of a car accelerating on a horizontal road with constant acceleration a. The tension in the string attached with metallic sphere is
View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View SolutionA body of mass M is hanging by an inextensible string of mass m. If the free end of the string accelerates up with constant acceleration a. find the variation of tension in the string a function of the distance measured from the mass M (bottom of the string).

View SolutionA standing wave is produced on a string on a string clamped at one end and free at the other. The length of the string
View SolutionThe acceleration of the 2 kg block if the free end of string is pulled with a force of 20 N as shown is
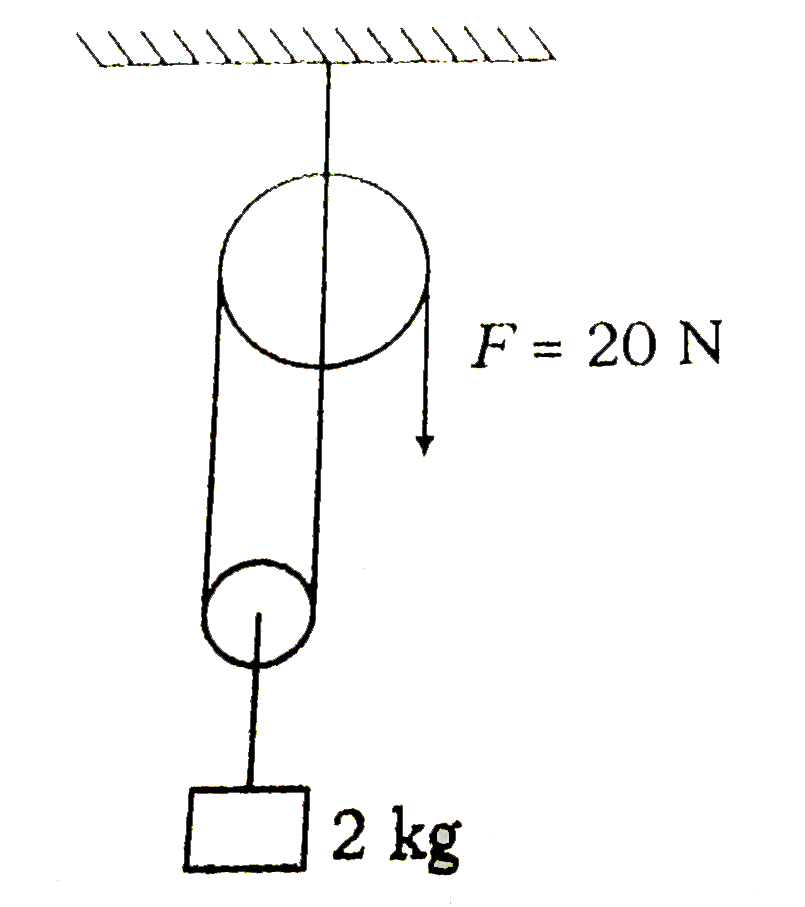
View SolutionA pendulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road. Find the angle made by the string with the vertical.
View SolutionA lift of mass 200 kg is moving upward with an acceleration of 3m/s2 . If g=10m/s2 then the tension of string of the lift will be :
View SolutionA uniform rod of mass m length l is attached to smooth hinge at end A and to a string at end B as shown in figure. It is at rest. The angular acceleration of the rod just after the string is cut is :

View Solution
