Define the following in photoelectric effect phenomenon
(a) (i) work function
(ii) Stopping potential (cut-off potential)
(b) calculate energy of photon of wavelenght 3.31Å
Step-by-Step Solution
1. Convert Wavelength to Meters:
3.31Å=3.31×10−10m
2. Use the Energy Formula:
The energy E of a photon can be calculated using the formula:
E=hcλ
where:
- h=6.626×10−34J s (Planck's constant)
- c=3×108m/s (speed of light)
- λ=3.31×10−10m (wavelength in meters)
3. Substitute the Values:
E=(6.626×10−34J s)(3×108m/s)3.31×10−10m
4. Calculate the Energy:
E=1.9878×10−25J m3.31×10−10m≈6.00×10−16J
Thus, the energy of the photon with a wavelength of 3.31Å is approximately 6.00×10−16J.
3.31Å=3.31×10−10m
The energy E of a photon can be calculated using the formula:
E=hcλ
where:
- h=6.626×10−34J s (Planck's constant)
- c=3×108m/s (speed of light)
- λ=3.31×10−10m (wavelength in meters)
E=(6.626×10−34J s)(3×108m/s)3.31×10−10m
E=1.9878×10−25J m3.31×10−10m≈6.00×10−16J
Topper's Solved these Questions
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems
17 Videos
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise-2 Part-III : Comprehension
12 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - HIGH LEVEL PROBLEMS
11 Videos
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - High Level Problems
16 Videos
Similar Questions
In photo-electric effect, what is meant by the terms:
(i) Work function of a metal.
(ii) Stopping potential.
View SolutionLight of energy 2.0 eV falls on a metal of work function 1.4 eV . The stopping potential is
View SolutionDefine the following terms :
(i) Kraft temperature
(ii) Peptization
(iii) Electrokinetic potential
View SolutionDefine the term 'stopping potential' in relation to photoelectric effect.
View SolutionLight of wavelength 488 nm is produced by an argon laser which is used in the photoelectric effect. When light from this spectral line is incident on the emitter, the stopping (cut - off) potential of photoelectrons is 0.38 V. Find the work function of the material from which the emitter is made.
View SolutionIn an experiment of photoelectric effect, the graph of maximum kinetic energy EK of the emitted photoelectrons versus the frequency v of the incident light is a straight line AB as shown in Figure below:
Find : (i) Threshold frequency of the metal.
(ii) work function of the metal
(iii) Stopping potential for the photoelectrons emitted by the light of frequency v=30×1014 Hz.
View SolutionIn photoelectric effect the work function of a metal is 3.5 eV. The emitted electrons can be stopped by applying a potential of –1.2 V. Then
View SolutionThe emission of electrons from a metal surface exposed rto light radaition of appropriate wavelength is called photoelectroic effect .The emmited electron are called photo=-weklectron work function of threshold energy may be defined as the minimum amount of energy required to ejercted electron from a most surface .According to Einstein
Maximum kinetic energy of ejected electron = Aborbed energy - Work function
12mv2max=h(v)−h(vn)=hv[1λ−01λn]
Where vn and λ0 are thereshold frequency and threshold wavelength respectively
Sopping potential : it is the miximum potential at which the photoelectric current becomes zero if V0 is the stopping potential eV0=h(v−v0)
The stopping potential as a function on electron frtequency is plotted for two photoelectric surface A abd B The graph show that the work function of A is
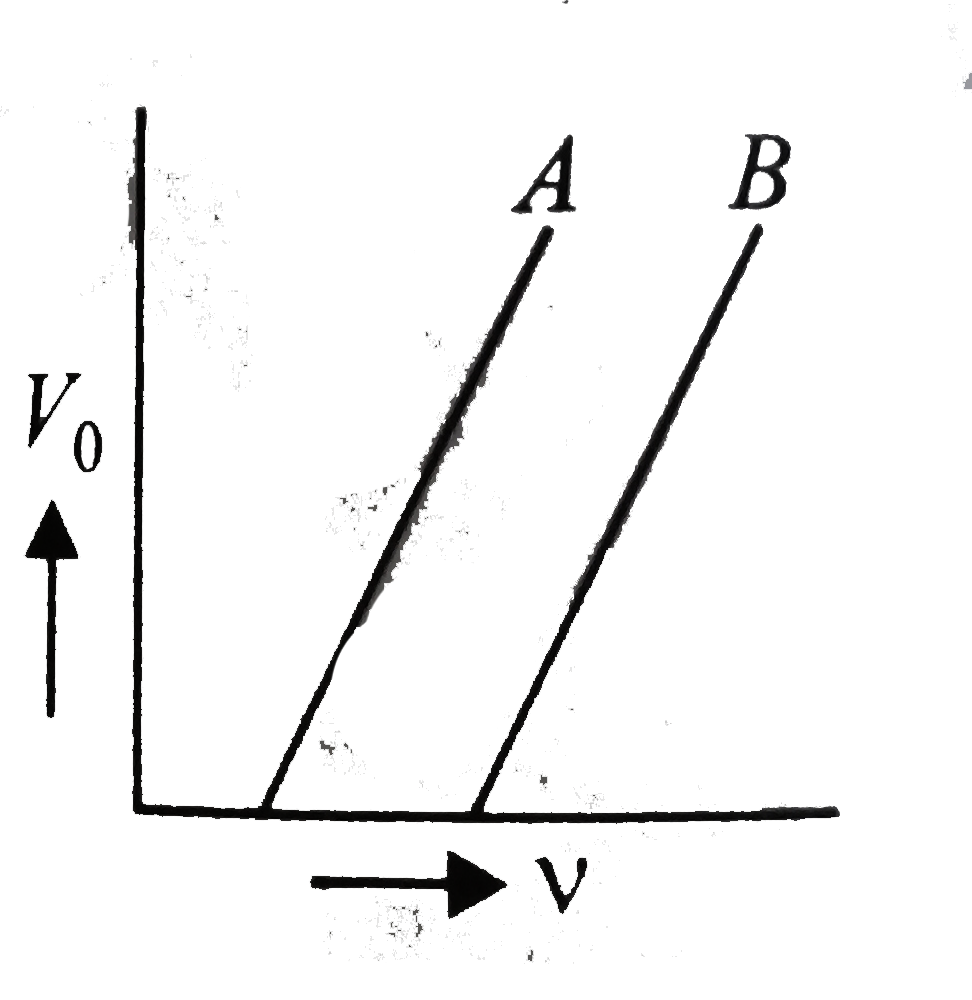
View SolutionIn an experiment on photo electric emission, following observations were made,
(i) Wavelength of the incident light =1.98×10−7m,
(ii) Stopping potential =2.5volt.
Find: (a) Kinetic energy of photoelectrons with maximum speed.
(b) Work function and
(c )Threshold frequency,
View SolutionThe electron in the hydrogen atom jumps from excited state (n=3) to its ground state (n=1) and the photons thus emitted irradiate a photosensitive material. If the work function of the material is 5.1eV, the stopping potential is estimated to be: (The energy of the electron in nth state is En=−13.6/n2eV)
View Solution
