In an experiment on photo electric emission, following observations were made,
(i) Wavelength of the incident light =1.98×10−7m,
(ii) Stopping potential =2.5volt.
Find: (a) Kinetic energy of photoelectrons with maximum speed.
(b) Work function and
(c )Threshold frequency,
To solve the problem step by step, we will follow the instructions given in the question.
Step 1: Calculate the Kinetic Energy of Photoelectrons
The kinetic energy (KE) of photoelectrons can be calculated using the stopping potential (V) with the formula:
KE=eV
Where:
- e is the charge of an electron, approximately 1.6×10−19 coulombs.
- V is the stopping potential, given as 2.5 volts.
Substituting the values:
KE=1.6×10−19C×2.5V=4.0×10−19J
To convert this energy into electron volts (eV), we can directly use the stopping potential:
KE=2.5eV
Step 2: Calculate the Work Function (φ)
The work function (φ) can be calculated using the energy of the incident photons (E) and the kinetic energy of the emitted photoelectrons:
E=ϕ+KE
The energy of the incident photons can be calculated using the formula:
E=hcλ
Where:
- h is Planck's constant, approximately 6.63×10−34Js.
- c is the speed of light, approximately 3.0×108m/s.
- λ is the wavelength of the incident light, given as 1.98×10−7m.
Calculating E:
E=(6.63×10−34Js)(3.0×108m/s)1.98×10−7m=1.989×10−251.98×10−7≈1.006×10−18J
To convert this energy into electron volts:
E≈1.006×10−181.6×10−19≈6.29eV
Now substituting into the work function equation:
ϕ=E−KE=6.29eV−2.5eV=3.79eV
Step 3: Calculate the Threshold Frequency (ν₀)
The threshold frequency can be calculated using the work function:
ϕ=hν0
Rearranging gives:
ν0=ϕh
Substituting the values:
ν0=3.79eV×1.6×10−19J/eV6.63×10−34Js≈6.064×10−196.63×10−34≈9.15×1014Hz
Final Answers:
(a) Kinetic Energy of photoelectrons = 2.5 eV
(b) Work Function (φ) = 3.79 eV
(c) Threshold Frequency (ν₀) = 9.15 x 10¹⁴ Hz
---
- e is the charge of an electron, approximately 1.6×10−19 coulombs.
- V is the stopping potential, given as 2.5 volts.
- h is Planck's constant, approximately 6.63×10−34Js.
- c is the speed of light, approximately 3.0×108m/s.
- λ is the wavelength of the incident light, given as 1.98×10−7m.
(a) Kinetic Energy of photoelectrons = 2.5 eV
(b) Work Function (φ) = 3.79 eV
(c) Threshold Frequency (ν₀) = 9.15 x 10¹⁴ Hz
Topper's Solved these Questions
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Solved miscellaneous problems
14 Videos
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise 1 Part-1 subjective questions
35 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - HIGH LEVEL PROBLEMS
11 Videos
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - High Level Problems
16 Videos
Similar Questions
In an experiment on photoelectric emission from a metallic surface ,wavelength of incident light 2×10−7 m and stopping potential is 2.5V .The threshold frequency of the metal (in Hz) approximately
(Charge of electrons e=1.6×10−19C, Planck's constant ,h=6.6×10−34J−s)
View SolutionCalculate the velocity of a photo-electron if the work function of the target material is 1.24eV and the wavelength of incident light is 4.36×10−7m. What retarding potential is necessary to stop the emission of the electrons?
View SolutionCalculate the valocity of a photoelectron if the work function of the target material is 1.24eV and the wavelength of incident light is 4.36×10−7m. What retarding potentia is necessary to stop the emission of the electrons?
View SolutionPhotoelectric emission is observed from a metallic surface for frequencies v1 and v2 of the incident light rays (v1>v2). If the maximum values of kinetic energy of the photoelectrons emitted in the two cases are in the ratio of 1:k , then the threshold frequency of the metallic surface is
View SolutionPhotoelectric emission is observed from a metallic surface for frequencies v1 and v2 of the incident light rays (v1>v2). If the maximum values of kinetic energy of the photoelectrons emitted in the two cases are in the ratio of 1:k , then the threshold frequency of the metallic surface is
View SolutionPhotoelectric emission is observed from a surface for frequencies v1andv2 of the incident radiation (v1>v2) . If maximum kinetic energies of the photo electrons in the two cases are in the ratio 1:K , then the threshold frequency is given by:
View SolutionThe stopping potential for photoelectrons emitted from a surface illuminated by light wavelength of 5893A is 0.36V. Calculate the maximum kinetic energy of photoelectrons, the work function of the surface, and the threshold frequency.
View SolutionPhotoelectric emission is observed from a surface for frequencies v1andv2 of incident radiations
(v1>v2). If the maximum kinetic energy of photoelectrons in the two cases are in the ratio of 2:1 then threshold frequency v0 is given by.
View SolutionIn an experiment of photo-electric effect, the graph of maximum kinetic energy Ek of the emitted photoelectrons versus the frequency v of the incident light is a straight line AB as shown in figure below :
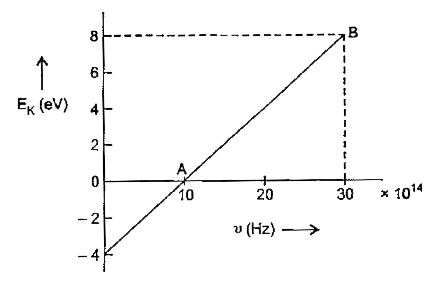
Stopping potential for the photoelectrons emitted by the light of frequency
v=30×1014Hz
View SolutionLight of wavelength 2000Å is incident on a metal surface of work function 3.0 eV. Find the minimum and maximum kinetic energy of the photoelectrons.
View Solution
