Draw a schematic diagram of the experiment used by. Davisson and Germer to establish the wave nature of electrons. Explain briefly how the de-Broglie wave relation experimentally verfied in case of electrons.
Step-by-Step Solution
Step 1: Schematic Diagram of the Davisson-Germer Experiment
1. Electron Gun: Draw an electron gun that emits electrons. This consists of a tungsten filament that is heated to release electrons when a high voltage (around 54 eV) is applied.
2. Nickel Target: Place a nickel plate opposite the electron gun. This plate will serve as the target for the electrons.
3. Detector: Position a detector at a certain angle (θ) from the normal to the nickel plate to measure the intensity of the reflected electrons.
4. Incident and Reflected Beams: Indicate the incident beam (IB) of electrons striking the nickel plate and the reflected beam (RB) coming off the plate at an angle θ.
Diagram:
E≤ctronGun||⊢−→IB(IncntBeam)||−−−−−−−−−−−−−−−−−|NickelPlate|−−−−−−−−−−−−−−−−−|⊢−→RB(Ref≤ctedBeam)|Detec→r
Step 2: Explanation of the Experiment
1. Electron Emission: When the tungsten filament is heated, electrons are emitted due to thermionic emission.
2. Electron Acceleration: These electrons are accelerated towards the nickel target by the applied voltage (54 eV).
3. Electron Interaction: Upon striking the nickel plate, the electrons interact with the electrons in the nickel, leading to scattering.
4. Detection of Intensity: The detector measures the intensity of the reflected electrons at various angles. Instead of a random scattering pattern, specific angles show maxima in intensity.
5. Interference Pattern: The observed maxima and minima in intensity indicate an interference pattern, suggesting that electrons exhibit wave-like behavior.
Step 3: Verification of de Broglie Wavelength
1. de Broglie Hypothesis: According to de Broglie, the wavelength (λ) of a particle is given by the relation λ = h / p, where p is the momentum (p = mv).
2. Kinetic Energy Relation: The kinetic energy (KE) of the electrons can be expressed as KE = eV, where e is the charge of the electron and V is the accelerating voltage.
3. Momentum Calculation: From kinetic energy, we can derive the momentum:
\(
p = \sqrt{2m \cdot KE} = \sqrt{2m \cdot eV}
\)
4. Substituting into de Broglie Equation: Substitute the expression for momentum into the de Broglie wavelength equation:
\(
λ = \frac{h}{\sqrt{2m \cdot eV}}
\)
5. Calculating Wavelength: For V = 54 eV, using known values for h (Planck's constant) and m (mass of the electron), we calculate λ.
6. Bragg's Law Verification: Using Bragg's law, λ can also be calculated from the crystal structure of nickel, and the results should match the de Broglie wavelength.
1. Electron Gun: Draw an electron gun that emits electrons. This consists of a tungsten filament that is heated to release electrons when a high voltage (around 54 eV) is applied.
2. Nickel Target: Place a nickel plate opposite the electron gun. This plate will serve as the target for the electrons.
3. Detector: Position a detector at a certain angle (θ) from the normal to the nickel plate to measure the intensity of the reflected electrons.
4. Incident and Reflected Beams: Indicate the incident beam (IB) of electrons striking the nickel plate and the reflected beam (RB) coming off the plate at an angle θ.
E≤ctronGun||⊢−→IB(IncntBeam)||−−−−−−−−−−−−−−−−−|NickelPlate|−−−−−−−−−−−−−−−−−|⊢−→RB(Ref≤ctedBeam)|Detec→r
1. Electron Emission: When the tungsten filament is heated, electrons are emitted due to thermionic emission.
2. Electron Acceleration: These electrons are accelerated towards the nickel target by the applied voltage (54 eV).
3. Electron Interaction: Upon striking the nickel plate, the electrons interact with the electrons in the nickel, leading to scattering.
4. Detection of Intensity: The detector measures the intensity of the reflected electrons at various angles. Instead of a random scattering pattern, specific angles show maxima in intensity.
5. Interference Pattern: The observed maxima and minima in intensity indicate an interference pattern, suggesting that electrons exhibit wave-like behavior.
1. de Broglie Hypothesis: According to de Broglie, the wavelength (λ) of a particle is given by the relation λ = h / p, where p is the momentum (p = mv).
2. Kinetic Energy Relation: The kinetic energy (KE) of the electrons can be expressed as KE = eV, where e is the charge of the electron and V is the accelerating voltage.
3. Momentum Calculation: From kinetic energy, we can derive the momentum:
\(
p = \sqrt{2m \cdot KE} = \sqrt{2m \cdot eV}
\)
4. Substituting into de Broglie Equation: Substitute the expression for momentum into the de Broglie wavelength equation:
\(
λ = \frac{h}{\sqrt{2m \cdot eV}}
\)
5. Calculating Wavelength: For V = 54 eV, using known values for h (Planck's constant) and m (mass of the electron), we calculate λ.
6. Bragg's Law Verification: Using Bragg's law, λ can also be calculated from the crystal structure of nickel, and the results should match the de Broglie wavelength.
Topper's Solved these Questions
- ATOMIC PHYSICSBook:RESONANCE ENGLISHChapter:ATOMIC PHYSICSExercise:Advanved level problems
Explore 17 Videos
- ATOMIC PHYSICSBook:RESONANCE ENGLISHChapter:ATOMIC PHYSICSExercise:Exercise-2 Part-III : Comprehension
Explore 12 Videos
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:HIGH LEVEL PROBLEMS
Explore 11 Videos
- CAPACITANCEBook:RESONANCE ENGLISHChapter:CAPACITANCEExercise:High Level Problems
Explore 16 Videos
Similar Questions
Knowledge Check
Assertion : The wave nature of electrons was first experimentally verified by Davisson and Germer Experiment.
Reason : From the electron diffraction measurements, the wavelength of metter waves was found to 0.165 nm.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
In experiment of Davisson-Germer, emitted electron from filament is accelerated through voltage V then de-Broglie wavelength of that electron will be _______m.
View SolutionThe De-Broglie wave length of electron in second exited state of hydrogen atom is
View SolutionDraw a labelled circuit diagram of n - p - n germanium transistor in common emitter configuration. Explain briefly, how this transistor is used as a voltage amplifier.
View SolutionDraw a schematic arrangement of the Geiger Marsden experiment. How did the scattering of α particles by a thin foil of gold provide an important way to determine an upper limit on the size of nucleus? Explain briefly.
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructiely
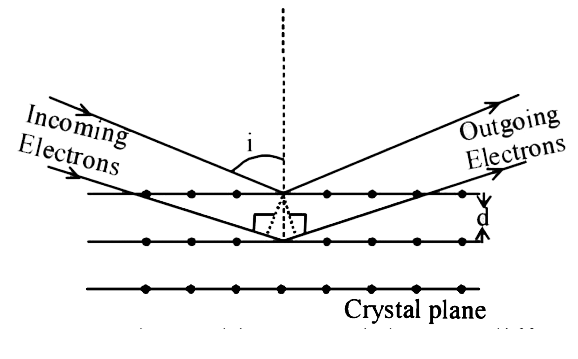
Electron accelerated by potential V are diffracted from a crystal if d=1Åandi=30∘,V should be about (h=6.6×10−34Js,me=9.1×10−31kg,e=1.6×10−19C)
View SolutionDual nature of matter was proposed by de Broglie in 1923, it was experimentally verified by Davisson and Germer by diffraction experiment. Wave haracter of matter has significance only for microscopic particles. De Broglie wavelength (λ) can be calculated using the relation, (λ)=hmv
where 'm' and 'v' are the mass and velocity of the particle.
Which among the following is not used to calculate the de Broglie wavelength ?
View SolutionThe wave character of moving electron was experimentally verified by :
(a)de-Broglie
(b)A-Einstein
(c)Garmer
(d)Schrodinger
View Solution

