For the D−T fusion reaction, find the rate at which deuterium & trithium are consumed to produce 1MW. The Q-value of D−T reactions is 17.6MeV & assume all the energy from the fusion rection is available.
The correct Answer is:2NA×117.6e×10−3Kg/s=1.179×10−9kg/s
3NA×117.6e×10−3kg/s=1.769×10−9kg/s
To solve the problem of finding the rate at which deuterium and tritium are consumed to produce 1 MW from the D-T fusion reaction, we can follow these steps:
Step 1: Understand the Energy Requirement
We need to produce 1 MW of power.
1 MW = 106 watts.
Step 2: Convert the Q-value to Joules
The Q-value for the D-T fusion reaction is given as 17.6 MeV. We need to convert this energy into joules for our calculations.
1 MeV = 1.6×10−13 joules.
So,
Q=17.6MeV=17.6×1.6×10−13J
Calculating this gives:
Q=28.16×10−13J
Step 3: Calculate the Number of Reactions per Second
To find the number of fusion reactions needed per second to produce 1 MW, we use the formula:
Number of reactions per second=PowerEnergy per reaction
Substituting the values we have:
Number of reactions per second=106W28.16×10−13J
Calculating this gives:
Number of reactions per second=10628.16×10−13≈3.55×1016reactions/second
Step 4: Determine the Rate of Consumption of Deuterium and Tritium
In the D-T fusion reaction, one deuterium nucleus and one tritium nucleus are consumed per reaction. Therefore, the rate at which deuterium and tritium are consumed is equal to the number of reactions per second.
Thus, the rate of consumption of deuterium and tritium is:
Rate of consumption of D and T=3.55×1016nuclei/second
Final Answer
The rate at which deuterium and tritium are consumed to produce 1 MW of power is approximately 3.55×1016 nuclei per second for each of D and T.
---
We need to produce 1 MW of power.
1 MW = 106 watts.
The Q-value for the D-T fusion reaction is given as 17.6 MeV. We need to convert this energy into joules for our calculations.
1 MeV = 1.6×10−13 joules.
Q=17.6MeV=17.6×1.6×10−13J
Calculating this gives:
Q=28.16×10−13J
To find the number of fusion reactions needed per second to produce 1 MW, we use the formula:
Number of reactions per second=PowerEnergy per reaction
Substituting the values we have:
Number of reactions per second=106W28.16×10−13J
Number of reactions per second=10628.16×10−13≈3.55×1016reactions/second
In the D-T fusion reaction, one deuterium nucleus and one tritium nucleus are consumed per reaction. Therefore, the rate at which deuterium and tritium are consumed is equal to the number of reactions per second.
Rate of consumption of D and T=3.55×1016nuclei/second
The rate at which deuterium and tritium are consumed to produce 1 MW of power is approximately 3.55×1016 nuclei per second for each of D and T.
Topper's Solved these Questions
- NUCLEAR PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Exercise-1 Part-2 Only one option correct type
27 Videos
- NUCLEAR PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Exercise 2 Part-1 Only one option correct type
20 Videos
- NUCLEAR PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Advanced level solutions
16 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
- REVISION DPPBOOK - RESONANCE ENGLISHCHAPTER - REVISION DPPEXERCISE - All Questions
463 Videos
Similar Questions
A fusion reaction of the type given below
.21D+.21D→.31T+.11p+ΔE
is most promising for the production of power. Here D and T stand for deuterium and tritium, respectively. Calculate the mass of deuterium required per day for a power output of 109W. Assume the efficiency of the process to be 50%.
Given : m(.21D)=2.01458amu, m(.31T)=3.01605amu
m(.11p)=1.00728amu and 1amu=930MeV.
View SolutionWhen a biochemical reaction is carried out in laboratory from outside of human body in the absence of enzyme, the rate of reaction obtained is 10−6 times, then activation energy of the reaction in the presence of enzyme is
(a)6RT
(b)P is required
(c)Different forms Ea obtained in laboratory
(d)cannot say any things
View Solution
Knowledge Check
A ancleus of mass number 220, initially at rest, emits an α-particle, If the Q-value of the reaction is 5.5 Me V, then the energy of the emitted α-particle will be
A4.4 MeVB5.4 MeVC5.6 MeVD6.5 MeV
For a reaction , 2A+D→3C, the rate of appearance of C at time t is 1.2×10−4mol L−1s−1 . Find the rate of reaction.
View SolutionIn the fusion reaction .21H+21H→32He+10n, the masses of deuteron, helium and neutron expressed in amu are 2.015,3.017and1.009 respectively. If 1kg of deuterium undergoes complete fusion, find the amount of total energy released. 1 amu =931.5MeV/c2.
View SolutionIn the fusion reaction _12H+21H→32He+10n, the masses of deuteron, helium and neutron expressed in amu are 2.015, 3.017 and 1.009 respectively. If 1 kg of deuterium undergoes complete fusion, find the amount of total energy released. 1 amu =931.5MeV/c2.
View SolutionConsider the following plots of rate constant versus 1T for four different reactions. Which of the following orders is correct for the activation energies of these reactions ?

View SolutionBoth the Cβ−HandCα−X bonds are breaking in the transition state of E2 reactions.The rate of E2 reactions is of second order.The rate shows primary isotopic (dueterium) effect. i.e. if Cβ−H is replaced by Cβ−D , the rate of reaction decreases sharply. The rate is also corelated with nucleofugality i.e. the ability of leaving group to leave.With a better nucleofuge, the rate of reaction increases.This is called he element effect.
The element effect is also observed in E1cB reactions in which the second step is rate determining and elimination of first order w.r.t conjugate base is observed.For E1cB reaction KH/KD=1, therefore proton abstraction is not involved in the rate determing step In D2O the incorporation of Deuterium at Cβ-H in the In E1 reaction only nucleofuge departs in slow step and a carbocation intermediate is formed.
For the given compounds I and II the rate of elimination by EtOΘ/EtOH shows KH/KD=7.1 What is the about this reaction

View SolutionThe radiations emitted by the sun are analyzed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
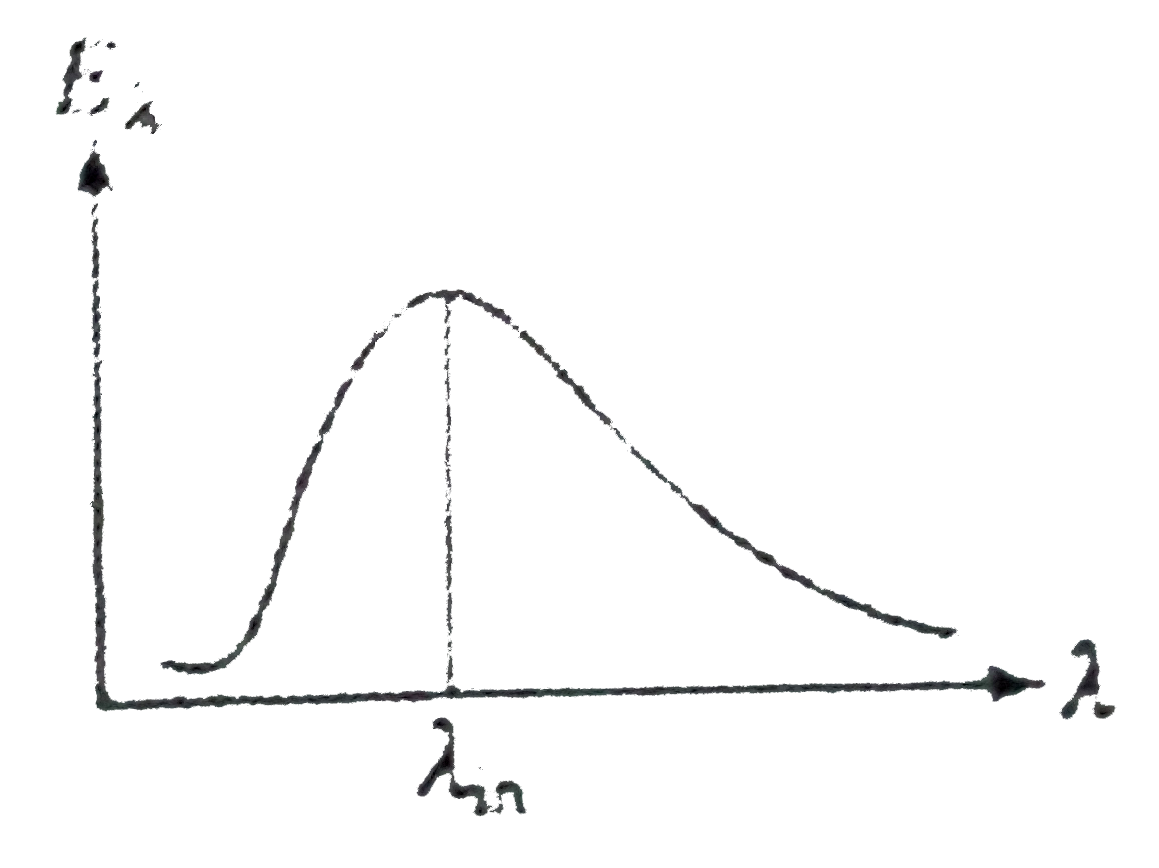
Assume the sun produces energy only by nuclear fusion of hydrogen nuclei and the fraction of nuclear mass of hydrogen that can be converted to energy is η. How long will the sun keep on emittied the energy if the mass of hydrogen at present in Sun's core is m?
View SolutionFor a first order reaction A(g)→2B(g)+C(g) at constant volume and 300 K, the total pressure at the beginning (t=0) and at time t ae P0andPt respectively. Initially, only A is present with concentration [A]0andt1/3 is the time required for the partial pressure of A to reach 1/3rd of its initial value. The correct options (s) is (are) :
(Assume that all these behave as ideal gases)
View Solution
