In the decay .64Cu→.64Ni+e−+v1 the maximum kinetic energy carried by the positron is found to be 0.680MeV (a) Find the energy of the neutrino which was emitted together with a positron of energy 0.180MeV (b) what is the momentum of this neutrion in kg−m/s ? Use the formula applicable to photon.
The correct Answer is:(a) (0.680−0.180)MeV=500keV
(b) 500×103ec=2.67×10−22kg−m/s
(a) KEofυ+KEofe+=Maximum energy ofe+
⇒KEofυ=(0.680−0.180)MeV=500KeV.
(b) p=EC=500×103×1.6×10−193×108Kg−m/s=2.67×10−22Kg−m/s.
Topper's Solved these Questions
- NUCLEAR PHYSICSBook:RESONANCE ENGLISHChapter:NUCLEAR PHYSICSExercise:Exercise-1 Part-2 Only one option correct type
Explore 27 Videos
- NUCLEAR PHYSICSBook:RESONANCE ENGLISHChapter:NUCLEAR PHYSICSExercise:Exercise 2 Part-1 Only one option correct type
Explore 20 Videos
- NUCLEAR PHYSICSBook:RESONANCE ENGLISHChapter:NUCLEAR PHYSICSExercise:Advanced level solutions
Explore 16 Videos
- GRAVITATIONBook:RESONANCE ENGLISHChapter:GRAVITATIONExercise:HIGH LEVEL PROBLEMS
Explore 16 Videos
- REVISION DPPBook:RESONANCE ENGLISHChapter:REVISION DPPExercise:All Questions
Explore 463 Videos
Similar Questions
In the decay Cu64→Ni64+e++v,
the maximum kinetic energy carried by the netrino which was emitted together with a positron of kinetic energy 0.150 meV? (a) what is the energy of the neutrino which was emitted togather with a positron of kinetic energy 0.150 MeV ? .(b)What is the momentum of this neutrino in kg m s−1?Use the formula applicable to photon.
View SolutionThe β−decay process , discovered around 1900 , is basically the decay of a neutron n. In the laboratory , a proton p and an electron e¯ are observed as the decay product of neutron. Therefore considering the decay of neutron as a two- body decay process, it was predicted theoretically that the kinetic energy of the electron should be a constant . But experimentally , it was observed that the electron kinetic energy has continuous spectrum Considering a three- body decay process , i.e.
n→p+e¯+¯νe, around 1930 , Pauli explained the observed electron energy spectrum. Assuming the anti-neutrino (¯νe) to be massaless and possessing negligible energy , and the neutrino to be at rest , momentum and energy conservation principle are applied. From this calculation , the maximum kinetic energy of the electron is 0.8×106eV The kinetic energy carried by the proton is only the recoil energy.
If the - neutrono had a mass of 3eV/c2 (where c is the speed of light ) insend of zero mass , what should be the range of the kinectic energy K. of the electron ?
View SolutionThe β-decay process, discovered around 1900, is basically the decay of a neutron (n), In the laboratory, a proton (p) and an electron (e−) are observed as the decay products of the neutron. Therefore, considering the decay of a neutron as a tro-body dcay process, it was observed that the electron kinetic energy has a continuous spectrum. Considering a three-body decay process i.e., n→p+e−+−ve, around 1930, Pauli explained the observed electron energy spectrum. Assuming the anti-neutrino (−Ve) to be massless and possessing negligible energy, and neutron to be at rest, momentum and energy conservation principles are applied. From this calculation, the maximum kinetic energy of the electron is 0.8×106eV. The kinetic energy carried by the proton is only the recoil energy.
If the anti-neutrino has a mass of 3eV/c2 (where c is the speed of light) instead of zero mass, what should be the range of the kinetic energy, K of the electron?
View SolutionA moving positron and electron both with kinetic energy 1 Me V annihilate with each other and emits two gamma photons. If the rest mass energy of an electron is 0.51 MeV, the wavelength of each photon is ?
View SolutionA nuclear raction is given us
P+15N→AZX+n
(a). Find, A,Z and identity the nucleus X. (b) Find the Q value of the reaction . ( c) If the proton were to collide with the .15N at rest, find the minimum KE needed by the proton to initiate the above reaction. (d) If the proton has twice energy in (c) and the outgoing neutron emerges at an angle of 90∘ with the direction of the incident proton, find the momentum of the protons and neutrons. [Given,m(p)=1.007825u,m(.15C)=15.0106u,m(.16N)=16.0061u,m(.15N)=15.000u),m(.16O)=15.9949u,m(u)=1.0086665u,m(.15O)=15.0031u,and1u≈931.5MeV.].
View SolutionGold .19879Au undergoes β− decay to an excited state of .19880Hg. If the excited state decays by emission of a γ-photon with energy 0.412MeV, the maximum kinetic energy of the electron emitted in the decay is (This maximum occurs when the antineutrino has negligble energy. The recoil enregy of the .19880Hg nucleus can be ignored. The masses of the neutral atoms in their ground states are 197.968255u for .19879Hg).
View SolutionLight form a dicharge tube containing hydrogen atoms falls on the surface of a piece of sodium. The kinetic energy of the fastest photoelectrons emitted from sodium is 0.73 eV. The work function for sodium is 1.82 eV. Find (a) the energy of the photons causing the photoelectrons emission.
(b) the quatum numbers of the two levels involved in the emission of these photons.
(c ) the change in the angular momentum of the electron in the hydrogen atom, in the above transition, and
(d) the recoil speed of the emitting atom assuming it to be at rest before the transition. (lonization potential of hydrogen is 13.6 eV.)
View SolutionThe conducting rod ab shown in figure makes contact with metal rails ca and db. The apparatus is in a uniform magnetic field 0.800T, perpendicular to the plane of the figure.
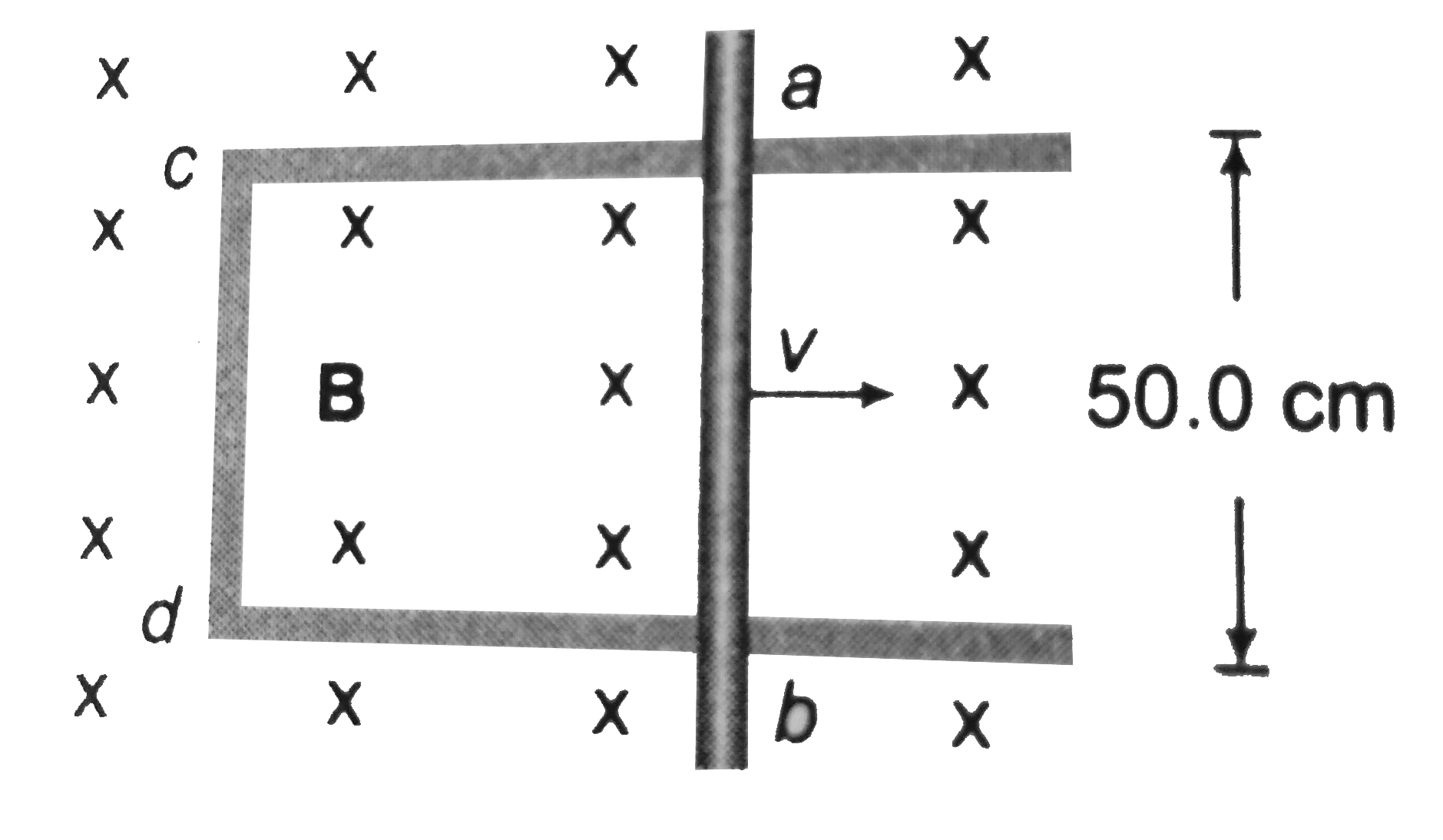
(a) Find the magnitude of the emf induced in the rod when it is moving toward the right with a speed 7.50m/s.
(b) In what direction does the current flow in the rod?
(c) If the resistance of the circuit abdc is 1.50Ω (assumed to be constant), find the force (magnitude and direction) required to keep the rod moving to the right with a constant speed of 7.50m/s. You can ignore friction.
(d) Compare the rate at which mechanical work is done by the force (Fu) with the rate at which thermal energy is developed in the circuit (I2R).
View Solution.^(239)Pu.94 is undergoing α−decay according to the equation .23994Pu→(.23597U)+.42He . The energy released in the process is mostly kinetic energy of the α-particle. However, a part of the energy is released as γ rays. What is the speed of the emiited α-particle if the γ rays radiated out have energy of 0.90MeV? Given: Mass of .23994Pu=239.05122u, mass of (.23597U)=235.04299u and mass of .41He=4.002602u(1u=931MeV).
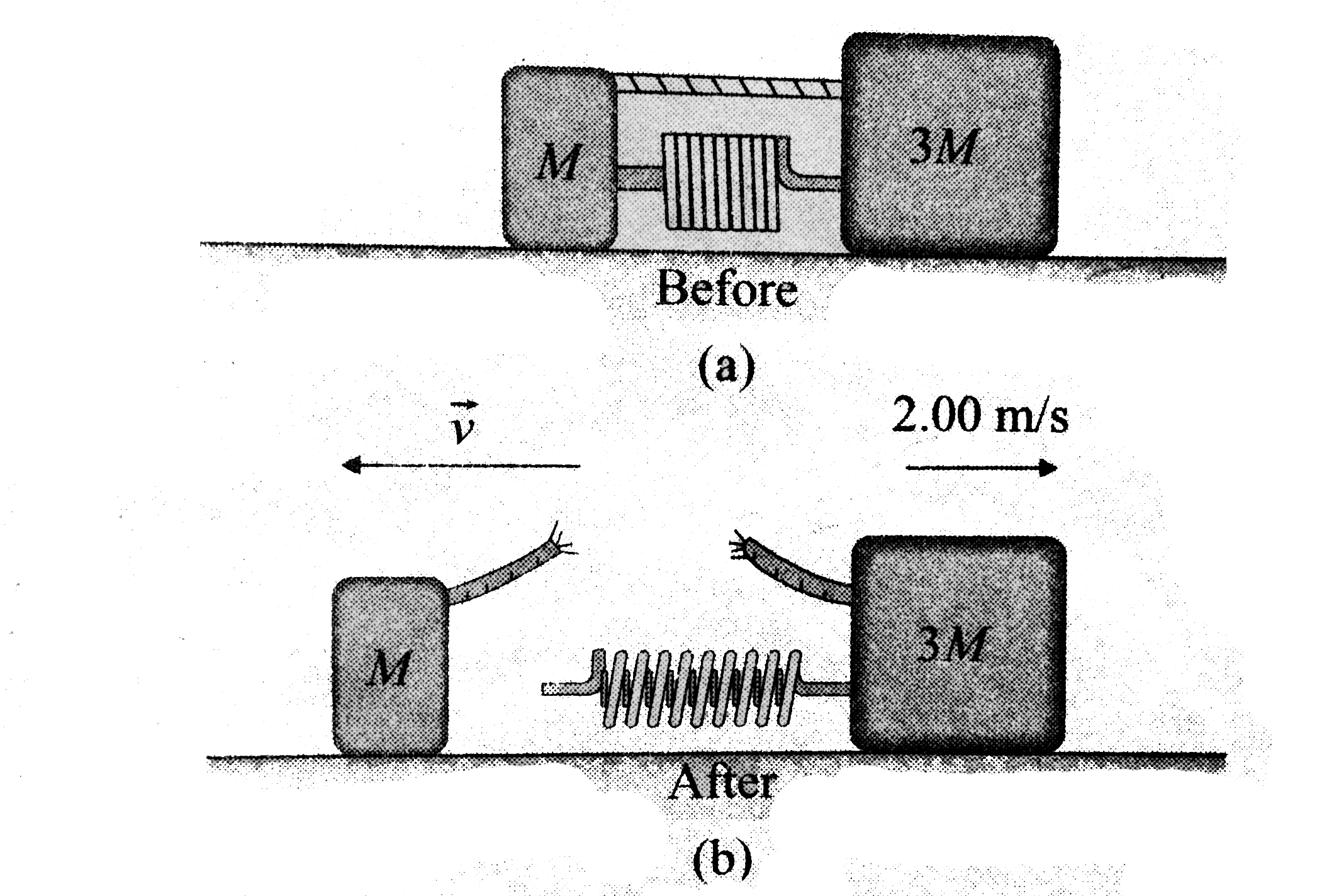
View SolutionTwo blocks of masses M and 3M are placed on a horizontal, frictionless surface. A light spring is attached to one of them and the blocks are pushed together with the spring between them. A cord initially holding the blocks together is burned, after that, the block of mass 3M moves to the right with a speed of 2.00m/s. (a) What is the velocity of the block of mass M. (b) Find the system's original elastic potential energy, taking M=0.350kg. (c) Is the original energy in the spring or in the cord? Explain your answer. (d) Is momentum of the system conserved in the bursting apart process? How can it be with large forces acting? How can it be with no motion beforehand and plenty of motion afterward?
View Solution

