Pressure gradient in the horizontal direction in a static fluid is represented by (z-direction is vertically upwards, and x-axis is along horizontal, d is density of fluid):
∂p∂z=−dg
∂p∂x=dg
∂p∂x=0
∂p∂z=0
The correct Answer is:C
To solve the problem of finding the pressure gradient in the horizontal direction in a static fluid, we can follow these steps:
1. Understand the Concept of Static Fluid:
- A static fluid is one that is not in motion. This means that there are no velocity gradients within the fluid, and the fluid is at rest.
2. Identify the Direction of Interest:
- The question specifically asks about the pressure gradient in the horizontal direction. We will denote the horizontal direction as the x-axis.
3. Apply Pascal's Law:
- According to Pascal's law, in a static fluid, pressure at any point is the same in all directions. Therefore, if we consider any two points in the horizontal direction (along the x-axis), the pressure at these two points will be equal.
4. Define Pressure Gradient:
- The pressure gradient in the x-direction is defined mathematically as the derivative of pressure with respect to x, denoted as ∂P∂x.
5. Evaluate the Pressure Gradient:
- Since the pressure is constant throughout the fluid in the horizontal direction (due to the fluid being static), the change in pressure with respect to x is zero. Thus, we have:
∂P∂x=0
6. Conclusion:
- Therefore, the pressure gradient in the horizontal direction in a static fluid is represented by:
∂P∂x=0
- This indicates that there is no change in pressure along the horizontal direction.
Final Answer:
The pressure gradient in the horizontal direction in a static fluid is represented by ∂P∂x=0.
- A static fluid is one that is not in motion. This means that there are no velocity gradients within the fluid, and the fluid is at rest.
- The question specifically asks about the pressure gradient in the horizontal direction. We will denote the horizontal direction as the x-axis.
- According to Pascal's law, in a static fluid, pressure at any point is the same in all directions. Therefore, if we consider any two points in the horizontal direction (along the x-axis), the pressure at these two points will be equal.
- The pressure gradient in the x-direction is defined mathematically as the derivative of pressure with respect to x, denoted as ∂P∂x.
- Since the pressure is constant throughout the fluid in the horizontal direction (due to the fluid being static), the change in pressure with respect to x is zero. Thus, we have:
∂P∂x=0
- Therefore, the pressure gradient in the horizontal direction in a static fluid is represented by:
∂P∂x=0
- This indicates that there is no change in pressure along the horizontal direction.
The pressure gradient in the horizontal direction in a static fluid is represented by ∂P∂x=0.
Topper's Solved these Questions
- FLUID MECHANICSBook:RESONANCE ENGLISHChapter:FLUID MECHANICSExercise:Examples
Explore 22 Videos
- FLUID MECHANICSBook:RESONANCE ENGLISHChapter:FLUID MECHANICSExercise:Board Level Exercise
Explore 18 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise
Explore 52 Videos
- FULL TEST 1Book:RESONANCE ENGLISHChapter:FULL TEST 1Exercise:Exercise
Explore 30 Videos
Similar Questions
Find the direction cosines of x, y and z-axis.
View SolutionFind the direction cosines of x, y and z-axis.
View SolutionAt a height of 15 m from ground velocity of a projectile is v=(10ˆi+10ˆj). Here ˆj is vertically upwards and ˆi is along horizontal direction then (g = 10 ms−1)
View SolutionA particle having a mass of 10−2kg carries a charge of 5×10−8C. The particle is given an initial horizontal velocity of 105msec−1 in the presence of electric field →E and magnetic field →B. To keep the particle moving in a horizontal direction, it is necessary that
A. →B should be perpendicular to the direction of velocity and →E should be along the direction of velocity
B. Both →B and →E should be along the direction of velocity
C. Both →B and →E are mutually perpendicular and perpendicular to the direction of velocity
D. →B should be along the direction of velocity and →E should be perpendicular to the direction of velocity
View SolutionA simple pendulum is oscillating in a trolley moving on a horizontal straight road with constant acceleration a. If direction of motion of trolley is taken as positive x direction and vertical upward direction as positive y direction then the mean position of pendulum makes an angle
View SolutionAssertion: All surfaces shown in figure are smooth. System is released from rest. Momentum of system in horizontal direction is constant but overall momentum is not constant.
Reason: A net vertically upward force is acting on the system.
View SolutionA particle is released from rest from origin O. There is a uniform magnetic field in negative z-direction. Positive y-direction is vertically upwards. After falling through 5m the velocity vector makes an angle 30∘ with x-axis.

Find the correct option
View SolutionA particle is released from rest from origin O. There is a uniform magnetic field in negative z-direction. Positive y-direction is vertically upwards. After falling through 5m the velocity vector makes an angle 30∘ with x-axis.

The path of the particle is
View SolutionTwo graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
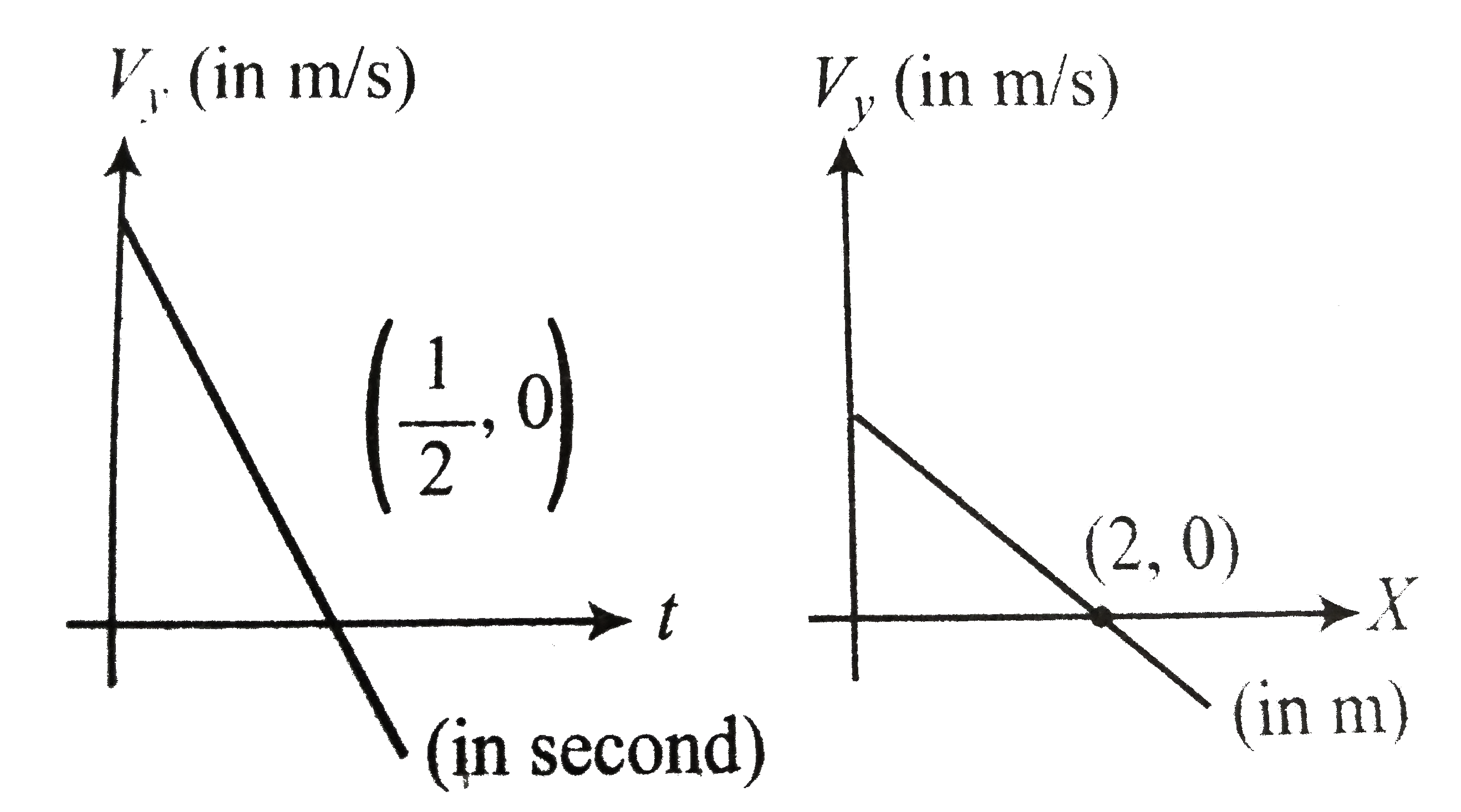
Projection angle with the horizontal is :
View SolutionA rectangular container moves with an acceleration a along the positive direction as shown in figure. The pressure at the A in excess of the atmospheric pressure p0 is (take ρ as the density of liquid)

View Solution

