For adiabatic process of an ideal gas the value of dPP is equals to
−γdVV
−γVdV
dVV
−γ2dVV
The correct Answer is:A
To find the value of dPP for an adiabatic process of an ideal gas, we can follow these steps:
Step 1: Understand the Adiabatic Process
In an adiabatic process, the relationship between pressure P, volume V, and the adiabatic index γ (which is the ratio of specific heats Cp/Cv) is given by:
PVγ=k
where k is a constant.
Step 2: Differentiate the Adiabatic Condition
We differentiate the equation PVγ=k with respect to V:
ddV(PVγ)=0
Using the product rule, we have:
dP⋅Vγ+P⋅γVγ−1⋅dV=0
Step 3: Rearranging the Equation
From the differentiated equation, we can isolate dP:
dP⋅Vγ=−P⋅γVγ−1⋅dV
Now, we can solve for dPP:
dPP=−γVγ−1VγdV
Step 4: Simplifying the Expression
This simplifies to:
dPP=−γdVV
Final Result
Thus, the value of dPP for an adiabatic process of an ideal gas is:
dPP=−γdVV
In an adiabatic process, the relationship between pressure P, volume V, and the adiabatic index γ (which is the ratio of specific heats Cp/Cv) is given by:
PVγ=k
where k is a constant.
We differentiate the equation PVγ=k with respect to V:
ddV(PVγ)=0
Using the product rule, we have:
dP⋅Vγ+P⋅γVγ−1⋅dV=0
From the differentiated equation, we can isolate dP:
dP⋅Vγ=−P⋅γVγ−1⋅dV
Now, we can solve for dPP:
dPP=−γVγ−1VγdV
This simplifies to:
dPP=−γdVV
Thus, the value of dPP for an adiabatic process of an ideal gas is:
dPP=−γdVV
Topper's Solved these Questions
Similar Questions
Knowledge Check
In an adiabatic expansion of an ideal gas -
A(a) W=−ΔUB(b) W=ΔUC(c) ΔU=0D(d) W=0Assertion : In an adiabatic process, change in internal energy of a gas is equal to work done on/by the gas in the process.
Reason : This is because temp.of gas remains constant in an adiabatic process.AIf both assetion and reason are true and reaasons is the correct expanation of assetionBIf both assetion and reason are tur but reason is not the correct explanation of assetionCIf assertion is true but reason is falseDIf both assertion and reason are false.
The curves A and B in the figure shown P-V graphs for an isothermal and an adiabatic process for an idea gas. The isothermal process is represented by the curve A.
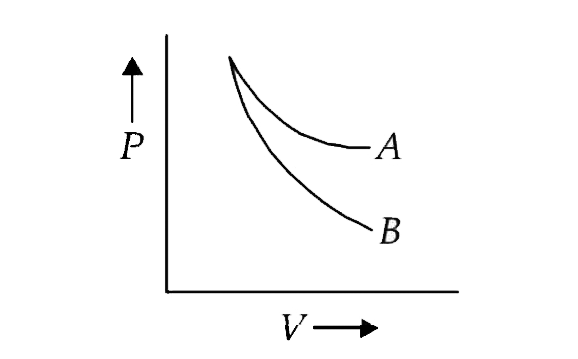
View SolutionThe curves A and B in the figure shown P-V graphs for an isothermal and an adiabatic process for an idea gas. The isothermal process is represented by the curve A.

View SolutionStatement-1 : In an adiabatic process, change in internal energy of a gas is equal to work done on/by the gas in the process.
Statement-2 : This is because temp.of gas remains constant in an adiabatic process.
View SolutionFigure shows the adiabatic curve for n moles of an ideal gas, the bulk modulus for the gas corresponding to the point P will be

View SolutionFigure shows the adiabatic curve for n moles of an ideal gas, the bulk modulus for the gas corresponding to the point P will be

View SolutionFor an adiabatic expansion of an ideal gas the fractional change in its pressure is equal to
View Solution
