The amount of heat given to a system in a cyclic thermodynamical process-
is completely changed with work
is completely changed into internal energy
Brings about reduction in temperature
Brings about increases in temperature
The correct Answer is:A
To solve the question regarding the amount of heat given to a system in a cyclic thermodynamical process, we can follow these steps:
1. Understanding the Cyclic Process:
- In a cyclic thermodynamic process, the system returns to its initial state after completing the cycle. This means that all thermodynamic properties such as pressure, volume, and temperature are the same at the beginning and the end of the process.
2. Applying the First Law of Thermodynamics:
- The first law of thermodynamics states that the change in internal energy (ΔU) of a system is equal to the heat added to the system (Q) minus the work done by the system (W):
ΔU=Q−W
3. Internal Energy in a Cyclic Process:
- Since the initial and final states are the same in a cyclic process, the change in internal energy (ΔU) is zero:
ΔU=0
4. Relating Heat and Work:
- Substituting ΔU = 0 into the first law equation gives:
0=Q−W⟹Q=W
- This means that the total amount of heat given to the system is completely converted into work done by the system.
5. Conclusion:
- Therefore, in a cyclic process, the amount of heat given to the system is equal to the work done by the system, and there is no change in internal energy.
Final Answer:
- The correct statement is that the amount of heat given to the system is completely converted into work done by the system.
- In a cyclic thermodynamic process, the system returns to its initial state after completing the cycle. This means that all thermodynamic properties such as pressure, volume, and temperature are the same at the beginning and the end of the process.
- The first law of thermodynamics states that the change in internal energy (ΔU) of a system is equal to the heat added to the system (Q) minus the work done by the system (W):
ΔU=Q−W
- Since the initial and final states are the same in a cyclic process, the change in internal energy (ΔU) is zero:
ΔU=0
- Substituting ΔU = 0 into the first law equation gives:
0=Q−W⟹Q=W
- This means that the total amount of heat given to the system is completely converted into work done by the system.
- Therefore, in a cyclic process, the amount of heat given to the system is equal to the work done by the system, and there is no change in internal energy.
- The correct statement is that the amount of heat given to the system is completely converted into work done by the system.
Topper's Solved these Questions
Similar Questions
consider the following two statements.
(A) If heat is added to a system, its temperature must increase.
(b) if positive work is done by a system in a thermodynamic process, its volume must increase.
View SolutionA certain amount of an ideal monoatomic gas undergoes a thermodynamic process such that VT2= constat where V= volume of gas, T= temperature of gas. Then under process
View Solution
Knowledge Check
In the P-V diagram (Fig 15.14.1) given below, three thermodynamic processes occur for an ideal gas. Processes 1→2,2→3and3→1 are isothermal, isochoric and adiabatic processes respectively. The total amt of work done is 10 J. During the process 3→1, 20 J of work is done on the system. The amount of heat added to the system during the process 1→2 is
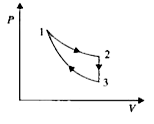 A30 JB20 JC10 JD0 J
A30 JB20 JC10 JD0 J
An ideal gas is taken through a cyclic thermodynamics process through four steps. The amount of heat given to the system in these steps are Q1=1000J, Q2=−800J, Q3=450J, Q4=−200J respectively. The efficiency of cycle is nearly
View SolutionIf ΔU and ΔW represent the increase in internal energy and work done by the system resectively in a thermodynamical process, which of the following is true?
View SolutionIf W is the amount of work done by the system and q is the amount of heat supplied to the system, identify the type of the system
View SolutionIf Q amount of heat is given to a diatomic ideal gas in a process in which the gas perform a work 2Q3 on its surrounding. Find the molar heat capacity (in terms of R) for the process.
View SolutionState true or false, internal energy of a gaseous system depends upon thermodynamic process.
View SolutionLet Q and W denote the amount of heat given to an ideal gas the work done by it in an isothermal process.
View SolutionOne mole of an ideal monoatomic gas is taken through the thermodynamic process shown in the P−V diagram. The heat supplied to the system is
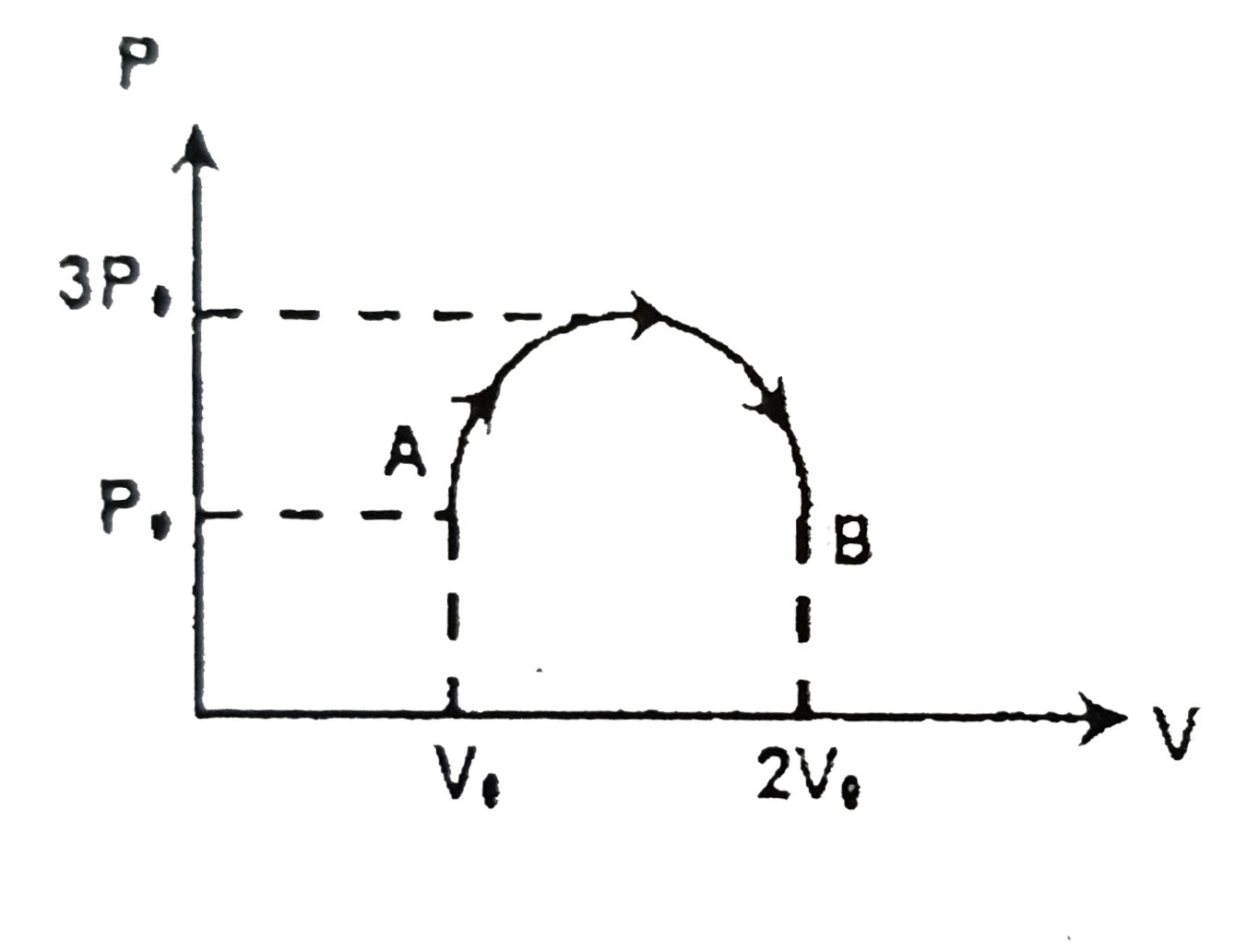
View Solution

