One mass m is suspended from a spring. Time period of oscilation is T. now if spring is divided into n pieces & these are joined in parallel order then time period of oscillation if same mass is suspended.
2π√n2mk
2π√n2km
2π√mn2k
2π√kn2m
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the Initial Time Period
The time period T of a mass m suspended from a spring with spring constant k is given by the formula:
T=2π√mk
Step 2: Analyze the Spring After Cutting
When the spring is cut into n equal pieces, the length of each piece becomes Ln. The spring constant k′ of each piece can be derived from the relationship between the spring constant and the length of the spring. The product of the length and spring constant remains constant:
L⋅k=(Ln)⋅k′
From this, we can solve for k′:
k′=n⋅k
Step 3: Determine the Effective Spring Constant
When these n springs are joined in parallel, the effective spring constant keff is the sum of the spring constants of each piece:
keff=k′+k′+…+k′(n times)
This simplifies to:
keff=n⋅k′=n⋅(n⋅k)=n2⋅k
Step 4: Calculate the New Time Period
Now, we can find the new time period T′ when the mass m is suspended from the new effective spring constant keff:
T′=2π√mkeff=2π√mn2k
This can be simplified to:
T′=2πn√mk
Step 5: Relate the New Time Period to the Original Time Period
Since the original time period T is 2π√mk, we can express T′ in terms of T:
T′=Tn
Final Answer
Thus, the new time period of oscillation when the spring is divided into n pieces and joined in parallel is:
T′=Tn
The time period T of a mass m suspended from a spring with spring constant k is given by the formula:
T=2π√mk
When the spring is cut into n equal pieces, the length of each piece becomes Ln. The spring constant k′ of each piece can be derived from the relationship between the spring constant and the length of the spring. The product of the length and spring constant remains constant:
L⋅k=(Ln)⋅k′
From this, we can solve for k′:
k′=n⋅k
When these n springs are joined in parallel, the effective spring constant keff is the sum of the spring constants of each piece:
keff=k′+k′+…+k′(n times)
This simplifies to:
keff=n⋅k′=n⋅(n⋅k)=n2⋅k
Now, we can find the new time period T′ when the mass m is suspended from the new effective spring constant keff:
T′=2π√mkeff=2π√mn2k
This can be simplified to:
T′=2πn√mk
Since the original time period T is 2π√mk, we can express T′ in terms of T:
T′=Tn
Thus, the new time period of oscillation when the spring is divided into n pieces and joined in parallel is:
T′=Tn
Topper's Solved these Questions
Similar Questions
The time period of small oscillations of mass m :-
_S01_040_Q01.png)
View SolutionOne body is suspended from a spring of length l, spring constant k and has time period T, Now if spring is divided in two equal parts which are joined in paralled and the same body is suspended from this arrangements then determine new time period.
View Solution
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations is
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionA mass m is suspended from a spring of force constant k. The period of oscillation is T0 The spring is cut into 4 equal parts: The same mass m is suspended from one of the parts. What is the new period?
View SolutionAn object suspended from a spring exhibits oscillations of period T. Now the spring is cut in two halves and the same object is suspended with two halves as shown in figure. The new time period of oscillation will become
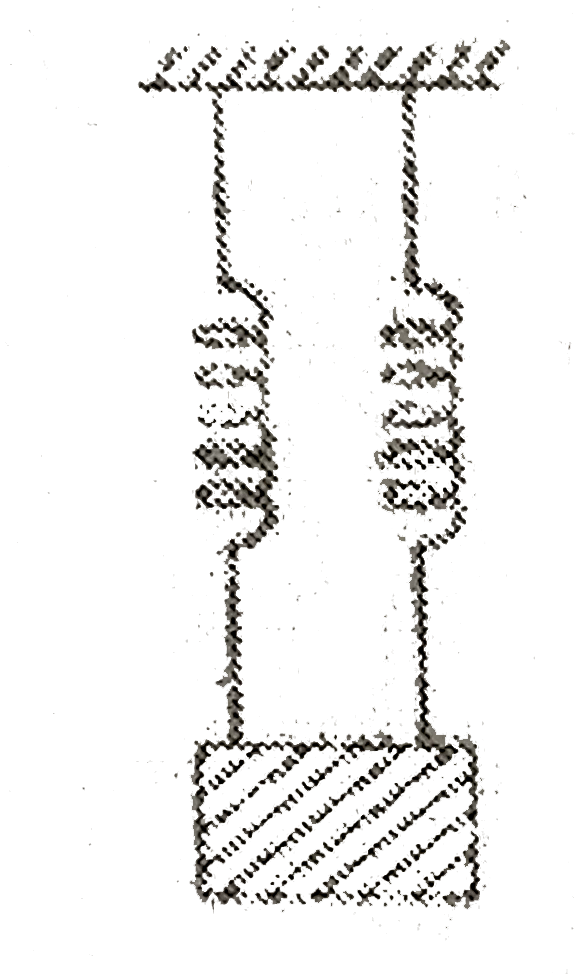
View SolutionA block of mass M suspended from a spring oscillates with time period T. If spring is cut in to two equal parts and same mass M is suspended from one part, new period os oscillation is
View SolutionA block of mass M suspended from a spring oscillates with time period T. If spring is cut in to two equal parts and same mass M is suspended from one part, new period os oscillation is
View SolutionA spring has a certain mass suspended from it and its period for vertical oscillations is T1. The spring is now cut into two equal halves and the same mass is suspended from one of the half. The period of vertical oscillation is now T2. The ratio of T2/T1 is
View SolutionAn object suspended from a spring exhibits oscillations of period T. Now ,the spring is cut in half and the two halves are used to support the same object, as shown in figure. The new period of oscillation is .
 .
.
View Solution

