Question

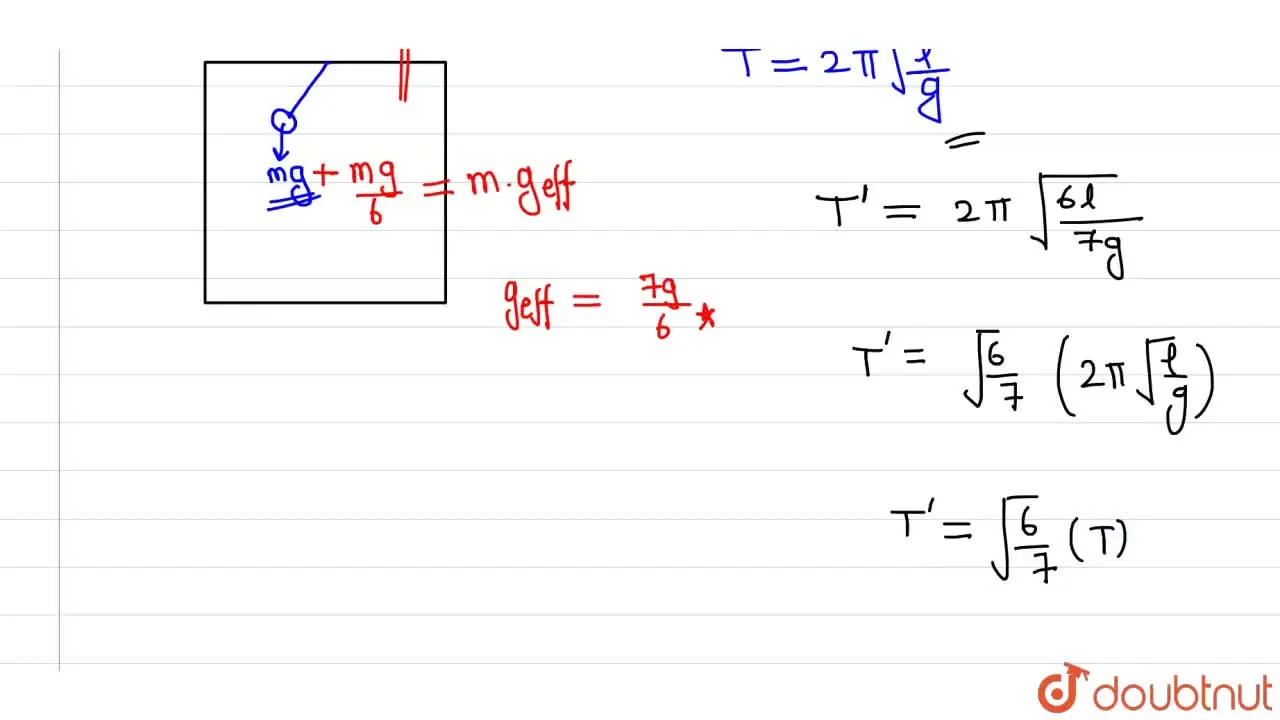
A man measures the period of a simple pendulum inside a stationary lift and finds it to be T sec. if the lift accelerates upwards with an acceleration g/6, then the period of the pendulum will be

Options

A. `T`
B. `T/4`
C. `(2T)/(sqrt(5))`
D. `2Tsqrt(5)`

Answer

C

Explanation

To solve the problem of finding the period of a simple pendulum in an upward-accelerating lift, we can follow these steps:

1. Identify the Initial Conditions:
- When the lift is stationary, the period of the pendulum is given as \( T \) seconds.
- The formula for the period of a simple pendulum is:
\( T = 2\pi \sqrt{\frac{L}{g}} \)
where \( L \) is the length of the pendulum and \( g \) is the acceleration due to gravity.

2. Determine the Effective Gravity When the Lift Accelerates Upwards:
- When the lift accelerates upwards with an acceleration of \( \frac{g}{6} \), the effective acceleration due to gravity (\( g_{\text{effective}} \)) experienced by the pendulum is the sum of the gravitational acceleration and the lift's acceleration:
\( g_{\text{effective}} = g + \frac{g}{6} \)
- To combine these, we can express \( g \) as \( \frac{6g}{6} \):
\( g_{\text{effective}} = \frac{6g}{6} + \frac{g}{6} = \frac{7g}{6} \)

3. Calculate the New Period of the Pendulum:
- The new period \( T' \) of the pendulum in the accelerating lift can be calculated using the modified effective gravity:
\( T' = 2\pi \sqrt{\frac{L}{g_{\text{effective}}}} = 2\pi \sqrt{\frac{L}{\frac{7g}{6}}} \)
- This simplifies to:
\( T' = 2\pi \sqrt{\frac{6L}{7g}} \)

4. Relate the New Period to the Original Period:
- We know that the original period \( T \) is:
\( T = 2\pi \sqrt{\frac{L}{g}} \)
- We can express \( T' \) in terms of \( T \):
\( T' = \sqrt{\frac{6}{7}} \cdot T \)

5. Final Result:
- Therefore, the period of the pendulum when the lift accelerates upwards with an acceleration of \( \frac{g}{6} \) is:
\( T' = T \sqrt{\frac{6}{7}} \)

Summary:
The period of the pendulum when the lift accelerates upwards with an acceleration of \( \frac{g}{6} \) is given by:
\( T' = T \sqrt{\frac{6}{7}} \)