A body is projected up along the rough inclined plane from the bottom with some velocity. It travels up the incline and then returns back. If the time of ascent is ta and time of descent is td then
ta=td
ta>tb
ta<td
data insufficient
The correct Answer is:C
To solve the problem, we need to analyze the motion of a body projected up a rough inclined plane and the forces acting on it during ascent and descent.
1. Identify Forces Acting on the Body During Ascent:
- When the body is projected upwards along the inclined plane, two forces act against its motion:
- The component of gravitational force acting down the incline: Fg=mgsinθ
- The frictional force acting down the incline: Ff=μN (where N=mgcosθ is the normal force and μ is the coefficient of friction).
- Therefore, the total force opposing the motion while ascending is:
Ftotal, ascent=mgsinθ+μmgcosθ
2. Apply Newton's Second Law for Ascent:
- According to Newton's second law, the net force acting on the body is equal to the mass times acceleration:
ma=−(mgsinθ+μmgcosθ)
- This can be simplified to:
a=−g(sinθ+μcosθ)
3. Determine Time of Ascent ta:
- Using the kinematic equation v2=u2+2as, where v=0 (final velocity at the highest point), u is the initial velocity, and s is the distance traveled up the incline:
0=u2−2g(sinθ+μcosθ)s
- Rearranging gives:
s=u22g(sinθ+μcosθ)
- The time of ascent ta can be found using t=ua:
ta=ug(sinθ+μcosθ)
4. Identify Forces Acting on the Body During Descent:
- When the body descends, the forces acting on it are:
- The component of gravitational force acting down the incline: Fg=mgsinθ
- The frictional force acting up the incline: Ff=μmgcosθ
- The total force acting on the body while descending is:
Ftotal, descent=mgsinθ−μmgcosθ
5. Apply Newton's Second Law for Descent:
- Using Newton's second law again:
ma=mgsinθ−μmgcosθ
- This simplifies to:
a=g(sinθ−μcosθ)
6. Determine Time of Descent td:
- Using the same kinematic equation for descent:
v2=0+2as
- The time of descent td can be found using:
td=ug(sinθ−μcosθ)
7. Establish the Relation Between ta and td:
- From the expressions for ta and td:
ta=ug(sinθ+μcosθ)
td=ug(sinθ−μcosθ)
- Comparing these two, we can see that since sinθ+μcosθ>sinθ−μcosθ, it follows that:
td>ta
Final Conclusion:
The time of descent td is greater than the time of ascent ta:
td>ta
- When the body is projected upwards along the inclined plane, two forces act against its motion:
- The component of gravitational force acting down the incline: Fg=mgsinθ
- The frictional force acting down the incline: Ff=μN (where N=mgcosθ is the normal force and μ is the coefficient of friction).
- Therefore, the total force opposing the motion while ascending is:
Ftotal, ascent=mgsinθ+μmgcosθ
- According to Newton's second law, the net force acting on the body is equal to the mass times acceleration:
ma=−(mgsinθ+μmgcosθ)
- This can be simplified to:
a=−g(sinθ+μcosθ)
- Using the kinematic equation v2=u2+2as, where v=0 (final velocity at the highest point), u is the initial velocity, and s is the distance traveled up the incline:
0=u2−2g(sinθ+μcosθ)s
- Rearranging gives:
s=u22g(sinθ+μcosθ)
- The time of ascent ta can be found using t=ua:
ta=ug(sinθ+μcosθ)
- When the body descends, the forces acting on it are:
- The component of gravitational force acting down the incline: Fg=mgsinθ
- The frictional force acting up the incline: Ff=μmgcosθ
- The total force acting on the body while descending is:
Ftotal, descent=mgsinθ−μmgcosθ
- Using Newton's second law again:
ma=mgsinθ−μmgcosθ
- This simplifies to:
a=g(sinθ−μcosθ)
- Using the same kinematic equation for descent:
v2=0+2as
- The time of descent td can be found using:
td=ug(sinθ−μcosθ)
- From the expressions for ta and td:
ta=ug(sinθ+μcosθ)
td=ug(sinθ−μcosθ)
- Comparing these two, we can see that since sinθ+μcosθ>sinθ−μcosθ, it follows that:
td>ta
The time of descent td is greater than the time of ascent ta:
td>ta
Topper's Solved these Questions
Similar Questions
A block is projected upwards on a rough inclined plane at 20 m/s. let the time in going up, then is equal to

View SolutionA body is projected up along an inclined plane from the bottom with speed V1. If it reaches the bottom of the plane with a velocity V2, find (v1/v2) if θ is the angle of inclination with the horizontal and μ be the coefficient of.
View Solution
Knowledge Check
A solid cylinder rolls up an inclined plane of inclination θ with an initial velocity v. How far does the cylinder go up the plane ?
A3v22gsinθBv24gsinθC3v2gsinθD3v24gsinθ
A body is pushed up on a rough inclined plane making an angle 30∘ to the horizontal. If its time of ascent on the plane is half the time of its descent, find coefficient of friction between the body and the incined plane.
View SolutionA block is pushed up a rough inclined plane of 45°. If the time of descent is twice the time of ascent, the coefficient of friction is
View SolutionA body of mass 5×10−3 kg is launched upon a rough inclined plane making an angle of 30∘ with the horizontal. Obtain the coefficient of friction between the body and the plane if the time of ascent is half of the time of descent.
View SolutionA ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time

View SolutionA particle is projected directly along a rough plane of inclination θ with velocity u. If after coming to the rest the particle returns to the starting point with velocity v, the coefficient of friction between the partice and the plane is
View SolutionA body is projected up a smooth inclined plane with velocity V from the point A as shown in the figure. The angle of inclination is 45∘ and the top is connected to a well of diameter 40m. If the body just manages to across the well, what is the value of V? Length of inclined plane is 20√2m.
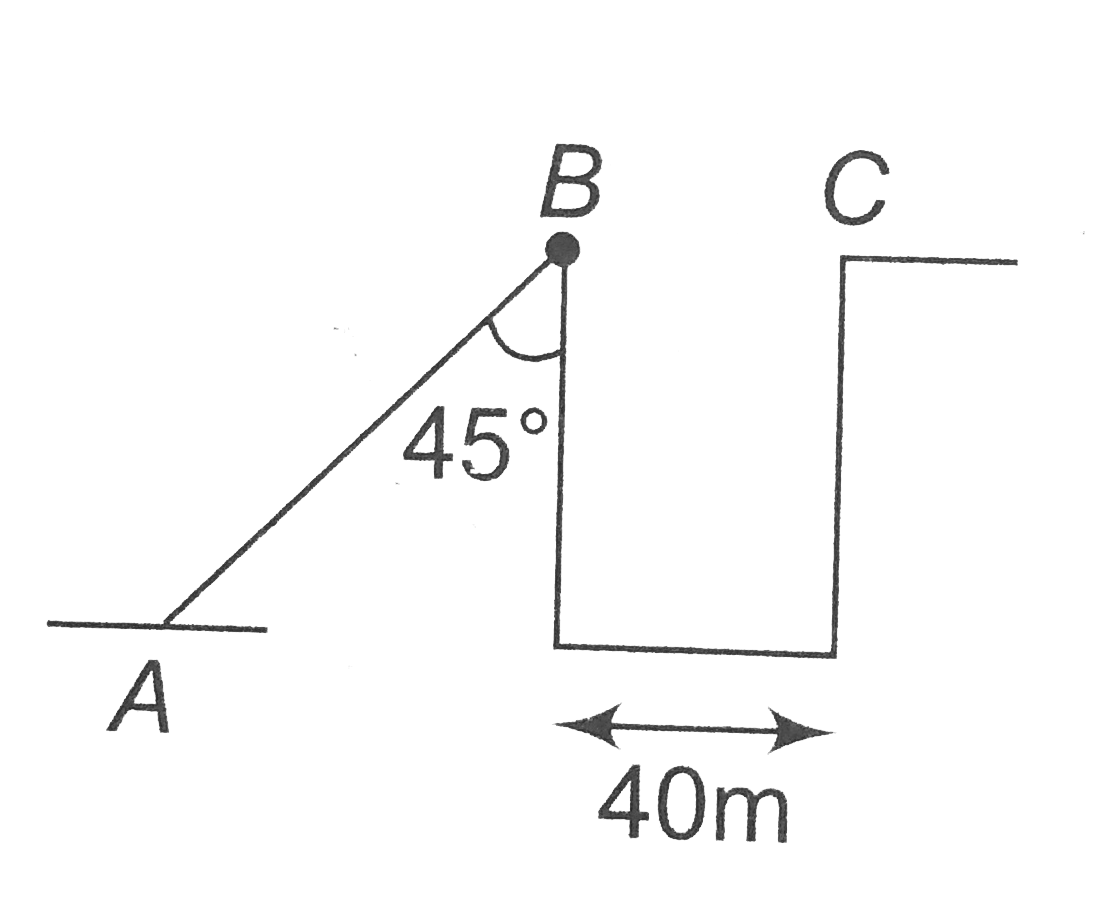
View SolutionAn object in projected up the inclined at the angle shown in the figure with an initial velocity of 30ms−1. The distance x up the incline at which the object lands is
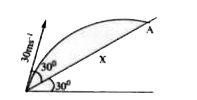
View Solution