A uniform rope so lies on a table that part of it lays over. The rope begins to slide when the length of hanging part is 25% of entire length. The co-efficient of friction between rope and table is
0.33
0.25
0.5
0.2
The correct Answer is:A
To solve the problem step by step, we will analyze the forces acting on the rope and use the concept of friction to find the coefficient of friction between the rope and the table.
1. Understand the Setup:
- A uniform rope is lying on a table, and part of it is hanging off the edge.
- The length of the hanging part is 25% of the total length of the rope.
2. Define Variables:
- Let the total mass of the rope be m.
- The mass of the hanging part (25% of the rope) is m4.
- The mass of the part lying on the table (75% of the rope) is 3m4.
3. Identify Forces:
- The hanging part of the rope experiences a gravitational force pulling it down, which is Fhanging=m4g.
- The part of the rope lying on the table experiences a normal force due to its weight, which is Fnormal=3m4g.
4. Frictional Force:
- The frictional force Ffriction that opposes the motion of the rope is given by:
Ffriction=μFnormal
- Here, μ is the coefficient of friction.
5. Set Up the Equation:
- For the rope to begin sliding, the frictional force must equal the weight of the hanging part:
Ffriction=Fhanging
- Substituting the expressions we have:
μ(3m4g)=m4g
6. Simplify the Equation:
- We can cancel g and m from both sides (assuming g and m are not zero):
μ(34)=14
7. Solve for μ:
- Rearranging gives:
μ=1/43/4=13
8. Final Answer:
- The coefficient of friction μ is 13 or approximately 0.33.
Summary:
The coefficient of friction between the rope and the table is 13 or 0.33.
- A uniform rope is lying on a table, and part of it is hanging off the edge.
- The length of the hanging part is 25% of the total length of the rope.
- Let the total mass of the rope be m.
- The mass of the hanging part (25% of the rope) is m4.
- The mass of the part lying on the table (75% of the rope) is 3m4.
- The hanging part of the rope experiences a gravitational force pulling it down, which is Fhanging=m4g.
- The part of the rope lying on the table experiences a normal force due to its weight, which is Fnormal=3m4g.
- The frictional force Ffriction that opposes the motion of the rope is given by:
Ffriction=μFnormal
- Here, μ is the coefficient of friction.
- For the rope to begin sliding, the frictional force must equal the weight of the hanging part:
Ffriction=Fhanging
- Substituting the expressions we have:
μ(3m4g)=m4g
- We can cancel g and m from both sides (assuming g and m are not zero):
μ(34)=14
- Rearranging gives:
μ=1/43/4=13
- The coefficient of friction μ is 13 or approximately 0.33.
The coefficient of friction between the rope and the table is 13 or 0.33.
Topper's Solved these Questions
Similar Questions
A rope lies on a table such that a part of it hangs down the table, when the length of hanging part is 1/3 of entire length the rope just begins to slide. The coefficient of friction between the rope and the table is:-
View SolutionA uniform chain of mass m and length l is at the verge of sliding under the effect of gravity of the hanging part. Find the

a. coefficient of friction, between chain and table.
b. work done by friction and gravity till the chain leaves the table if the hanging part is pulled gently and released.
c. speed of the chain at the time of leaving the table in part (b) .
d. work done by the external force acting at the end A of the chain in slowly pulling the chain completely onto the table.
View SolutionA rope of length L and mass M is being pulled on a rough horizontal floor by a contact horizontal force F=mg. The force is acting at one end of the rope in the same direction as the length of the rope. The coefficient of kinetic friction between rope and floor is 1/2. Then the tension at the midpoint of the rope is
View Solution
One-fourth length of a uniform rod of mass m and length l is placed on a rough horizontal surface and it is held stationary in horizontal position by means of a light thread as shown in the figure. The thread is then burnt and the rod start rotating about the edge. Find the angle between the rod and the horizontal when it is about to slide on the edge. The coefficient of friction between the rod and surface is μ.
View SolutionA uniform chain of length l is placed on rough table with length l/n (where n>1) , hanging over the edge. If the chain just begins to slide off the table by itself from this position, the coefficient of friction between the chain and the table is
View SolutionA chain is lying on a rough table with a fraction 1/n of its length hanging down from the edge of the table. if it is just on the point of sliding down from the table, then the coefficient of friction between the table and the chain is -
View SolutionA block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of table and from its other end another block B of mass m2 is suspended. The coefficient of knetic friction between the block and table is μk . When the block A is sliding on the table, the tension in the string is.
View SolutionA uniform rope of length l lies on a table . If the coefficient of friction is μ , then the maximum length l1 of the part of this rope which can overhang from the edge of the table without sliding down is :
1μ
lμ+1
μl1+μ
μl1−μ
View SolutionA uniform chain of mass m and length I is kept on the table with a part of it overhanging (see figure). If the coefficient of friction between the table and the chain is 1/3 then find the maximum length of the chain that can overhang such that the chain remain in equilibrium.
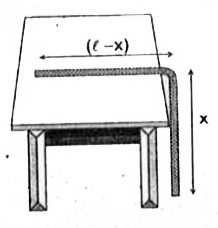
View SolutionA uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

If the chain is limiting equlibrium, what is the coefficient of friction for the contact between table and chain?
View Solution
