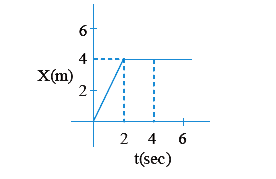
In the figure, the position time graph of a particle of mass 0.1 kg is shown. The impulse at t=2 second is :
0.2gkm/sec
−0.2kgmsec−1
0.1kgmsec−1
−0.1kgm/sec
The correct Answer is:B
Corresponding velocity -time graph is
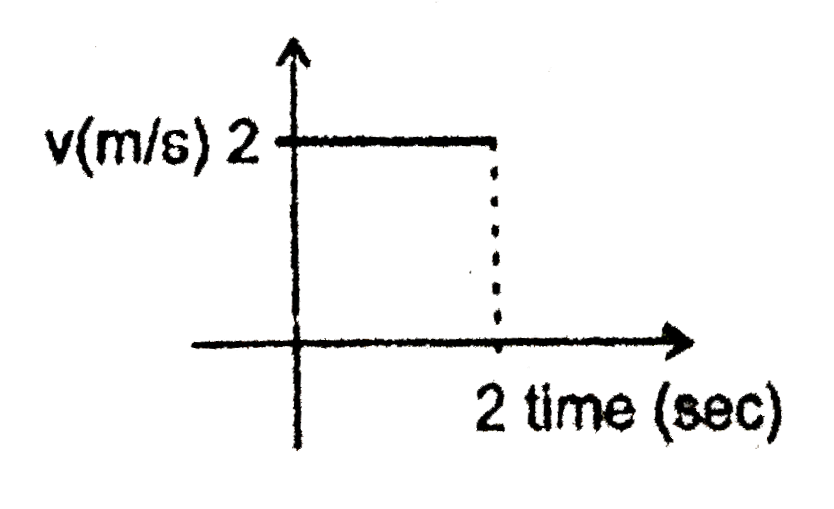
Accordingly, change in momentum at t=2 sec is
Δp=pf−pi=0.1×0−0.1×2=0.2
or impulse =-0.2 kg m/s
Topper's Solved these Questions
Similar Questions
In the figure given below, the position time graph of a particle of mass 0.1kg is shown. The impulse at t=2 sec is
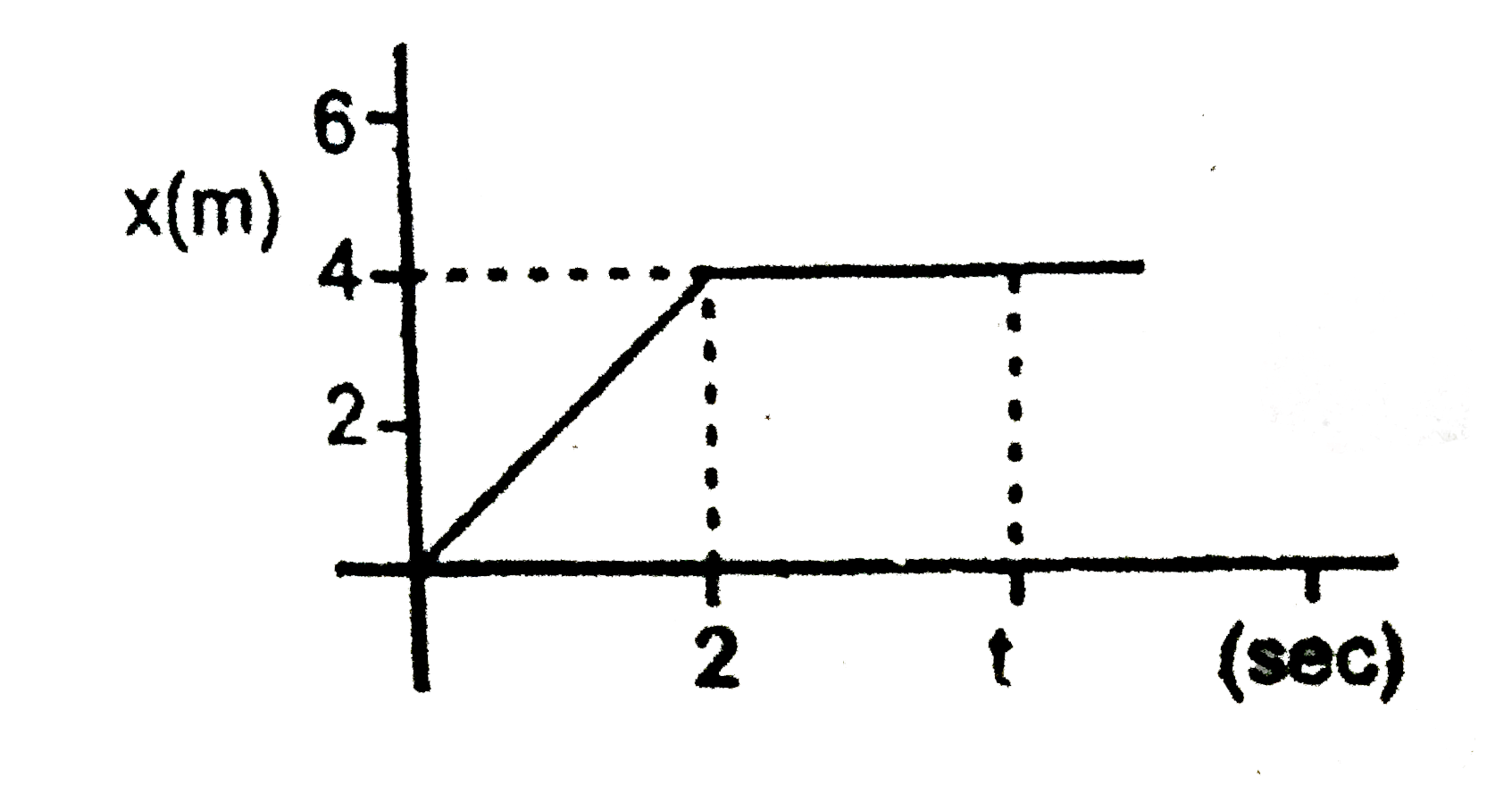
View SolutionIn the figure given below, the position-time graph of a particle of mass 0.1kg is shown. The impuslse at t=2 sec is
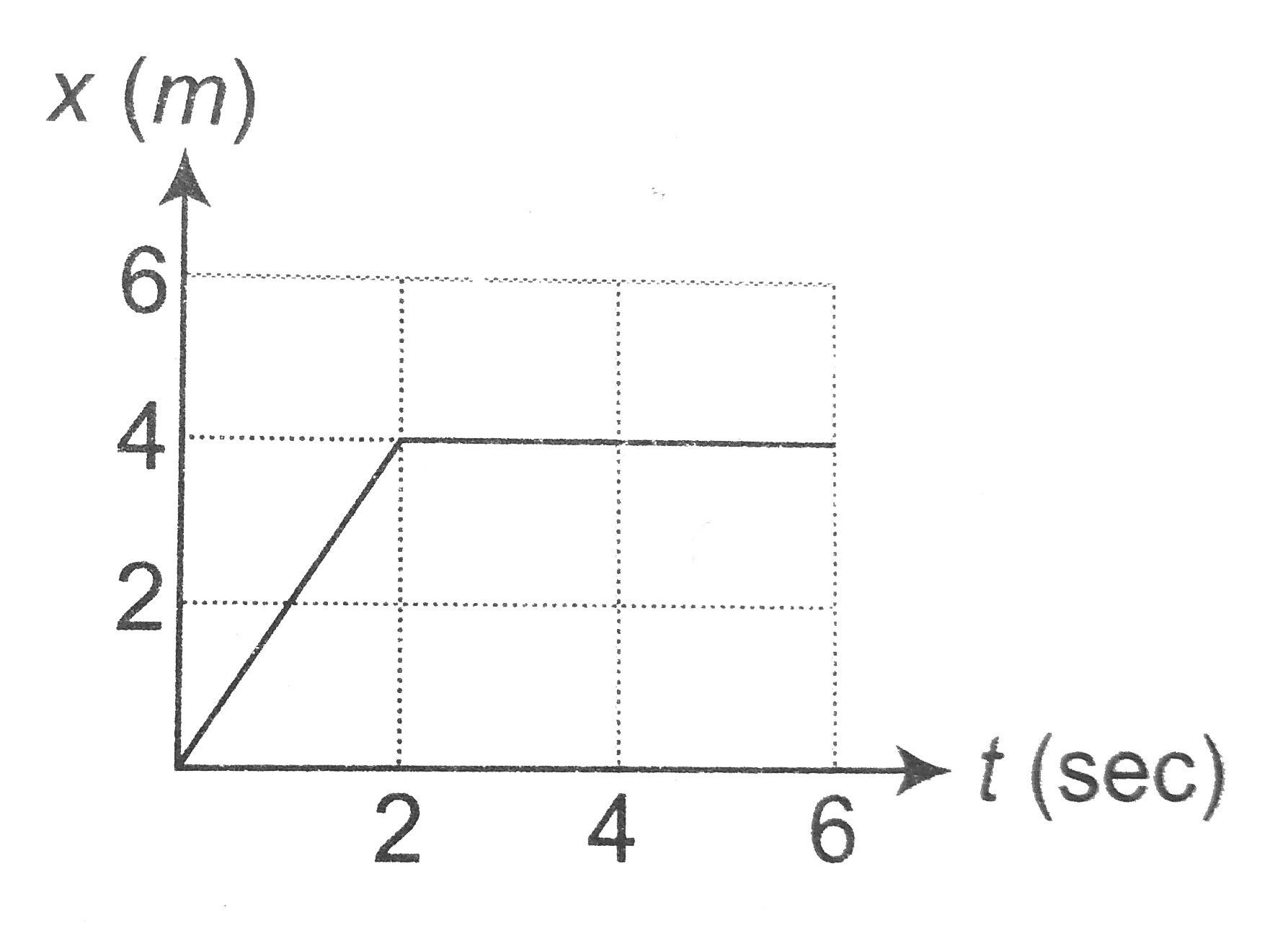
View SolutionThe figure shows the position time graph of a particle of mass 40 kg. What is the force acting on the particle of 0<t<4 s
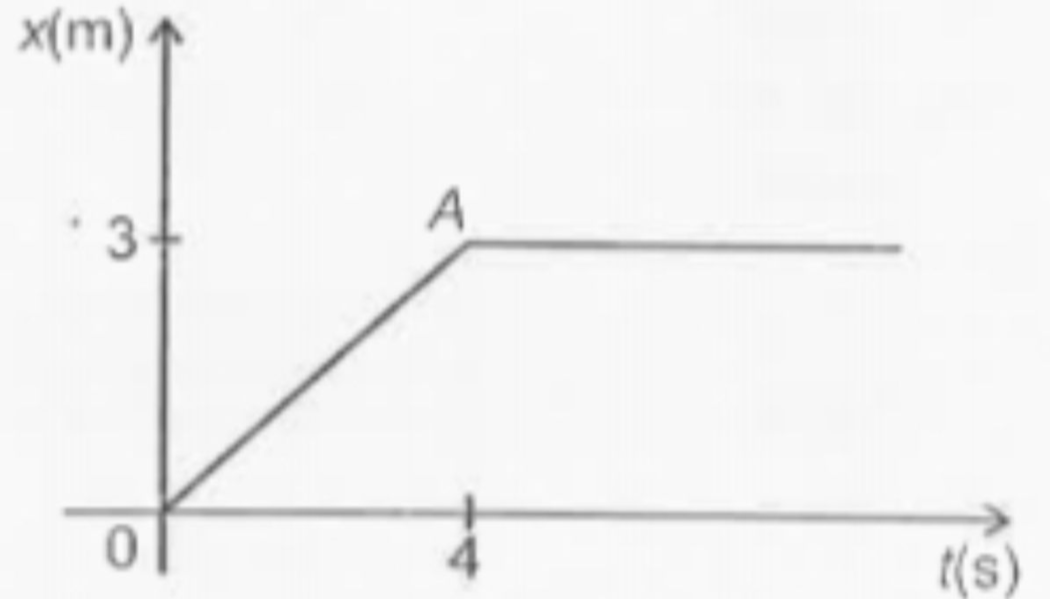
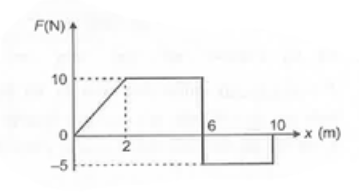
View SolutionThe force versus position (F-x) graph of a particle of mass 2 kg is shown in the figure. If at x = 0 velocity of particle is 2 m/s then velocity of the particle at x = 8 m will be
View SolutionThe velocity − time graph of a particle is as shown in figure

View SolutionFigure shows the position-time graph of a particle of mass 0.04kg. Suggest a suitable physical context for this motion. What is the time between two consecutive impulses received by the particle? What is the magnitude of each impulse?
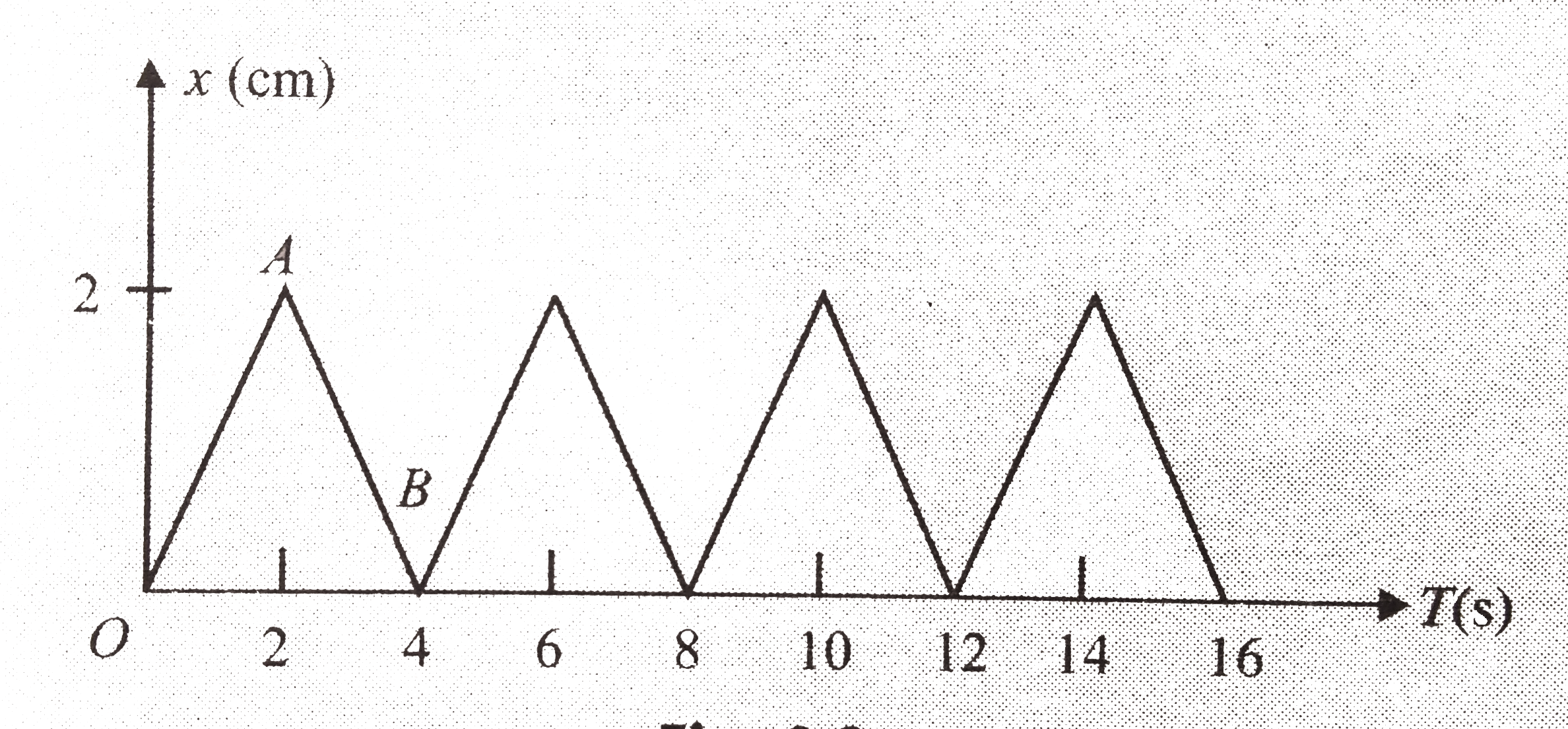
View SolutionFigure shows the position-time graph of a particle of mass 0.04kg. Suggest a suitable physical context for this motion. What is the time between two consecutive impulses received by the particle? What is the magnitude of each impluse?
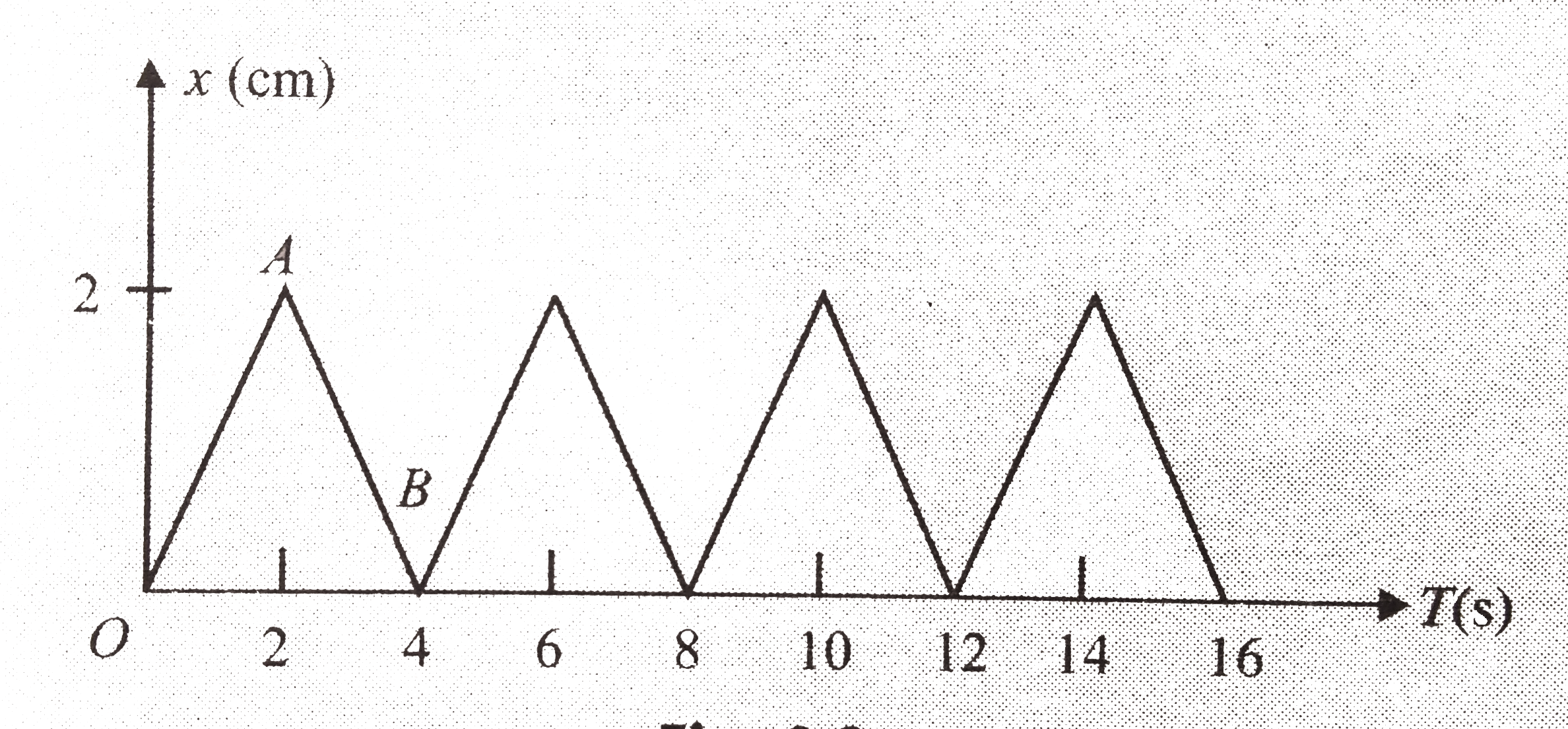
View SolutionIn the figure the variation of components of acceleration of a particle of mass is 1kg is shown w.r.t. time. The initial velocity of the particle is →u=(−3i+4j)m/s. The total work done by the resultant force on the particle in time from t=0 to t=4 seconds is :
 .
.
View SolutionThe position - time graph for a particle is shown in fig. Then in the time interval of (0, 6sec)

View SolutionPosition time graph of a particle of mass 2 kg is shown in figrure. Total work done on the particle from t=0 to t=4s is

View Solution
