The system shown is hanging in equilibrium above the ground. When the string is cut at t=0. The time at which the spring is at its natural length will be (Take π2=10)
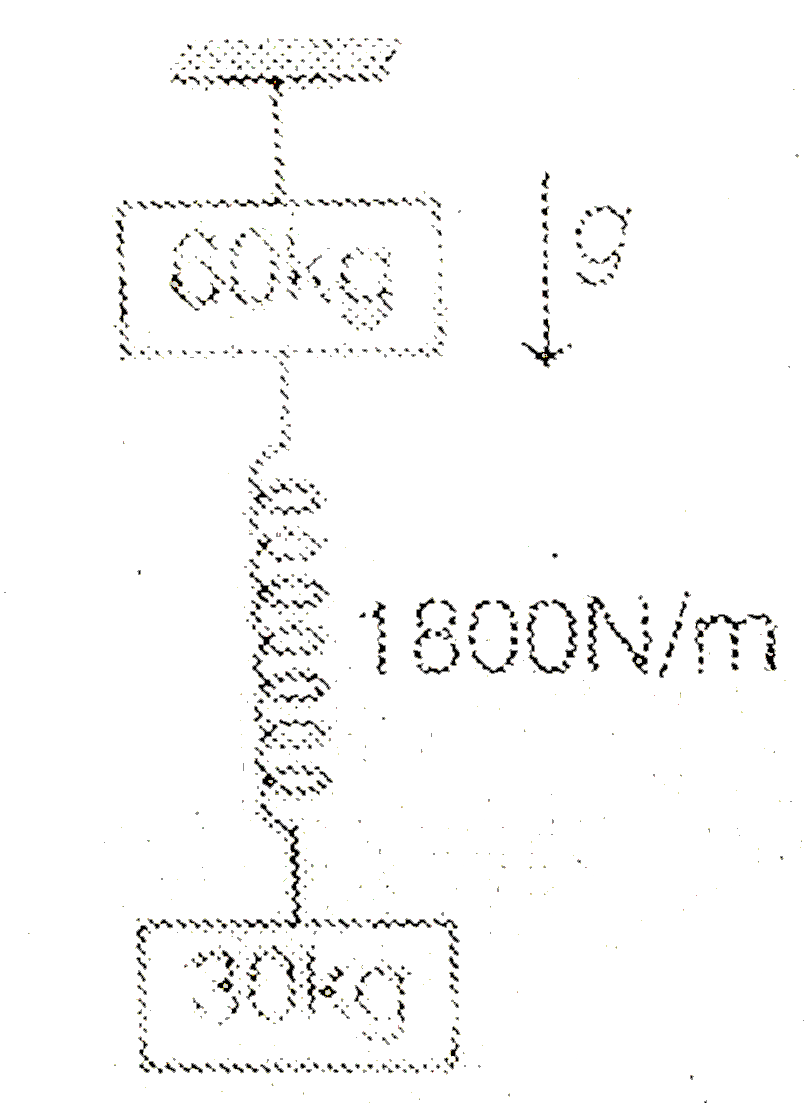
g/2 upwards , g downwards
g upwards, g/2 down wards
g upwards, 2g downwards
2g upwards, g downwards
The correct Answer is:A
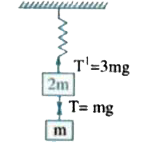
After string is cut, FBD of m
a=mgm=g⏐⏐
⏐↓

FBD of 2m (when string is cut tension in the spring takes finite time to becomes zero. How ever tension in the string immediately become zero.)

a=3mg−2mg2m=g2↑⏐
⏐⏐
Topper's Solved these Questions
Similar Questions
Initially the system shown in figure is in equilibrium. At the moment, the string is cut the downward of a1 and a2 are.
 .
.
View SolutionThe system shown in the figure is in equilibrium at rest. The spring and string are massless Now the string is cut. Find the acceleration of the blocks just after the string is cut.
View SolutionThe system shown in figure is initially in equilibrium. What is the acceleration of B just after the string connecting B to ground is cut ?

View SolutionSystem shown in fig is in equilibrium and at rest. The spring and string are massless now the string is cut. The acceleration of mass 2m and m just after the string is cut will be:

View SolutionSystem shown in fig is in equilibrium and at rest. The spring and string are massless now the string is cut. The acceleration of mass 2m and m just after the string is cut will be:

View SolutionTwo block of mass 2kg are connected by a massless ideal spring of spring contant K=10N/m . The upper block is suspended from roof by a light string A . The system shown is in equilibrium. The string A is now cut, the acceleration of upper block just after the string A is cut will be (g=10m/s2 .

View SolutionTwo block of mass 2kg are connected by a massless ideal spring of spring contant K=10N/m . The upper block is suspended from roof by a light string A . The system shown is in equilibrium. The string A is now cut, the acceleration of upper block just after the string A is cut will be (g=10m/s2 .

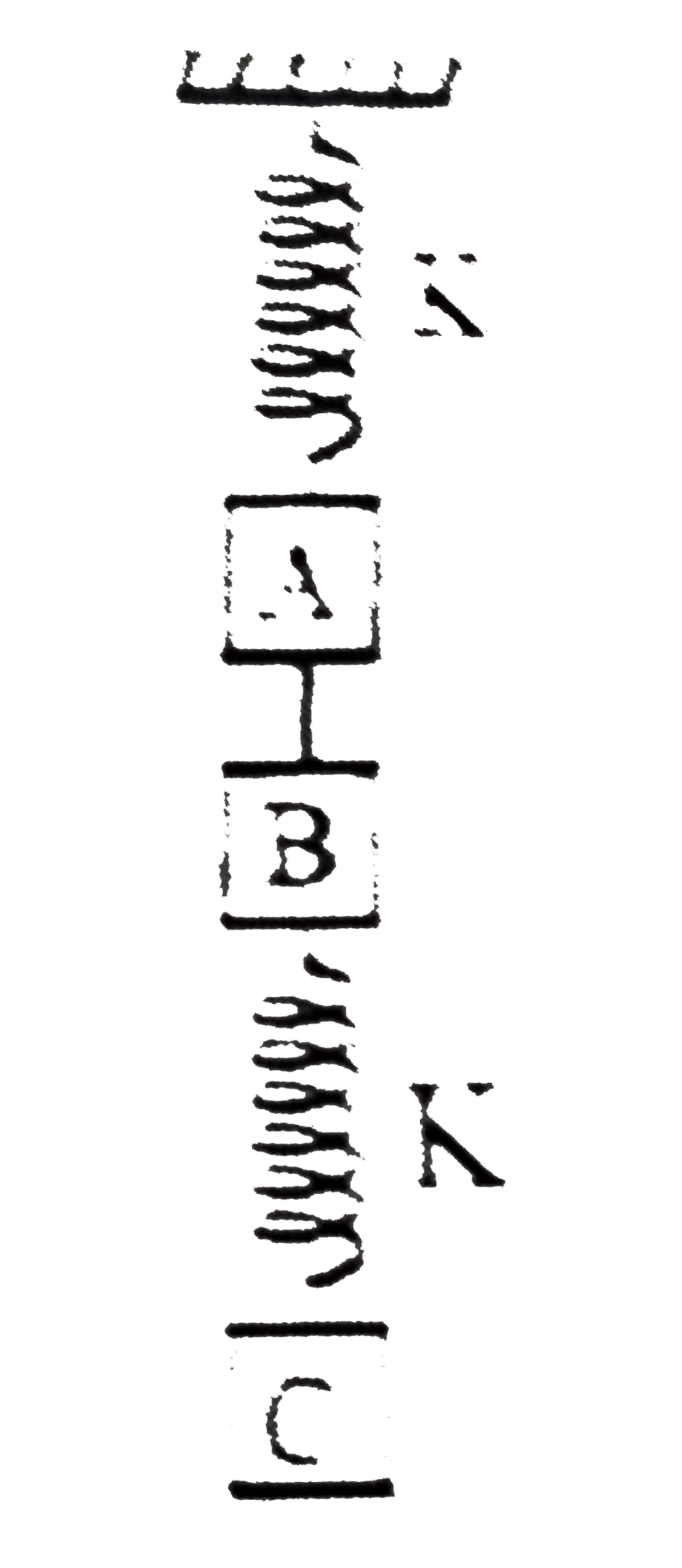
View SolutionThe system shown adjacent is in equilibrium. Find the acceleration of the blocks A,B &C all of equal masses m at the instant when
(Assume springs to be ideal)
(i) The spring between celling & A is cut.
(ii) The spring (inextensible) between A&B is cut.
(iii) The speing between B & C is cut.
Also find the tension in the string when the system is at rest and in the above 3 cases.
View SolutionSystem shown in figure is in equilibrium, find the magnitude of net change in the string tension between two masses just after, when one of the springs in cut, Mass of both the blocks is same and equal to m spring constant of both springs is k.
 .
.
View SolutionSystem shown in figure is in equilibrium, find the magnitude of net change in the string tension between two masses just after, when one of the springs in cut, Mass of both the blocks is same and equal to m spring constant of both springs is k.
 .
.
View Solution
