A particle is resting over a smooth horizontal floor. At t=0, a horizontal force starts acting on it. Magnitude of the force increases with time according to law F=αt, Where alpha is a positive constant. From figure, which of the following statements are correct ? 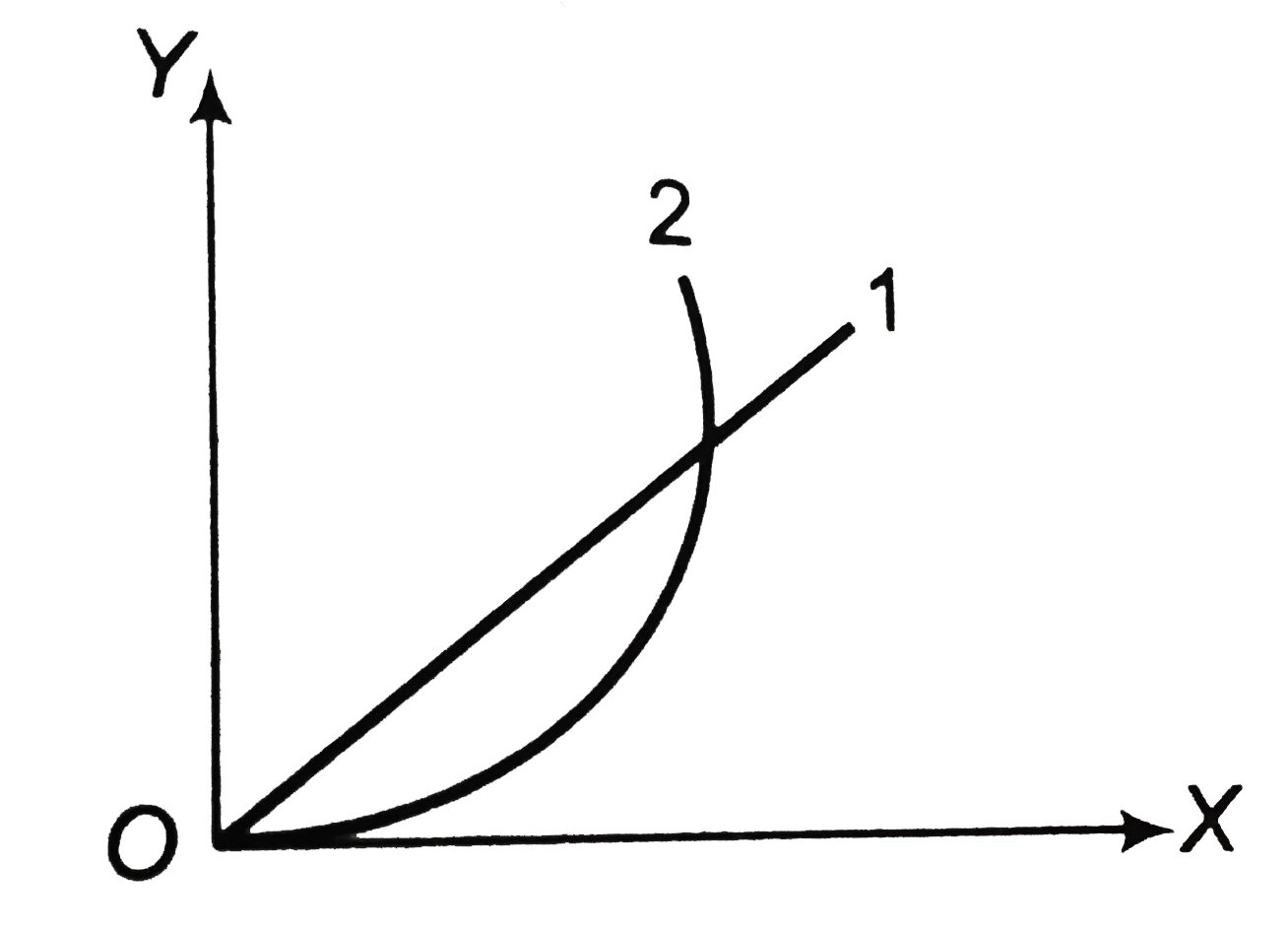
Curve 1 shows acceleration against time
Curve 2 shows velocity against time
Curve 2 shows velocity against acceleration
none of these
The correct Answer is:D
F=αt
ma=αt ⇒aαt
curve 1 is against time mdvdt=∝t.
Integrating this we get v∝t this implise parabola.
also v∝a2⇒ curve 3 shows velocity against acceleration.
Topper's Solved these Questions
Similar Questions
A uniform plank is resting over a smooth horizontal floor and is pulled by applying a horizontal force at its one end. Which of the following statements are not correct?
View SolutionA uniform plank is resting over a smooth horizontal floor and is pulled by applying a horizontal force at its one end. Which of the following statements are not correct?
View SolutionA block is resting over a rough horizontal floor. At t=0 a time -verying force starts acting on it , the force is described by equation F=kt where k is constant and r is in seconds Marks the cerrect statement (s) for this situation .
View SolutionA particle having a velocity v=v0 at t=0 is decelerated at the rate |a|=α√v, where α is a positive constant.
View SolutionA particle is kept at rest at the origin. A constant force →F starts acting on it at t=0. Find the speed of the particle at time t.
View SolutionIf force F is increasing with time and at t=0,F=0, where will slipping first start?

View SolutionTwo particles are shown in figure. At t=0 a constant force F=6N starts acting on 3kg. Find the velocity of circle of mass of these particle at t=5s.
 .
.
View SolutionThe displacement x of a particle varies with time t as x=ae−αt+beβt. Where a,b,α and β positive constant.
The velocity of the particle will.
View SolutionThe displacement x of a particle varies with time t as x=ae−αt+beβt. Where a,b,α and β positive constant.
The velocity of the particle will.
View SolutionA particle moves in the XY-plane according to the law x=kt,y=kt(1−αt), where k and α are positive constants and t is time. The trajectory of the particle is
View Solution
