A particle of mass m is given initial horizontal velocity of magnitude u as shown in the figure. It transfers to the fixed inclined plane without a jump, that is, its trajectory changes sharply from the horizontal line to the inclined line. All the surfaces are smooth adn 90∘≥θ>0∘. Then the height to which the particle shamm rise on the inclined plane (assume the length of the inclined plane to be very large)

increases with increase in θ
decreases with increase in θ
is independent of θ
date insufficient
The correct Answer is:B
Just before the particle transfers to inclined surface, we resolve its velocity along and normal to the plane.
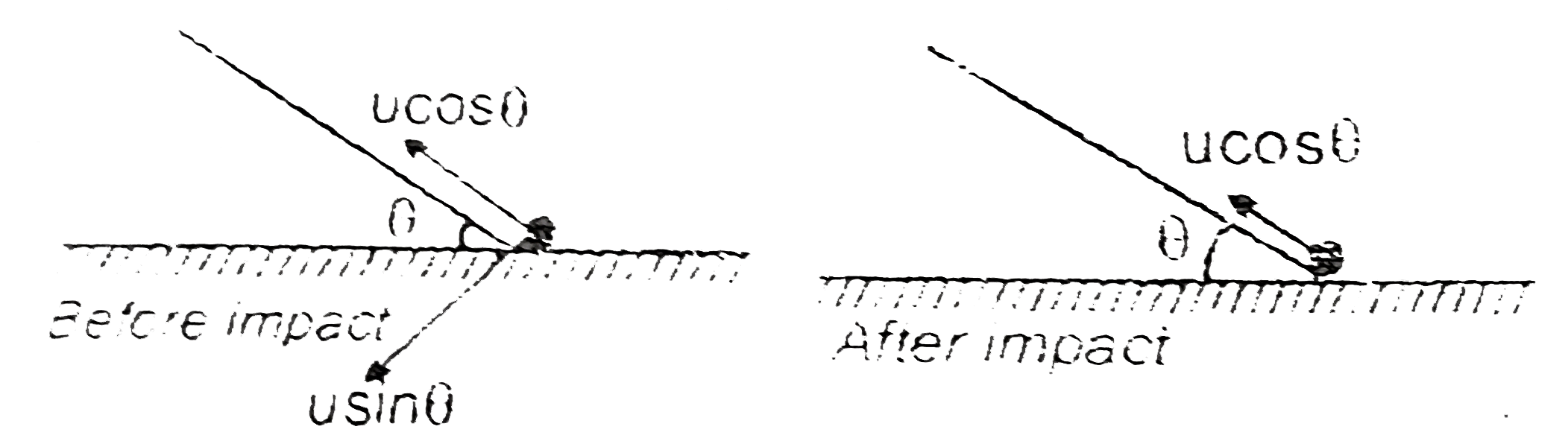
For the trajectory of the particle to sharply change from the horizontal line to the inclined line, the impact of the particle with inclined plane should reduce the usinθ component of velocity to zero. Hence the particle moves up the incline with speed ucosθ.
Hence as θ increases, the height to which the particel rises shall decrease.
Related Playlists
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.629videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.639videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.608videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
A particle of mass m is given initial horizontal velocity of magnitude u as shown in the figure. It transfers to the fixed inclined plane without a jump, that is, its trajectory changes sharply from the horizontal line to the inclined line. All the surfaces are smooth and90∘≥θ>0∘. Then the height to which the particle shall rise on the inclined plane (assume the length of the inclined plane to be very large)
 View Solution
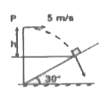
View SolutionA particle of mass m is thrown horizontally from point P , as shown in the figure, with speed 5m/s. It strikes an inclined plane perpendicularly as shown. The inclination of the plane is 30∘ with the horizontal. Then, the height h shown in the figure is ( Take g=10m/s2 ) .
 View Solution
View SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .View Solution
.View SolutionA ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time
 View Solution
View SolutionA ball falls freely form a height onto and smooth inclined plane forming an angle a with the horizontal. Find the ratio of the distance between the points at which the jumping ball strikes the inclined plane. Assume the impacts to be elastic.
View SolutionA particle is projected from the inclined plane at angle 37∘ with the inclined plane in upward direction with speed 10m/s. The angle of inclined plane with horizontal is 53∘. Then the maximum height attained by the particle from the inclined plane will be-
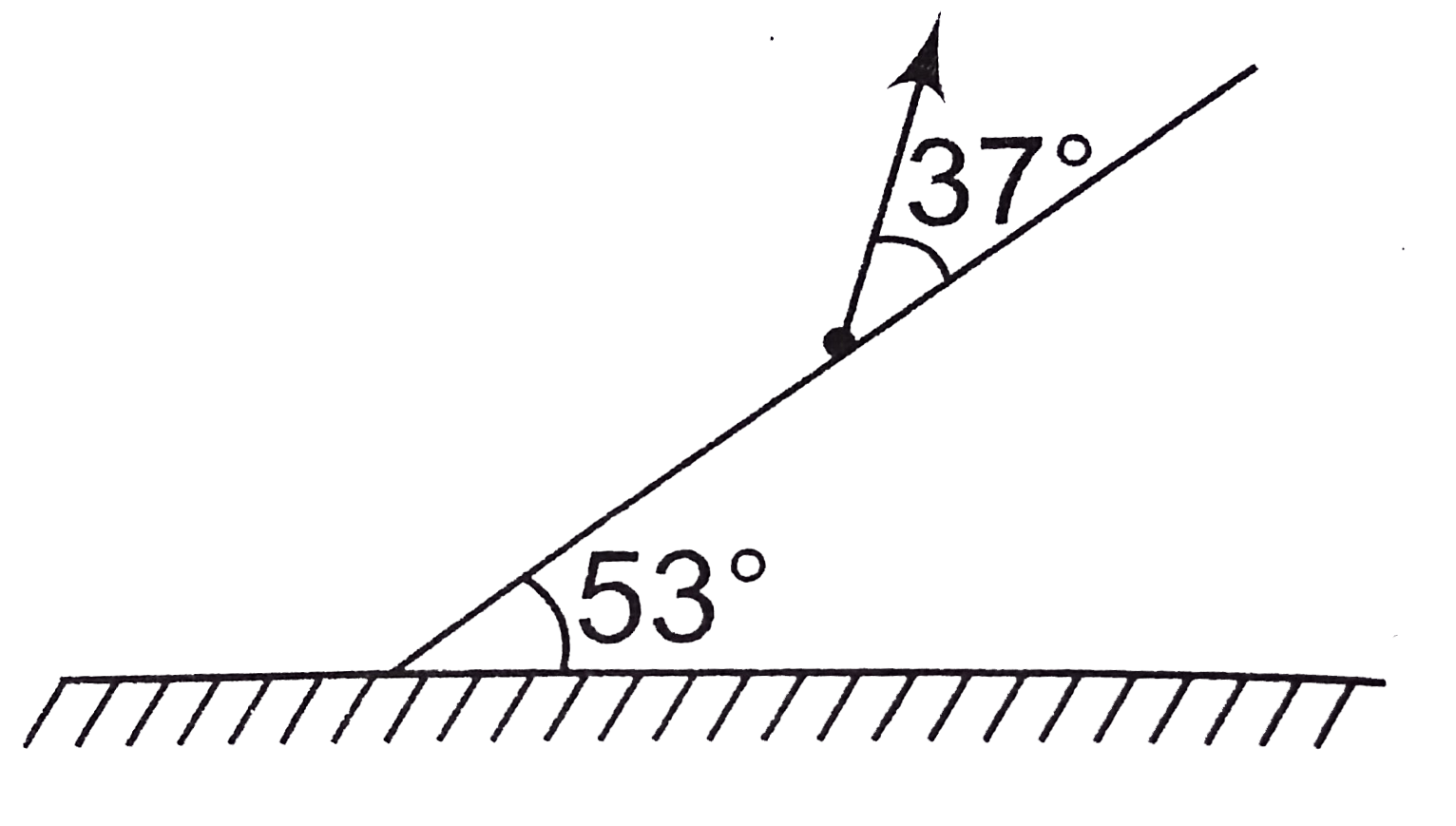 View Solution
View SolutionIn figure, the angle of inclination of the inclined plane is 30∘. Find the horizontal velocity V0 so that the particle hits the inclined plane perpendicularly.
 . View Solution
. View SolutionA block is given velocity 10 m/s along the fixed inclined as shown in figure from the bottom of the inclined plane. Find the total distance travelled along the inclined plane. If the coefficient of friction is equal to 0.5
 View Solution
View SolutionThe horizontal acceleration a that should be given to a smooth inclined plane of angle θ=sin−1(1z) where z > 1, to keep a block stationary relative to the inclined plane as shown in the figure, is
View SolutionA projectile is projected with speed u at an angle of 60∘ with horizontal from the foot of an inclined plane. If the projectile hits the inclined plane horizontally, the range on inclined plane will be.
View Solution


