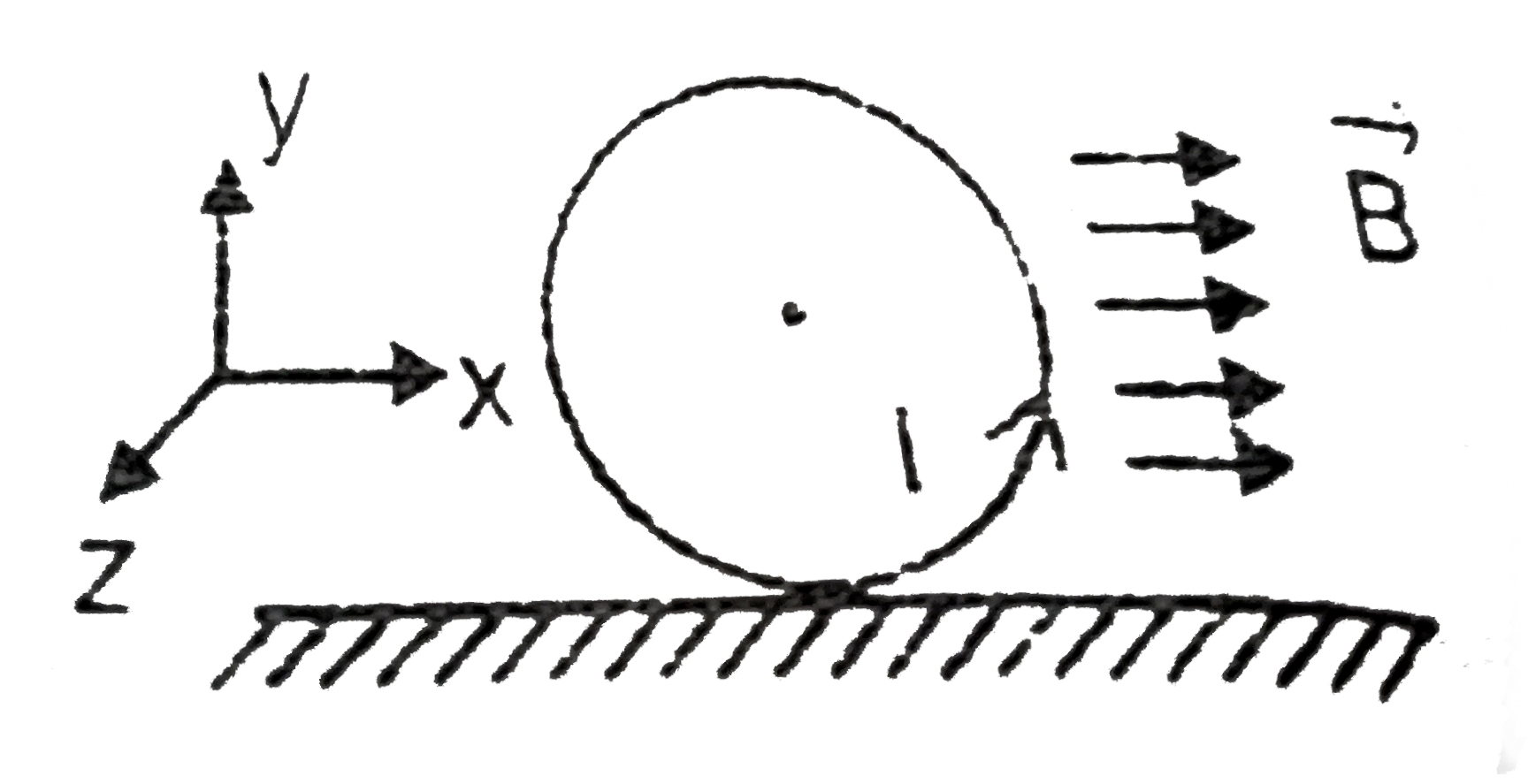
In the shown figure a conducting ring of mass = 2kg and radius R = 0.5 m. lies on a smooth horizontal plane with its plane vertical. The ring carries a current of I=1πA. A horizontal uniform magnetic field of B = 12T is switched on at t =0. The initial angular acceleration α in rad/sec2 of the ring will be 4x if x is :
The correct Answer is:3
τy-axis==Iy-axis⇒(I.πr2)B=1/2mr2α
α=12rad/sec2∴X=3
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.53
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.54
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.51
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A conducting ring of mass 2kg and radius 0.5m is placed on a smooth plane. The ring carries a current of i=4A. A horizontal magnetic field B=10T is switched on at time t=0 as shown in fig The initial angular acceleration of the ring will be
 .
.
View SolutionA conducting ring of mass 2kg and radius 0.5m is placed on a smooth plane. The ring carries a current of i=4A. A horizontal magnetic field B=10T is switched on at time t=0 as shown in fig The initial angular acceleration of the ring will be
 .
.
View SolutionA conducting circular loop of radius a and resistance R is kept on a horizontal plane. A vertical time varying magnetic field B=2t is switched on at time t=0. Then
View SolutionA conducting ring of mass 2kg, radius 0.5m carries a current of 4A. It is placed on a smooth horizontal surface. When a horizontal magnetic field of 10 T parallel to the diameter of the ring is applied, the initial acceleration is (in rad/sec2)

View SolutionA non - conducting ring of mass m = 4 kg and radius R = 10 cm has charge Q = 2 C uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that the plane of the ring is parallel to the surface. A vertical magnetic field B=4t3T is switched on at t = 0. At t = 5 s ring starts to rotate about the vertical axis through the centre. The coefficient of friction between the ring and the surface is found to be k24. Then the value of k is
View SolutionA uniformly conducting wire is bent to form a ring of mass 'm' and radius 'r', and the ring is placed on a rough horizontal surface with its plane horizontal. There exists a uniform and constant horizontal magnetic field of induction B. Now a charge q is passed through the ring in a very small time interval Δt. As a result the ring ultimately just becomes vertical. Calculate the value of g(acceleration due to gravity) in terms of other given quantities. Assume that friction is sufficient to prevent slipping and ignore any loss in energy.
View SolutionA non-conducting ring of mass m and radius R has a charge Q uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that plane of the ring is parallel to the surface. A vertical magnetic field B=B0t2 tesla is switched on. After 2 a from switching on the magnetic field the ring is just about to rotate about vertical axis through its centre.
(a) Find friction coefficient μ between the ring and the surface.
(b) If magnetic field is switched off after 4s, then find the angle rotated by the ring before coming to stop after switching off the magnetic field.
View SolutionA ring of radius R is rolling on a horizontal plane with constant velocity v. There is a constant and uniform magnetic field B which is perpendicular to the plane of the ring. Emf across the lowest point A and right-most point C as shown in the figure will

View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
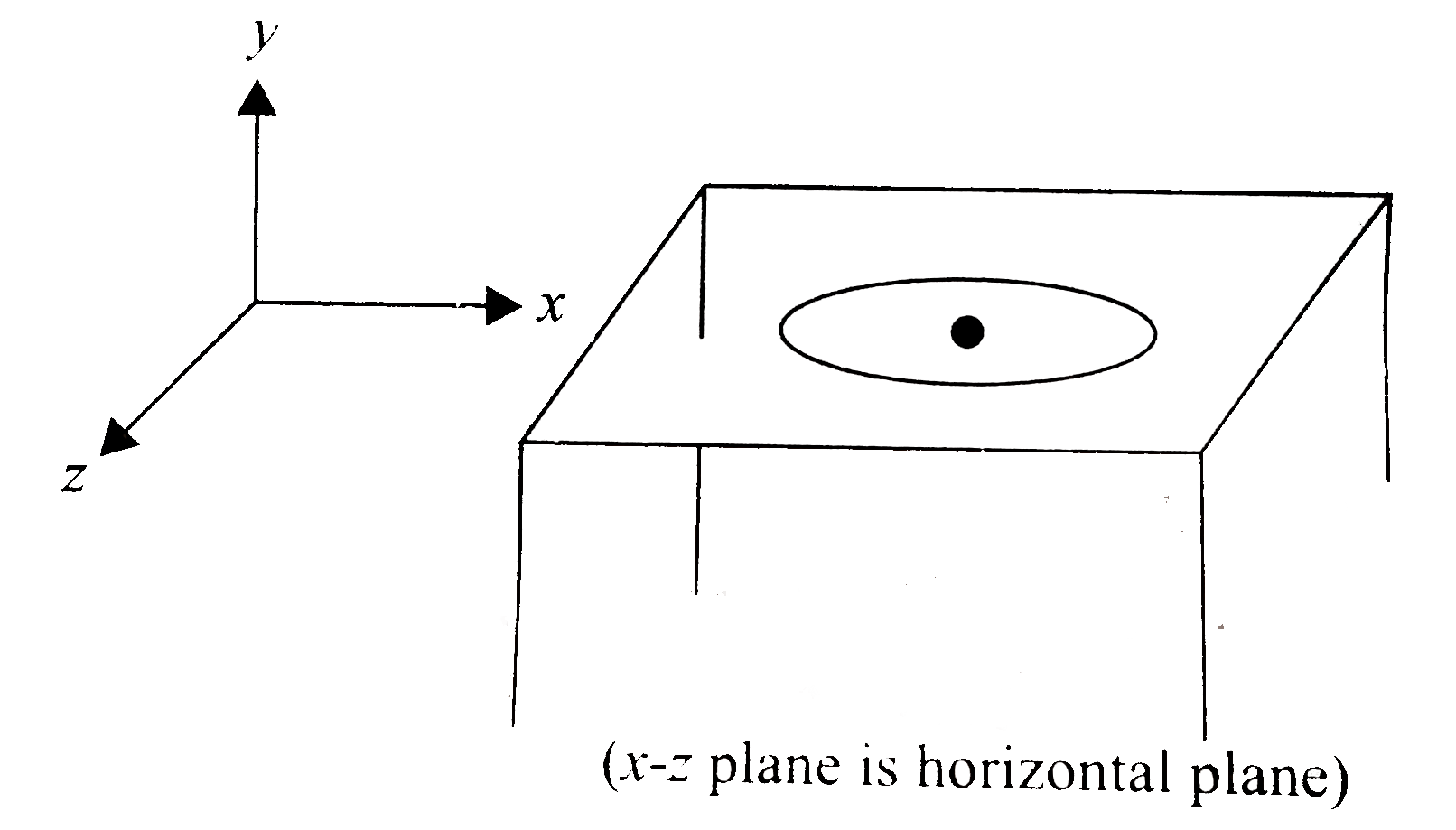
Heat generated (in kJ) through the ring till the instant when ring start toppling is
View SolutionA ring of mass 'm' and radius 'r' carrying current i0 is lying in the X-Y plane with centre at origin. A uniform magnetic field of strength B=B0(2ˆi−3ˆj+5ˆk)T is applied in the region. If the ring rotates about the axid initial magnetic energy stored in the ring will be. (In joules)
View Solution
