The points 'A' and 'B' of a disc are pulled with velocity 'V' as shown in the diagram. Then the velocity of centre 'C' of disc (here the points A, B, C lie on same diameter) will be
 .
.
0
V2
V3
2V3
The correct Answer is:C
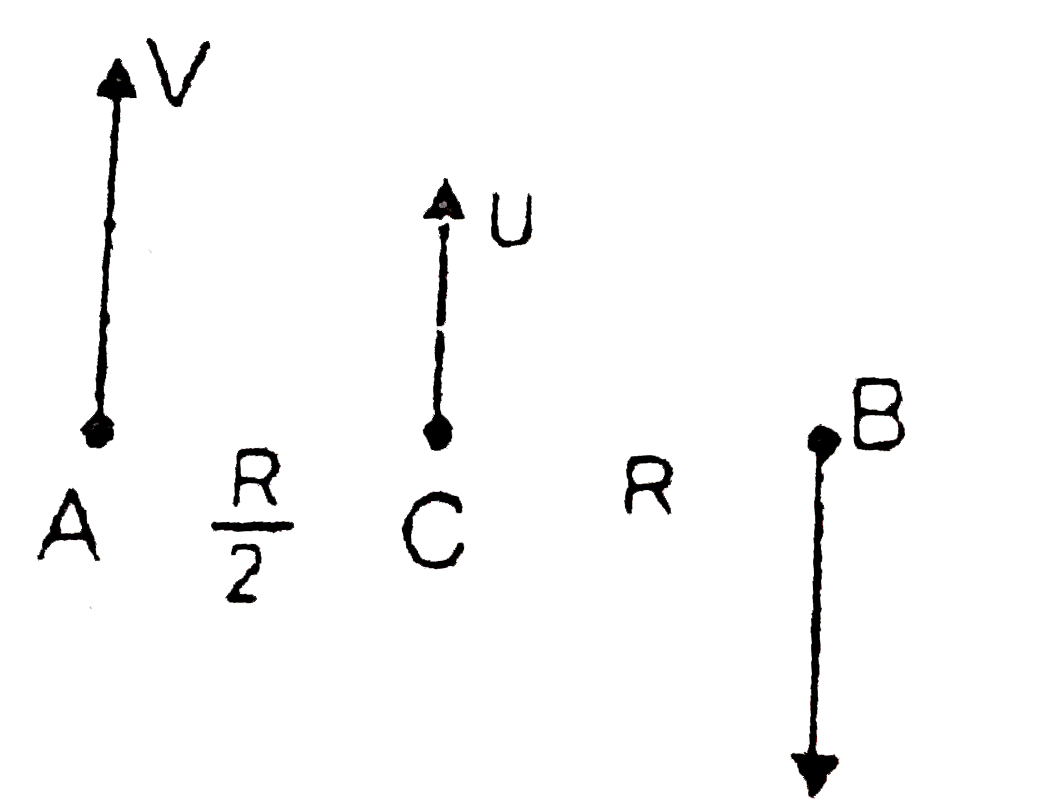
Angular velocity A and B are same with respect to centre C i.e.
V−u(R2)=V+uR⇒u=V3
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.22
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.23
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.20
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions

Due to slipping points A and B on the rim of the disk have the velocities shown. Determine the velocities of the centre point C and point F at this instant.
View Solution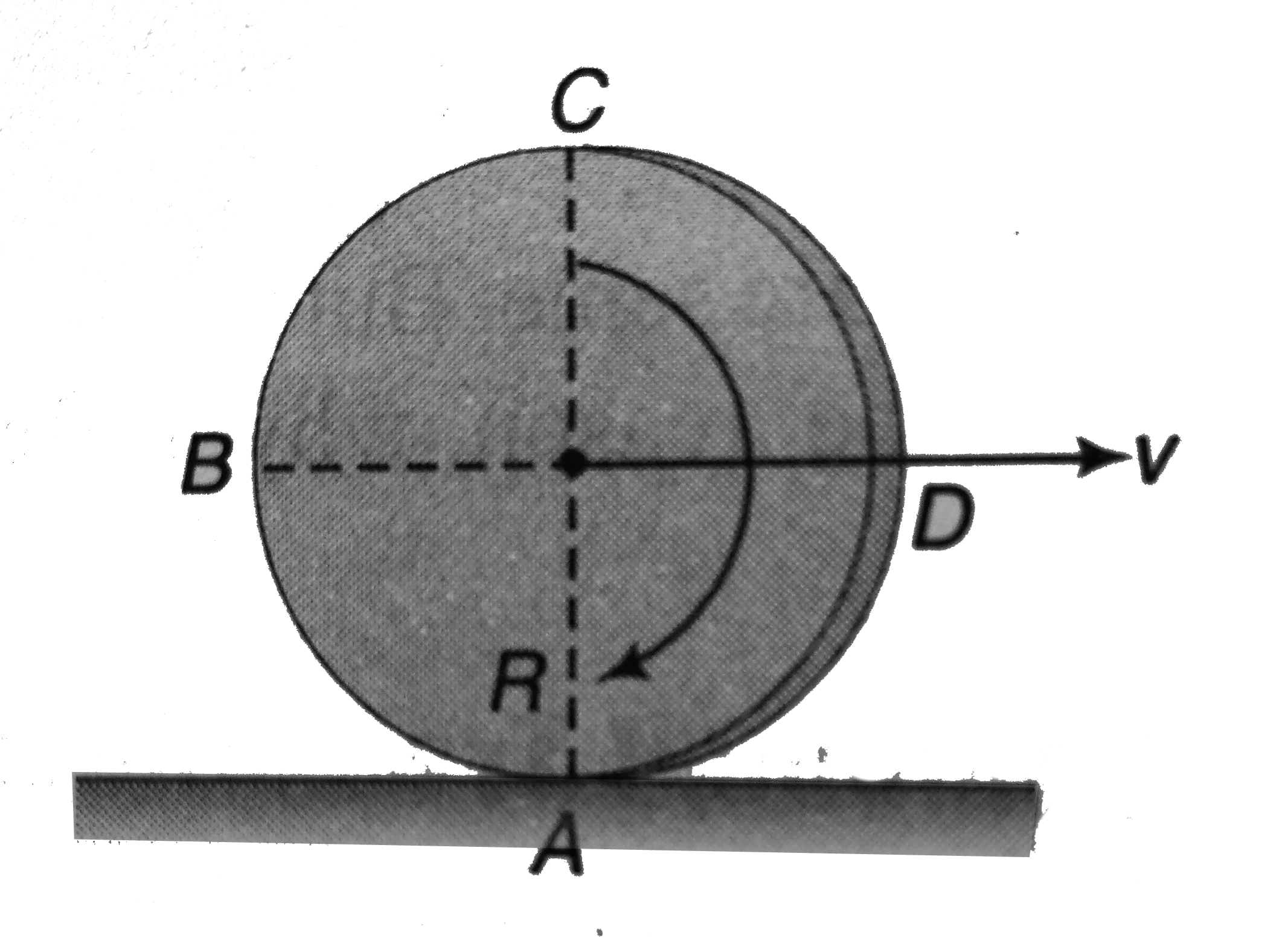
A disc of radius R has linear velocity v and angular velocity ω as shown in the figure. Given υ=rω find velocity of point A, B, C and D on the disc.
View SolutionA disc of mass m and radius R is rolling without slipping as shown in the figure. The magnitude of net velocity of the point P is (OP=R2)
View SolutionA disc is rolling the velocity of its centre of mass is Vcm then which one will be correct : -
View SolutionA disc is rolling on an inclined plane without slipping. The velocity of centre of mass is V. These other point on the disc lie on a circular are having same speed as centre of mass.
When a disc is rolling on an inclined plane. The magnitude of velocities of all the point from the contact point is same, having distance equal to radius r.
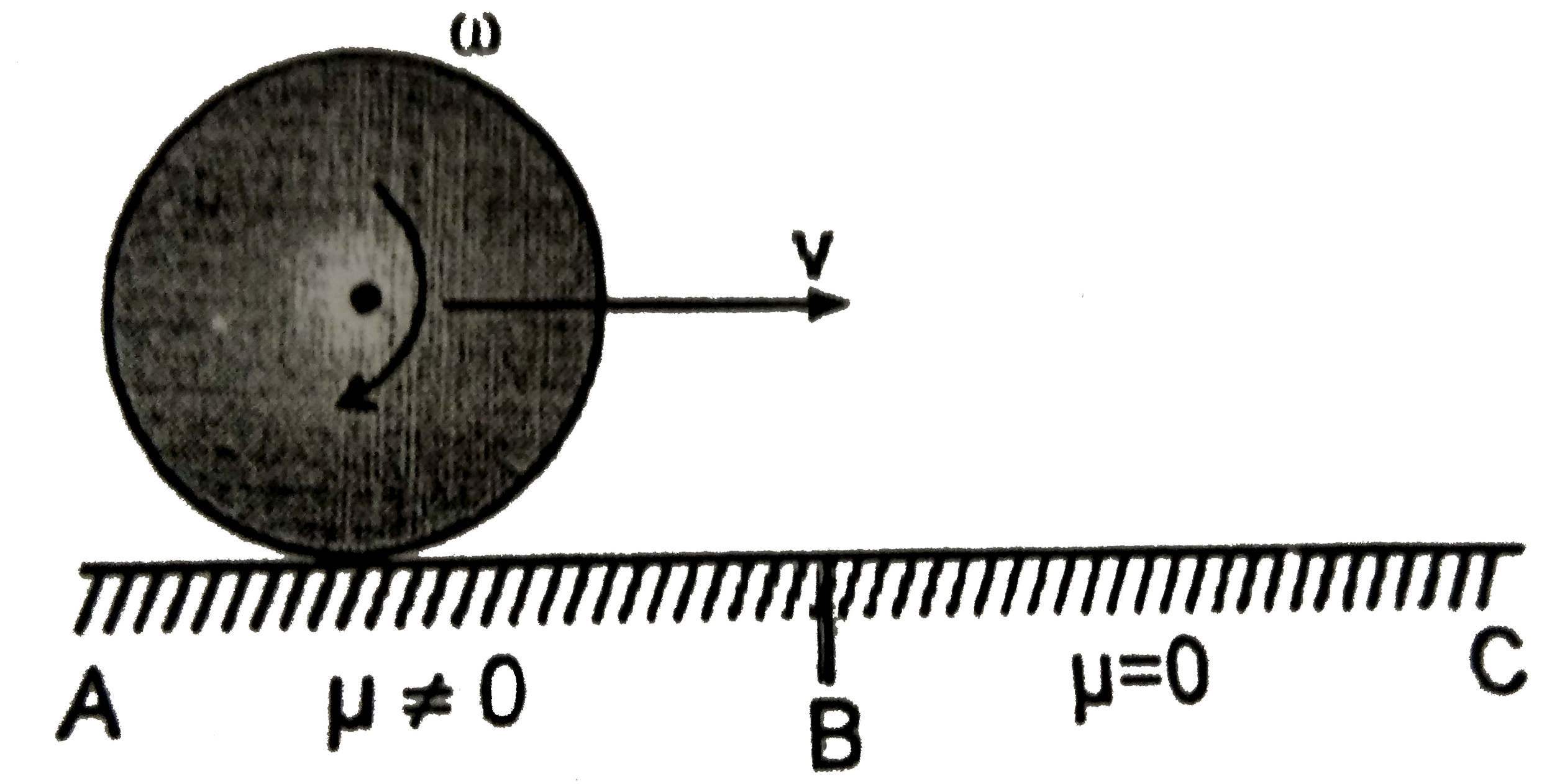
View SolutionAs shown in the figure, a disc of mass m is rolling without slipping a angular velocity ω. When it crosses point B disc will be in :
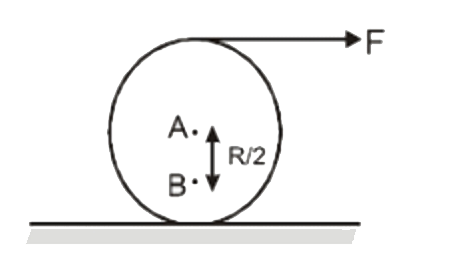
View SolutionA disc of mass m and radius R, is placed on a smooth text service fixed surface . Point A is the geometrical centre of the disc while point B is the centre of mass of the disc . The moment of inertia of the dics about an axis through its centre of mass and perpendicular to the plane of the figure is I .A constant force F is applied to the top of the disc . The acceleration of the centre A of the disc at the instant B is below A (on the same vertical line ) will be :
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionThre identical masses are kept at the corners of an equilateral triangle ABC. A moves towards B with a velocity V, B moves towards C with velocity V, and C moves towards A with same velocity V. Then the velocity of centre of mass of the system of particles is
View SolutionIn the circuit diagram shown in Figure , the potentials of the points B, C and D are respectively -
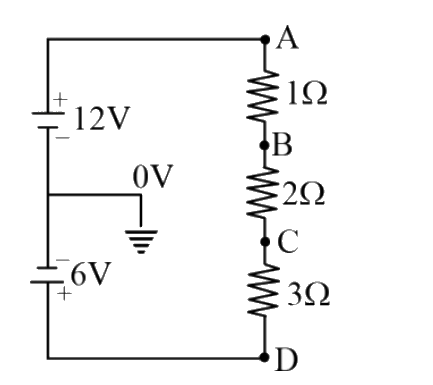
View Solution

