A disc is rolling on an inclined plane without slipping. The velocity of centre of mass is . These other point on the disc lie on a circular are having same speed as centre of mass.
When a disc is rolling on an inclined plane. The magnitude of velocities of all the point from the contact point is same, having distance equal to radius .
Statement I is True, Statement II is True, Statement ll is a correct explanation for Statement I.
Statement I is True, Statement II is True, Statement II is NOT a correct explanation for Statement I
Statement I is True, Statement II is False.
Statement I is False, Statement II is True.
The correct Answer is:A
To solve the problem of a disc rolling on an inclined plane without slipping, we can break it down into the following steps:
Step 1: Understand the Motion of the Disc
When a disc rolls without slipping, the point of contact with the inclined plane has a velocity of zero. This is because it is momentarily at rest relative to the surface it is in contact with.
Hint: Remember that in rolling motion, the point of contact does not move relative to the surface.
Step 2: Identify the Velocity of the Centre of Mass
Let the velocity of the centre of mass of the disc be denoted as V. This is the linear velocity of the disc as it rolls down the incline.
Hint: The centre of mass is the average position of all the mass in the disc, and it moves with velocity V.
Step 3: Relate the Linear Velocity to Angular Velocity
For a disc rolling without slipping, the relationship between the linear velocity V of the centre of mass and the angular velocity ω is given by:
V=r⋅ω
where r is the radius of the disc.
Hint: This relationship is crucial in rolling motion; it connects linear and angular velocities.
Step 4: Analyze Other Points on the Disc
Consider a point P on the disc that is a distance r from the point of contact A. The velocity of point P can be expressed as:
VP=r⋅ω
Since the disc is rolling without slipping, the velocity of point P will also be equal to V.
Hint: All points on the disc that are at a distance r from the point of contact will have the same speed as the centre of mass.
Step 5: Conclusion
Since all points on the disc that are a distance r from the contact point have the same speed as the centre of mass, we can conclude that the statement in the question is true.
Hint: This conclusion reinforces the concept of rolling without slipping, where the velocities of points on the rolling object are consistent with the motion of the centre of mass.
Final Answer
The statement is true: the magnitude of velocities of all points from the contact point is the same, having a distance equal to the radius r.
When a disc rolls without slipping, the point of contact with the inclined plane has a velocity of zero. This is because it is momentarily at rest relative to the surface it is in contact with.
Let the velocity of the centre of mass of the disc be denoted as V. This is the linear velocity of the disc as it rolls down the incline.
For a disc rolling without slipping, the relationship between the linear velocity V of the centre of mass and the angular velocity ω is given by:
V=r⋅ω
where r is the radius of the disc.
Consider a point P on the disc that is a distance r from the point of contact A. The velocity of point P can be expressed as:
VP=r⋅ω
Since the disc is rolling without slipping, the velocity of point P will also be equal to V.
Since all points on the disc that are a distance r from the contact point have the same speed as the centre of mass, we can conclude that the statement in the question is true.
The statement is true: the magnitude of velocities of all points from the contact point is the same, having a distance equal to the radius r.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Linked Comprehension
Explore 71 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Integer
Explore 7 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Single Correct
Explore 142 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
Knowledge Check
A solid cylinder of mass M and radius R rolls down an inclined plane without slipping. THE speed of its centre of mass when it reaches the bottom is
A√(2gh)B√4/3.ghC√3/4.ghD√(4g/h)
A disc of radius R is rolling down an inclined plane whose angle of inclination is θ Its acceleration would be
View SolutionA disc rolls on ground without slipping . Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ . Suppose vp is the speed of this point. Then, match the following the following table.

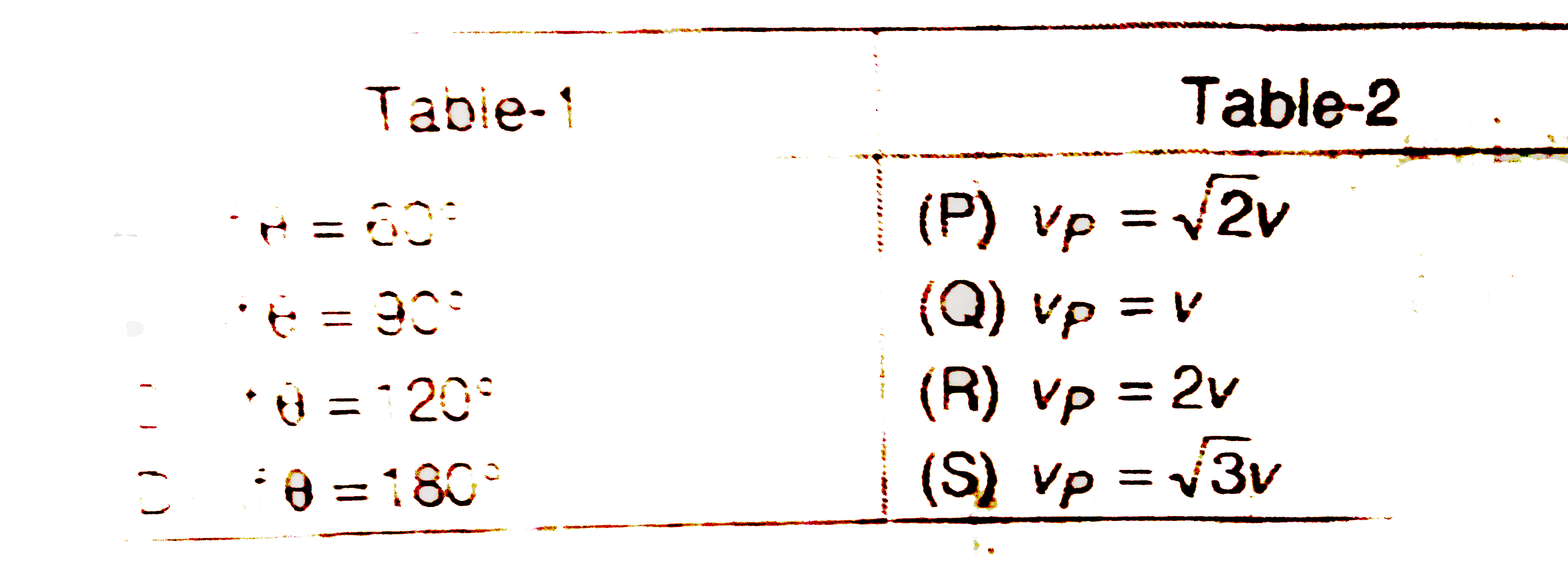
View SolutionA disc rolls down a plane of length L and inclined at angle θ, without slipping. Its velocity on reaching the bottom will be :-
View SolutionA disc and a solid sphere of same mass and radius roll down an inclined plane. The ratio of thhe friction force acting on the disc and sphere is
View SolutionThe acceleration of the centre of mass of uniform solid disc rolling down an inclined plane of angle α is xgsinα. Find x
View SolutionIf a ring, a disc, a solid sphere and a cyclinder of same radius roll down an inclined plane, the first one to reach the bottom will be:
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
View Solution