A metal coin at the bottom of a beaker filled with a liquid of refractive index 4/3 to height of 6cm. To an observer looking from above the surface of the liquid, coin will appear at a depth of (consider paraxial rays).
7.5cm
6.75cm
4.5cm
1.5cm
The correct Answer is:C
To solve the problem of finding the apparent depth of a metal coin submerged in a liquid with a refractive index of 43, we can use the formula for apparent depth in optics. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have a beaker filled with a liquid of height h=6cm and a refractive index μ=43. The observer is looking from above the surface of the liquid. We need to find the apparent depth h′ of the coin.
Step 2: Use the Formula for Apparent Depth
The formula for apparent depth when viewed from a medium of refractive index μ is given by:
h′=hμ
where:
- h′ is the apparent depth,
- h is the real depth,
- μ is the refractive index of the liquid.
Step 3: Substitute the Values
Substituting the values into the formula:
- Real depth h=6cm
- Refractive index μ=43
We get:
h′=6cm43=6cm×34
Step 4: Calculate the Apparent Depth
Now, calculate h′:
h′=6×34=184=4.5cm
Conclusion
Thus, the coin will appear at a depth of 4.5cm.
Final Answer
The apparent depth of the coin is 4.5cm.
---
We have a beaker filled with a liquid of height h=6cm and a refractive index μ=43. The observer is looking from above the surface of the liquid. We need to find the apparent depth h′ of the coin.
The formula for apparent depth when viewed from a medium of refractive index μ is given by:
h′=hμ
where:
- h′ is the apparent depth,
- h is the real depth,
- μ is the refractive index of the liquid.
Substituting the values into the formula:
- Real depth h=6cm
- Refractive index μ=43
h′=6cm43=6cm×34
Now, calculate h′:
h′=6×34=184=4.5cm
Thus, the coin will appear at a depth of 4.5cm.
The apparent depth of the coin is 4.5cm.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.8
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.9
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.6
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels up to the surface of the liquid and moves along its surface (see figure ).
How fast is the light travelling in the liquid ?

View SolutionA point source of light S is placed at the bottom of a vessel containg a liquid of refractive index 5/3. A person is viewing the source from above the surface. There is an opaque disc of radius 1cm floating on the surface. The centre of the disc lies vertically above the source S. The liquid from the vessel is gradually drained out through a tap. What is the maximum height of the liquid for which the source cannot at all be seen from above?
View Solution
Knowledge Check
The apparent depth of a needle laying at the bottom of the tank, which is filled with water of refractive index 1.33 to a height of 12.5 cm is measured by a microscope to be 9.4cm. If water is replaced by a liquid of refractive index 1.63 upto the same height. What distance would the microscope have to be moved to focus on the needle again ?
A1.73cmB2.13cmC1.5cmD2.9cm
A coin is placed at the bottom of a beaker containing water (refractive index=4/3) at a depth of 12cm. By what height the coin appears to be raised when seen from vertical above ?
View SolutionA vesserl contains a slab of glass 8cm thick and of refractive index 1.6 . Over the slab, the vessel is filled by oil of refractive index μ upto height 4.5 cm and then by another liquid, i.e., water of refractive index 4/3 and height 6cm as shown in Figure. An observer looking down from above observer that a mark at the bottom of glass slab appears to be raised up to a position 6cm from bottom of the slab. Find refractive index of oil (μ) .

View SolutionA small illuminated bulb is at the bottom of a tank, containing a liquid of refractive index μ upto a height H. Find the expression for the diameter of an opaque disc, floating symmetrically on the liquid surface in order to cut- off the light from the bulb.
View SolutionA man is standing at the edge of a 1m deep swimming pool, completely filled with a liquid of refractive index √32. The eyes of the man are √3m above the ground. A coin located at the bottom of the pool appears to be an angle of depression of 30∘ with reference to the eyes of man. Then horizontal distance (represented by x in the figure) of the coin from the eye of the man is ...........mm.
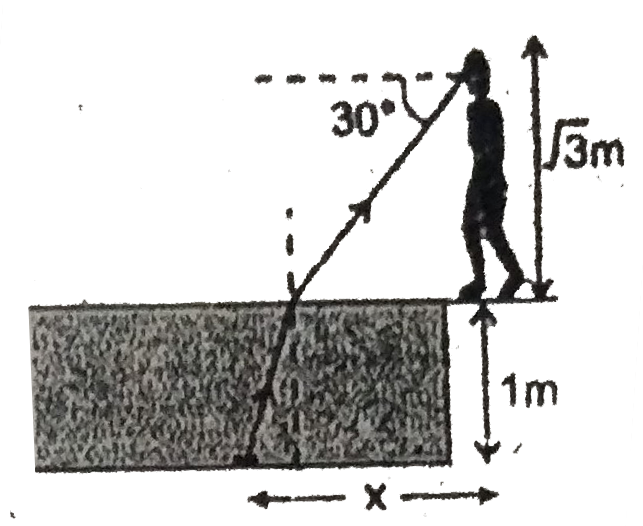
View SolutionA man is standing at the edge of a 1m deep swimming pool, completely filled with a liquid of refractive index √32. The eyes of the man are √3m above the ground. A coin located at the bottom of the pool appears to be an angle of depression of 30∘ with reference to the eyes of man. Then horizontal distance (represented by x in the figure) of the coin from the eye of the man is ...........mm.

View SolutionA coin placed at the bottom of a beaker appears to be raised by 4.0 cm. If the refractive index of water is 4/3, find the depth of the water in the beaker.
View SolutionA vessel of depth 2h is half filled with a liquid of refractive index 2√2 and the upper half with another liquid of refractive index √2. The liquids are immiscible. The apparent depth of the inner surface of the bottom of vessel will be:
View Solution
