A coin placed at the bottom of a beaker appears to be raised by 4.0 cm. If the refractive index of water is 4/3, find the depth of the water in the beaker.
To solve the problem, we need to find the depth of water in the beaker using the given information about the apparent rise of the coin and the refractive index of water.
1. Understanding the Refractive Index:
The refractive index (μ) of a medium is defined as the ratio of the real depth (actual depth) to the apparent depth (depth perceived by an observer). The formula is given by:
μ=Real DepthApparent Depth
2. Identifying Variables:
- Let the real depth of the water in the beaker be x cm.
- The apparent depth of the coin, which appears to be raised by 4 cm, is given by:
Apparent Depth=x−4 cm
3. Substituting Values into the Formula:
Given that the refractive index of water is 43, we can substitute the values into the refractive index formula:
43=xx−4
4. Cross-Multiplying to Solve for x:
To eliminate the fraction, we cross-multiply:
4(x−4)=3x
Expanding this gives:
4x−16=3x
5. Rearranging the Equation:
Now, we can rearrange the equation to isolate x:
4x−3x=16
Simplifying this results in:
x=16 cm
6. Conclusion:
The depth of the water in the beaker is 16 cm.
Final Answer:
The depth of the water in the beaker is 16 cm.
The refractive index (μ) of a medium is defined as the ratio of the real depth (actual depth) to the apparent depth (depth perceived by an observer). The formula is given by:
μ=Real DepthApparent Depth
- Let the real depth of the water in the beaker be x cm.
- The apparent depth of the coin, which appears to be raised by 4 cm, is given by:
Apparent Depth=x−4 cm
Given that the refractive index of water is 43, we can substitute the values into the refractive index formula:
43=xx−4
To eliminate the fraction, we cross-multiply:
4(x−4)=3x
Expanding this gives:
4x−16=3x
Now, we can rearrange the equation to isolate x:
4x−3x=16
Simplifying this results in:
x=16 cm
The depth of the water in the beaker is 16 cm.
The depth of the water in the beaker is 16 cm.
Topper's Solved these Questions
Similar Questions
A pond appears to be 2.7 m deep. If the refractive index of water is 43, find the actual depth of the pond.
View SolutionThe refractive index of water is 4/3. The speed of light in water is
View SolutionA water pond appears to be 2⋅7m dep. If the refractive index of water is 4/3, find the actual depth of the pond.
View SolutionThe refractive index of water is 4/3'. Explain the meaning of this statement.
View SolutionBrewster angle for air to water transition is (refractive index of water is 43)
View SolutionWhy is a coin placed in a bowl of water appears raised?
View SolutionA mark at the bottom of a liquid appears to rise by 0.1m. The depth of the liquid is 1m. The refractive index of the liquid is
View SolutionA coin is placed at the bottom of a beaker containing water (refractive index=4/3) at a depth of 12cm. By what height the coin appears to be raised when seen from vertical above ?
View SolutionA man observes a coin placed at the bottom of a beaker which contains two immiscible liquids of refractive indices 1.2 and 1.4 as shown in the figure. Find the depth of the coin below the surface, as observed from above.
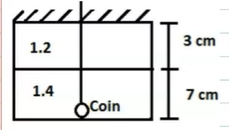
View SolutionAssertion A diverging lens (in air) cannot be made more diverging whatever be the medium we choose completely immerse the lens.
Reason The minimum refractive index of any medium is 1.
View Solution

