A small illuminated bulb is at the bottom of a tank, containing a liquid of refractive index μ upto a height H. Find the expression for the diameter of an opaque disc, floating symmetrically on the liquid surface in order to cut- off the light from the bulb.
To find the expression for the diameter of an opaque disc floating symmetrically on the surface of a liquid in a tank containing a bulb at the bottom, we can follow these steps:
1. Understand the Setup:
- We have a small illuminated bulb at the bottom of a tank filled with a liquid of refractive index μ up to a height H.
- We need to find the diameter of an opaque disc that floats on the surface of the liquid and cuts off the light from the bulb.
2. Identify the Critical Angle:
- Light emitted from the bulb travels through the liquid and can undergo total internal reflection (TIR) at the surface.
- The critical angle c for TIR can be defined using Snell's law:
sinc=1μ
3. Calculate Cosine of the Critical Angle:
- Using the identity cosc=√1−sin2c:
cosc=√1−(1μ)2=√μ2−1μ2
4. Establish the Relationship Between Angles:
- When light reaches the surface at point P, the angle of incidence is equal to the critical angle c. The tangent of the critical angle can be expressed as:
tanc=oppositeadjacent=RH
- Here, R is the radius of the disc and H is the height of the liquid.
5. Set Up the Equation:
- From the previous steps, we have two expressions for tanc:
tanc=1√μ2−1(from TIR)
tanc=RH(from triangle)
- Setting these equal gives:
RH=1√μ2−1
6. Solve for the Radius R:
- Rearranging the equation:
R=H√μ2−1
7. Calculate the Diameter:
- The diameter D of the disc is twice the radius:
D=2R=2×H√μ2−1=2H√μ2−1
Final Expression:
The expression for the diameter of the opaque disc is:
D=2H√μ2−1
- We have a small illuminated bulb at the bottom of a tank filled with a liquid of refractive index μ up to a height H.
- We need to find the diameter of an opaque disc that floats on the surface of the liquid and cuts off the light from the bulb.
- Light emitted from the bulb travels through the liquid and can undergo total internal reflection (TIR) at the surface.
- The critical angle c for TIR can be defined using Snell's law:
sinc=1μ
- Using the identity cosc=√1−sin2c:
cosc=√1−(1μ)2=√μ2−1μ2
- When light reaches the surface at point P, the angle of incidence is equal to the critical angle c. The tangent of the critical angle can be expressed as:
tanc=oppositeadjacent=RH
- Here, R is the radius of the disc and H is the height of the liquid.
- From the previous steps, we have two expressions for tanc:
tanc=1√μ2−1(from TIR)
tanc=RH(from triangle)
- Setting these equal gives:
RH=1√μ2−1
- Rearranging the equation:
R=H√μ2−1
- The diameter D of the disc is twice the radius:
D=2R=2×H√μ2−1=2H√μ2−1
The expression for the diameter of the opaque disc is:
D=2H√μ2−1
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION-C50videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - PHYSICS (Theory) DELHI BOARD -2016 [SET -I][COMPTT.]11videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION-A28videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
A point source of light S is placed at the bottom of a vessel containg a liquid of refractive index 5/3. A person is viewing the source from above the surface. There is an opaque disc of radius 1cm floating on the surface. The centre of the disc lies vertically above the source S. The liquid from the vessel is gradually drained out through a tap. What is the maximum height of the liquid for which the source cannot at all be seen from above?
View SolutionA concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
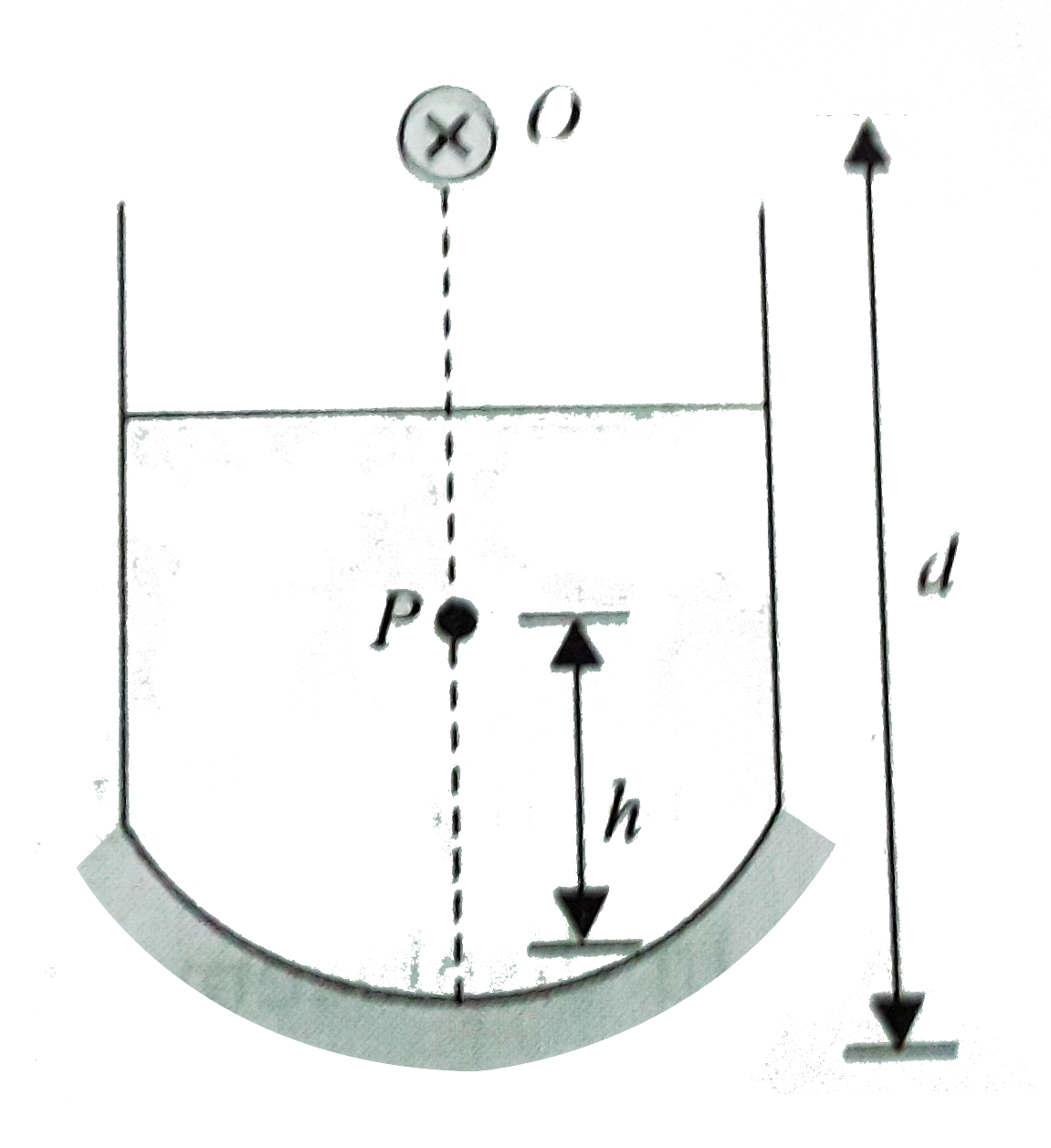 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A small bulb (assumed to be a point source) is placed at the bottom of a tank containing water to a depth of 80cm. Find out the area of the surface of water through which light from the bulb can emerge. Take the value of refractive index of water to be 4/3.
A2.6m2B3.6m2C4.2m2D5.8m2 - Question 2 - Select One
The apparent depth of a needle laying at the bottom of the tank, which is filled with water of refractive index 1.33 to a height of 12.5 cm is measured by a microscope to be 9.4cm. If water is replaced by a liquid of refractive index 1.63 upto the same height. What distance would the microscope have to be moved to focus on the needle again ?
A1.73cmB2.13cmC1.5cmD2.9cm
A plane mirror is placed at the bottom of a tank containing a liquid of refractive index μ. P is a small object at a height h above the mirror. An observer observes P and its image in the mirror. The apparent distance between two will be
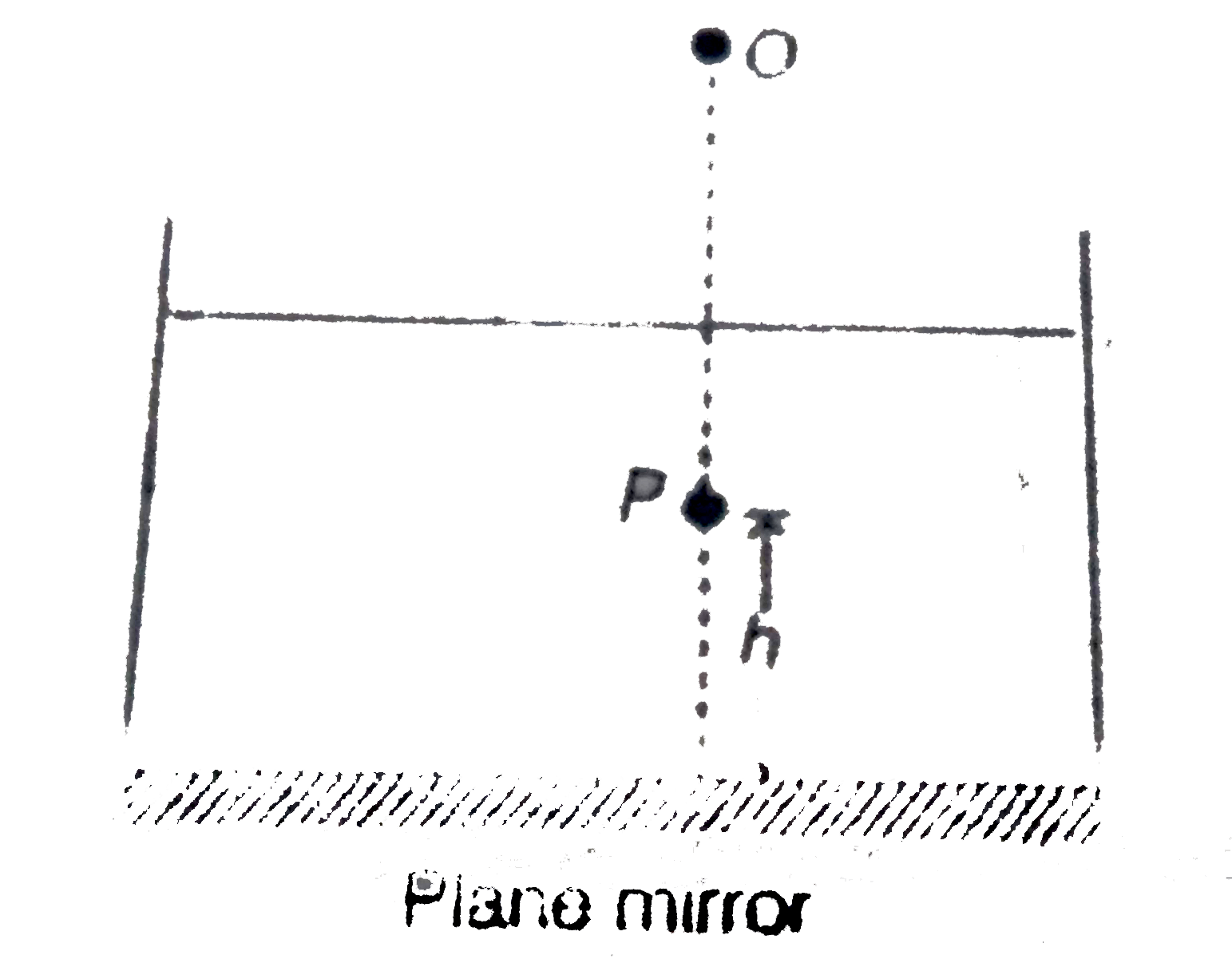 View Solution
View SolutionA metal coin at the bottom of a beaker filled with a liquid of refractive index 4/3 to height of 6cm. To an observer looking from above the surface of the liquid, coin will appear at a depth of (consider paraxial rays).
View SolutionA man observes a coin placed at the bottom of a beaker which contains two immiscible liquids of refractive indices 1.2 and 1.4 as shown in the figure. Find the depth of the coin below the surface, as observed from above.
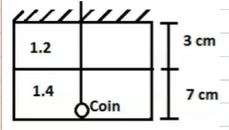 View Solution
View SolutionThere is a small hole in the bottom of a fixed container containing a liquid upto height 'h'. The top of the liquid as well as the hole at the bottom are exposed to atmosphere. As the liquid come out of the hole. (Area of the hole is 'a' and that of the top surface is 'A') :
View SolutionA small bulb (assumed to be a point source) is placed at the bottom of a tank containing water to a depth of 80cm. Find out the area of the surface of water through which light from the bulb can emerge. Take the value of refractive index of water to be 4/3.
View SolutionConsider a tank made of glass (refractive index 1.5) with a thick bottom. It is filled with a liquid of refractive index μ. A student finds that, irrespective of what the incident angle I (see figure) is for a beam of light entering the liquid, the light reflected from the liquid glass interface is never completely polarized. For this to happen, the minimum value of μ is :
 View Solution
View Solution

