An object is moving in a circle at constant speed . The magnitude of rate of change of momentum of the object.
is zero
is proportional to
is proportional to
is proportional to
The correct Answer is:C
To solve the problem of finding the magnitude of the rate of change of momentum of an object moving in a circle at constant speed v, we can follow these steps:
Step 1: Understand the motion
The object is moving in a circular path with a constant speed v. Although the speed is constant, the direction of the velocity is continuously changing, which means the momentum of the object is also changing.
Step 2: Define momentum
Momentum p is defined as the product of mass m and velocity v:
p=m⋅v
Step 3: Determine the rate of change of momentum
The rate of change of momentum is given by the derivative of momentum with respect to time:
dpdt=d(mv)dt
Since mass m is constant, we can write:
dpdt=mdvdt+vdmdt
However, since mass m is constant, dmdt=0, thus:
dpdt=mdvdt
Step 4: Analyze the velocity change
In circular motion, even though the speed v is constant, the direction of the velocity vector is changing. The change in velocity Δv over a time interval Δt leads to a centripetal acceleration ac given by:
ac=v2r
where r is the radius of the circular path.
Step 5: Relate acceleration to force
The net force acting on the object, which is the centripetal force Fc, is related to the mass and acceleration:
Fc=m⋅ac=m⋅v2r
Step 6: Connect force to rate of change of momentum
According to Newton's second law, the force is also equal to the rate of change of momentum:
F=dpdt
Thus, we have:
dpdt=m⋅v2r
Conclusion
The magnitude of the rate of change of momentum of the object is:
dpdt=mv2r
The object is moving in a circular path with a constant speed v. Although the speed is constant, the direction of the velocity is continuously changing, which means the momentum of the object is also changing.
Momentum p is defined as the product of mass m and velocity v:
p=m⋅v
The rate of change of momentum is given by the derivative of momentum with respect to time:
dpdt=d(mv)dt
Since mass m is constant, we can write:
dpdt=mdvdt+vdmdt
However, since mass m is constant, dmdt=0, thus:
dpdt=mdvdt
In circular motion, even though the speed v is constant, the direction of the velocity vector is changing. The change in velocity Δv over a time interval Δt leads to a centripetal acceleration ac given by:
ac=v2r
where r is the radius of the circular path.
The net force acting on the object, which is the centripetal force Fc, is related to the mass and acceleration:
Fc=m⋅ac=m⋅v2r
According to Newton's second law, the force is also equal to the rate of change of momentum:
F=dpdt
Thus, we have:
dpdt=m⋅v2r
The magnitude of the rate of change of momentum of the object is:
dpdt=mv2r
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 50
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 51
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 48
4 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Knowledge Check
A particle is moving in a circle with uniform speed. IT has constant
AvelocityBAccelerationCkinetic energyDdisplacement
An object is moving with variable speed, then
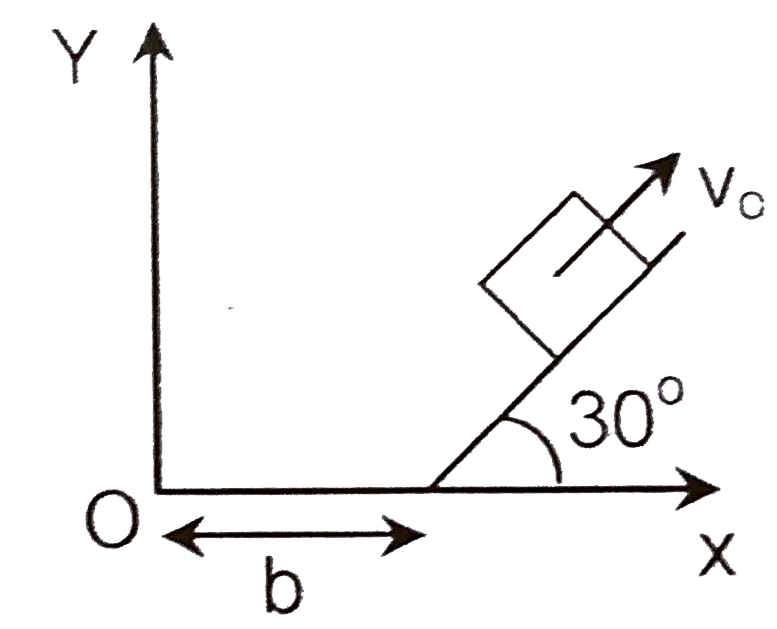
View SolutionA cube of mass m and side a is moving along a plane with constant speed vo as shown in figure. The magnitude of angular momentum of the cube about z -axis would be.
View SolutionA particle is moving along a circular path with a constant speed 10ms−1.What is the magnitude of the change in velocity of the particle ,when it moves through an angle of 60∘ around the center of the circle ?
View SolutionA particle is moving in a circle of radius r having centre at O with a constant speed v . The magnitude of change in velocity in moving from A to B is

View SolutionA force F=(2tˆi+3t2ˆj)N acts on an object moving in XY-plane. Find the magnitude of change in momentum of the object in the time interval t=0 to t=2s.
View SolutionA ball of mass 50 g moving at a speed of 2.0 m/s strikes a plane surface at an angle of incidence 450. The ball is reflected by the plane at equal angle of reflection with the same speed. Calculate a. the magnitude of the change in momentum of the ball b. the change in the magnitude of the momentum of the wall.
View SolutionA woman throws an object of mass 500 g with a speed of 25ms−1 .
(a) What is the impulse imparted to the object ?
(b) If the object hitts a wall and rebounds with the half the original speed , what is the change in momentum of the object ?
View Solution
