Question

A block of mass $m$ rests on a rough horizontal plane having coefficient of kinetic friction ${\mu }_k$ and coefficient of static friction ${\mu }_s$. The spring is in its natural, when a constant force of magnitude $P=\frac{5{\mu }_{k}mg}{4}$ starts acting on the block. The spring force $F$ is a function of extension $x$ as $F=k{x}^2.($ Where $k$ is spring constant $)$

$\left(a\right)$ Comment on the relation between ${\mu }_s$ and ${\mu }_k$ for the motion to start.
$\left(b\right)$ Find the maximum extension in the spring $($ Assume the force $P$ is sufficient make the block move $)$.

Answer

(a) `5mu_(K) > 4mu_(s)`,(b) `x=((mu_(K)mg)/(K))^(1//3)`

Explanation

`(a) ` For motion to start
`(5mu_(k)mg)/(4) gt mu _(s) mg or 5mu_(k)gt 4 mu _(s)`
`(b)` ,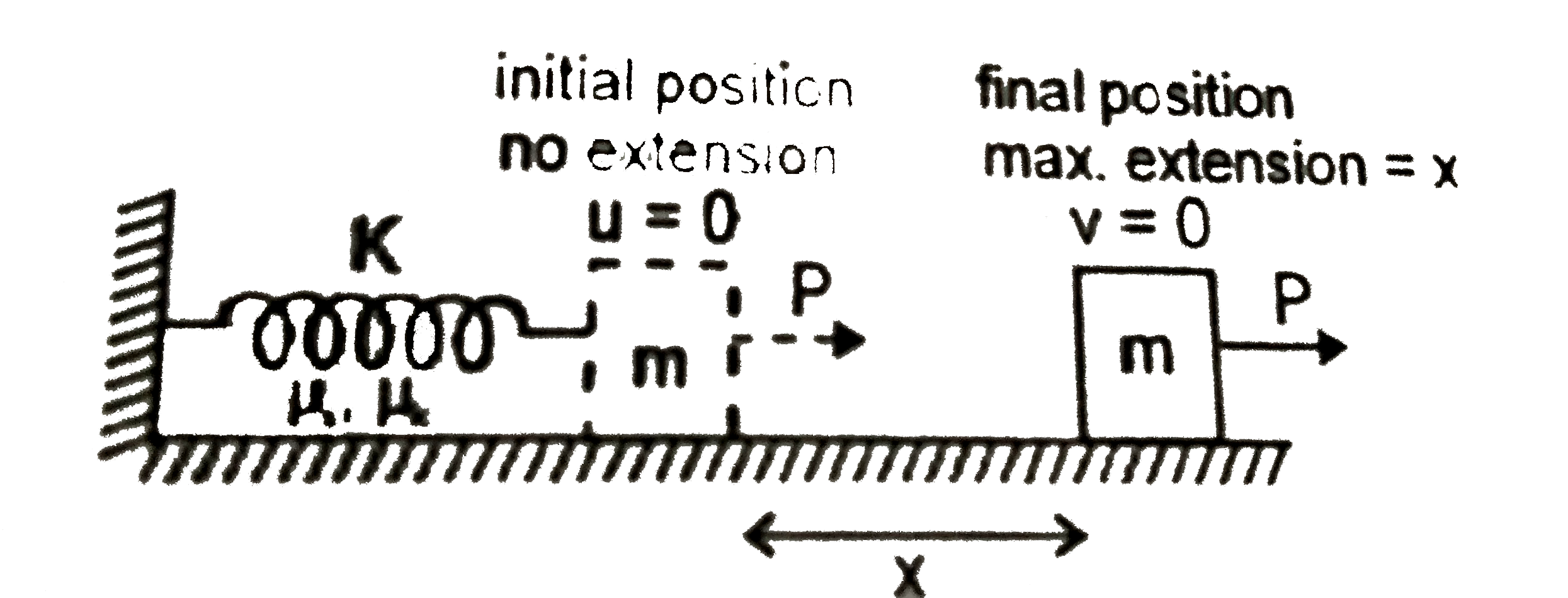
At the final position of block extension in spring is maximum and the sped of the block is `v=0` .Hence the net work done in taking the block from initial to final position.
`Delta W =` work donw by `P+` work donw by spring force `F+` work done by friction `=0`
`=Px-underset(0)overset(x)int Kx^(3).dx-mu mg x=(5mu_(k)mg)/(4)x-(Kx^(4))/(4)-mu_(k)mg x =0`
solving we get `x=((mu_(K)mg)/(K))^(3//2)Ans. `