A particle of mass 0.1kg is launched at an angle of 53∘ with the horizontal . The particle enters a fixed rough hollow tube whose length is slightly less than 12.5m and which is inclined at an angle of 37∘ with the horizontal as shown in figure. It is known that the velocity of ball when it enters the tube is parallel to the axis of the tube. The coefficient of friction betweent the particle and tube inside the tube is μ=38[ Take g=10m/g2]
![A particle of mass 0.1kg is launched at an angle of 53^(@) with the horizontal . The particle enters a fixed rough hollow tube whose length is slightly less than 12.5m and which is inclined at an angle of 37^(@) with the horizontal as shown in figure. It is known that the velocity of ball when it enters the tube is parallel to the axis of the tube. The coefficient of friction betweent the particle and tube inside the tube is mu=(3)/(8)[ Take g=10m//g^(2)] The distance from the point of projection where the particle will land on the horizontal plane after coming out from the tube is approximately equal to :](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_PHY_DPP_41_XI_E01_342_Q01.png)
The distance from the point of projection where the particle will land on the horizontal plane after coming out from the tube is approximately equal to :
8.4m
10m
18.4m
36.8m
The correct Answer is:C
Time taken by projectile to reach the bottom of tube from point of projection is
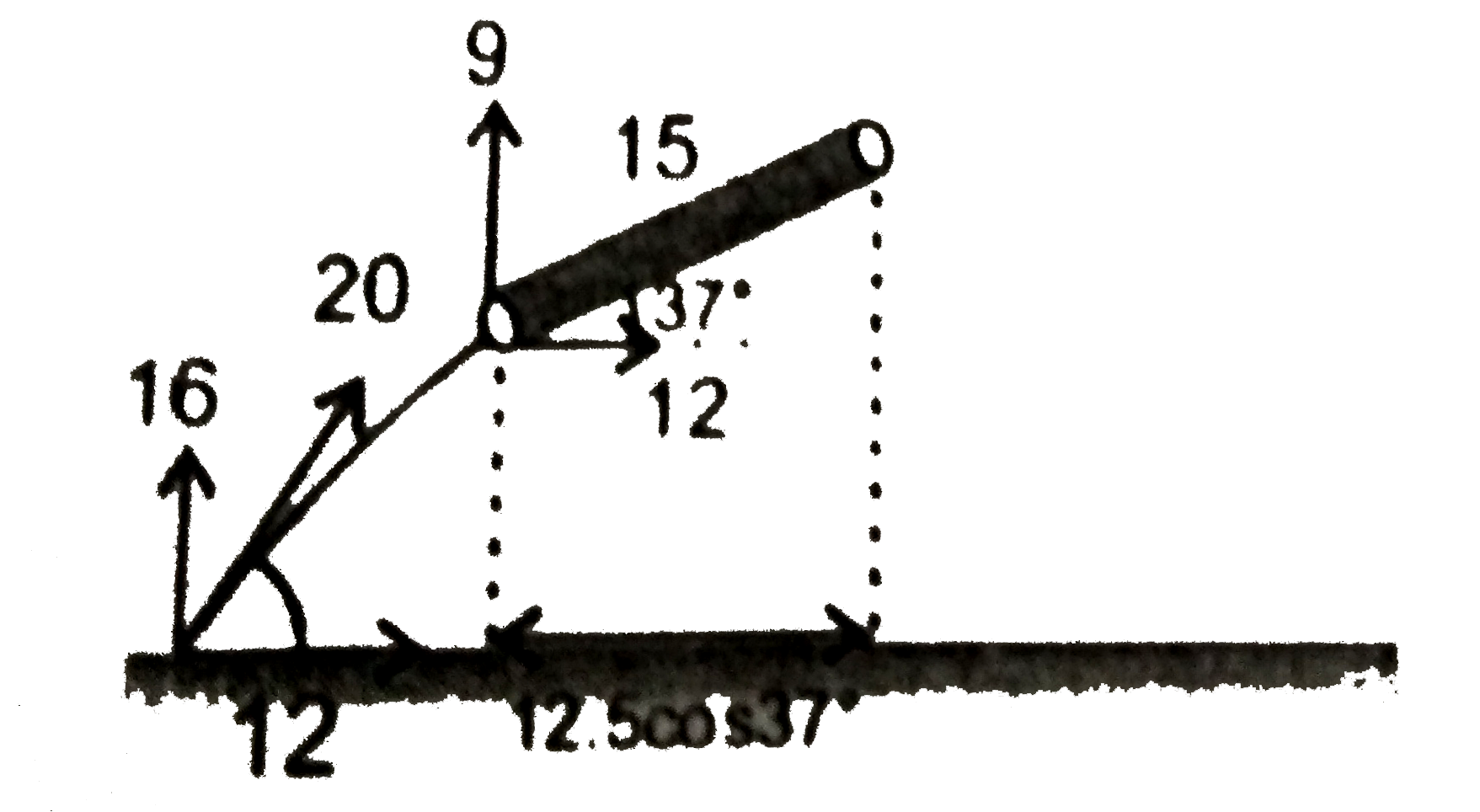
9−16−gt∴T=710=0.7sec.
During this time particle travels 12×0.7m
=8.4m horizontally.
∴ Take distance =8.4m+12.5cos37∘
=.4+10=18.4m.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 707videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 718videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 695videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A particle of mass 0.1kg is launched at an angle of 53∘ with the horizontal . The particle enters a fixed rough hollow tube whose length is slightly less than 12.5m and which is inclined at an angle of 37∘ with the horizontal as shown in figure. It is known that the velocity of ball when it enters the tube is parallel to the axis of the tube. The coefficient of friction betweent the particle and tube inside the tube is μ=38[ Take g=10m/g2]

The velocity of the particle as it enters the tube is :View SolutionA particle of mass 0.1kg is launched at an angle of 53∘ with the horizontal . The particle enters a fixed rough hollow tube whose length is slightly less than 12.5m and which is inclined at an angle of 37∘ with the horizontal as shown in figure. It is known that the velocity of ball when it enters the tube is parallel to the axis of the tube. The coefficient of friction betweent the particle and tube inside the tube is μ=38[ Take g=10m/g2]

The kinetic energy of the particle when it comes out of the tube is approximately equal to :View Solution
Knowledge Check
- Question 1 - Select One
A particle is thrown with a speed is at an angle θ with the horizontal. When the particle makes an angle ϕ with the horizontal, its speed changes to v, then
Av=v0cosθBv=v0cosθ⋅cosϕCv=v0cosθ⋅secϕDv=v0secθ⋅cosϕ
A particle of mass m is projected with velocity making an angle of 45∘ with the horizontal When the particle lands on the level ground the magnitude of the change in its momentum will be .
View SolutionWater rises in a capillary tube to a height 4 cm. If the tube is inclined at an angle of 45∘ with the vertical , find the position of the water in the tube.
View SolutionThe pollen tube enters the ovule through
View SolutionThe range of a projectile, when launched at an angle of 15∘ with the horizontal is 1.5 km. what is the range of the projectile, when launched at an angle of 45∘ to the horizontal with the same speed ?
View SolutionAn incompressible liquid flows through a horizontal tube as shown in the figure. Then the velocity 'v' of the fluid is:
 View Solution
View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is
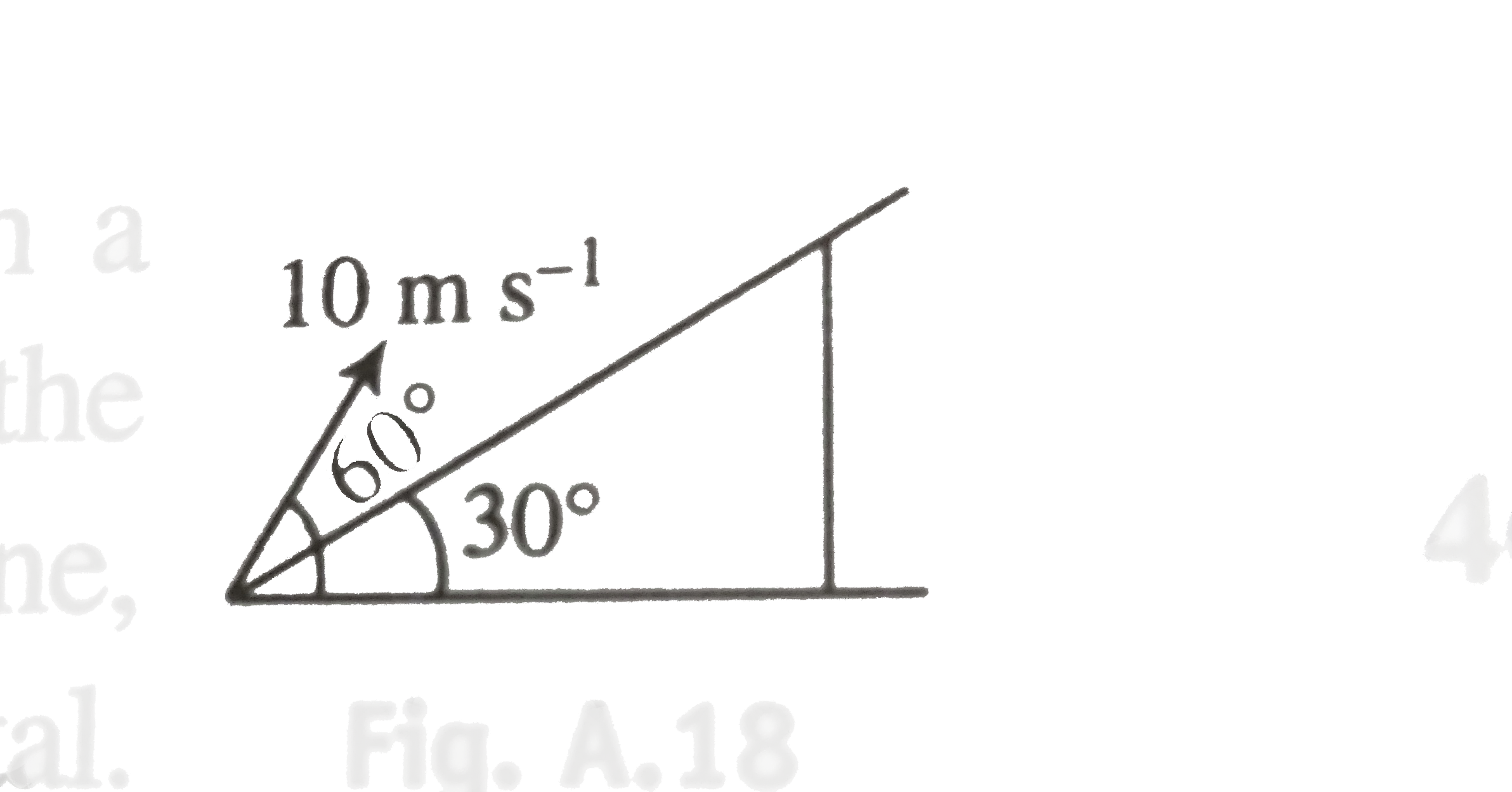 View Solution
View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is
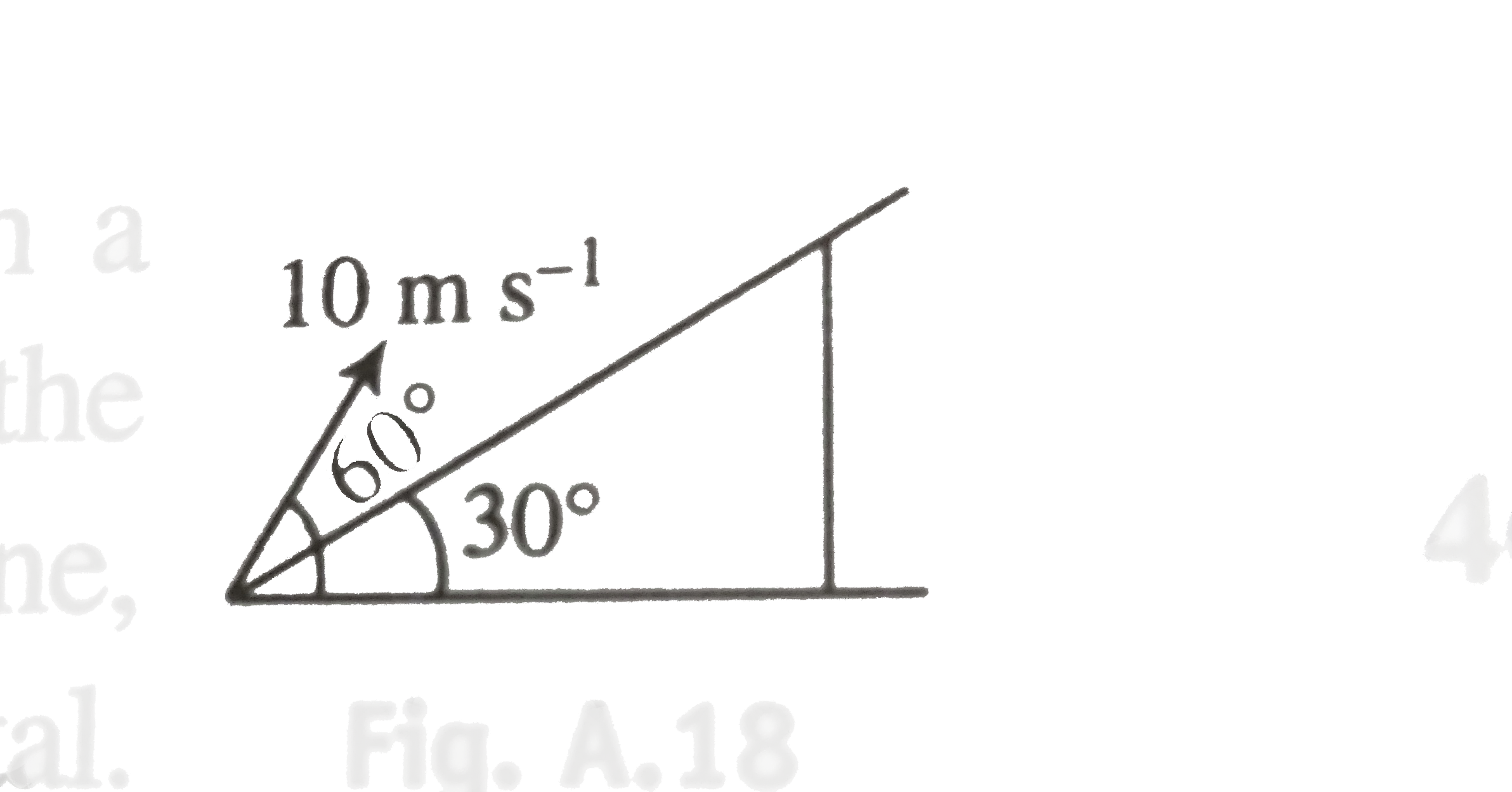 View Solution
View Solution
