A circle, with centre O, circumscribs a pentagon ABCDE. IF AB−BC=CDand∠BCD=126∘, find:
∠AED
The correct Answer is:81∘
To solve the problem step by step, we will follow the reasoning outlined in the video transcript:
Step 1: Understand the Given Information
We have a pentagon ABCDE inscribed in a circle with center O. We know:
- AB−BC=CD
- ∠BCD=126∘
Step 2: Establish Relationships in Triangles
In triangles BOC and COD:
- OB=OD (both are radii of the circle)
- OC=OC (common side)
- BC=CD (from the given information)
Step 3: Apply SSS Criteria for Similarity
Since we have two pairs of equal sides and a common side, triangles BOC and COD are similar by the SSS (Side-Side-Side) criterion.
Step 4: Find Angles OCB and OCD
From the similarity of triangles, we have:
∠OCB=∠OCD=12∠BCD
Substituting the value of ∠BCD:
∠OCB=∠OCD=12×126∘=63∘
Step 5: Find Angle OBC
In triangle BOC, since OB=OC (radii of the circle), we have:
∠OCB=∠OBC
Thus,
∠OBC=63∘
Step 6: Use Angle Sum Property in Triangle BOC
Using the angle sum property of triangle BOC:
∠OBC+∠OCB+∠BOC=180∘
Substituting the known angles:
63∘+63∘+∠BOC=180∘
This simplifies to:
∠BOC=180∘−126∘=54∘
Step 7: Find Angle AOB and COD
Since AB=BC=CD, we can conclude:
∠AOB=∠BOC=∠COD=54∘
Step 8: Find Angle AED
Using the property that the angle subtended by an arc at any point on the circle is half the angle subtended by the same arc at the center:
∠AED=12×(∠AOB+∠BOC+∠COD)
Substituting the values:
∠AED=12×(54∘+54∘+54∘)=12×162∘=81∘
Final Answer
Thus, the measure of ∠AED is:
∠AED=81∘
We have a pentagon ABCDE inscribed in a circle with center O. We know:
- AB−BC=CD
- ∠BCD=126∘
In triangles BOC and COD:
- OB=OD (both are radii of the circle)
- OC=OC (common side)
- BC=CD (from the given information)
Since we have two pairs of equal sides and a common side, triangles BOC and COD are similar by the SSS (Side-Side-Side) criterion.
From the similarity of triangles, we have:
∠OCB=∠OCD=12∠BCD
Substituting the value of ∠BCD:
∠OCB=∠OCD=12×126∘=63∘
In triangle BOC, since OB=OC (radii of the circle), we have:
∠OCB=∠OBC
Thus,
∠OBC=63∘
Using the angle sum property of triangle BOC:
∠OBC+∠OCB+∠BOC=180∘
Substituting the known angles:
63∘+63∘+∠BOC=180∘
This simplifies to:
∠BOC=180∘−126∘=54∘
Since AB=BC=CD, we can conclude:
∠AOB=∠BOC=∠COD=54∘
Using the property that the angle subtended by an arc at any point on the circle is half the angle subtended by the same arc at the center:
∠AED=12×(∠AOB+∠BOC+∠COD)
Substituting the values:
∠AED=12×(54∘+54∘+54∘)=12×162∘=81∘
Thus, the measure of ∠AED is:
∠AED=81∘
Topper's Solved these Questions
Similar Questions
A circle, with centre O, circumscribs a pentagon ABCDE. IF AB−BC=CDand∠BCD=126∘, find:
∠AOC
View SolutionA circle, with centre O, circumscribs a pentagon ABCDE. IF AB−BC=CDand∠BCD=126∘, find:
∠AEB
View SolutionIn cyclic quadrilateral ABCD , AD = BC, ∠BAC=30∘and∠CBD=70∘ , find : angle ADC .
View SolutionABCDE is a cyclic pentagon with centre of its circumcircle alt point O such that AB=BC=CD and angle ABC=120∘
Calculate
(i) ∠BEC (ii) ∠BED
View SolutionIn the given 'O' is the centre of the circle, Arc AB=ArcBC=Cd.If∠OAB=48∘, find:
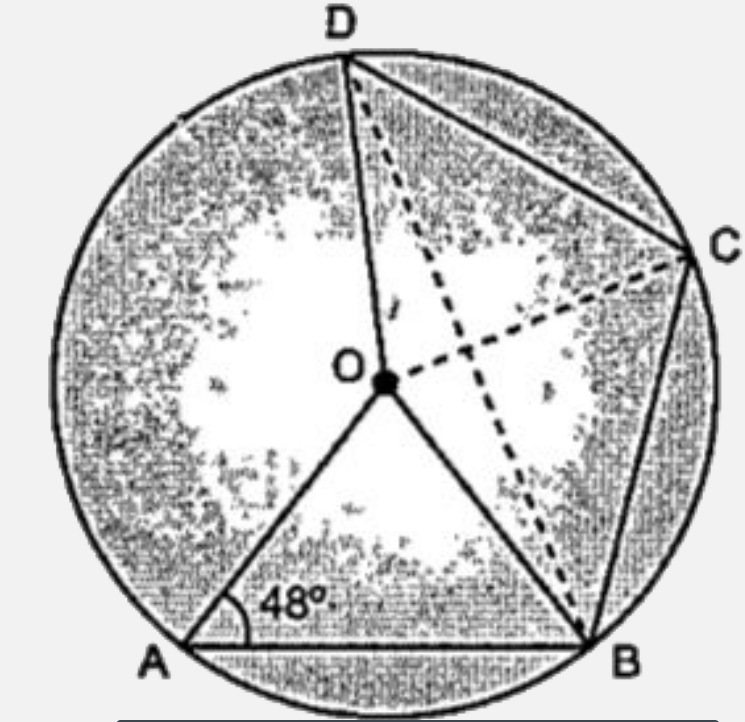
∠OBD
View SolutionIn cyclic quadrilateral ABCD , AD = BC ,∠BAC=30∘and∠CBD=70∘ , find :
∠BCD
View SolutionIn cyclic quadrilateral ABCD , AD = BC ,∠BAC=30∘and∠CBD=70∘ , find :
∠ABC
View SolutionIn cyclic quadrilateral ABCD , AD = BC ,∠BAC=30∘and∠CBD=70∘ , find :
∠BCA
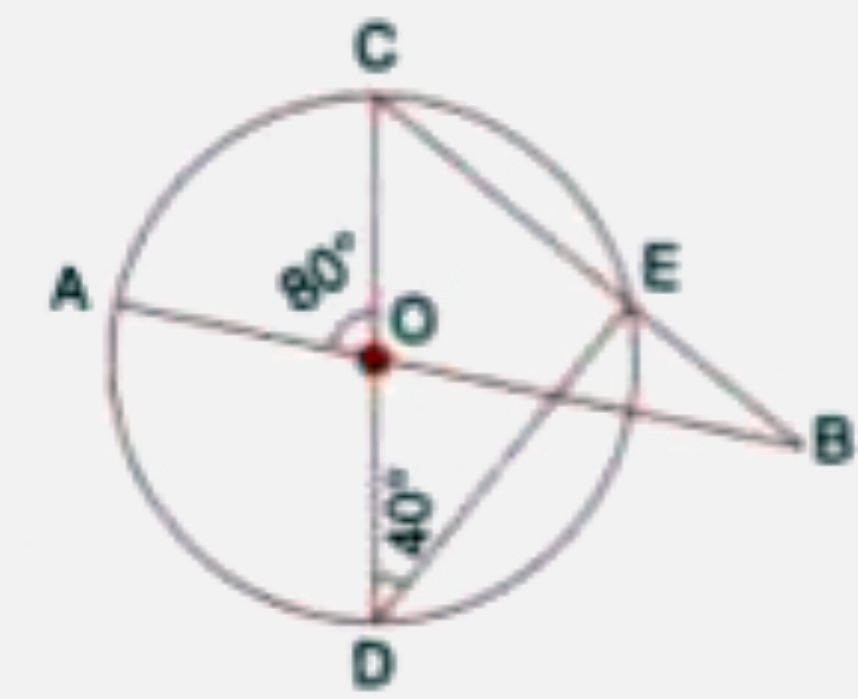
View SolutionIn the figure given alongside ,AB and CD are straight lines thorugh the centre O of a circle. If ∠AOC=80∘and∠CDE=40∘ , find ∠DCE
View SolutionIn a pentagon ABCDE, AB is parallel to DC and ∠A:∠E:∠D=3:4:5. Find angle E.
View Solution
