In the given 'O' is the centre of the circle, Arc find:
The correct Answer is:
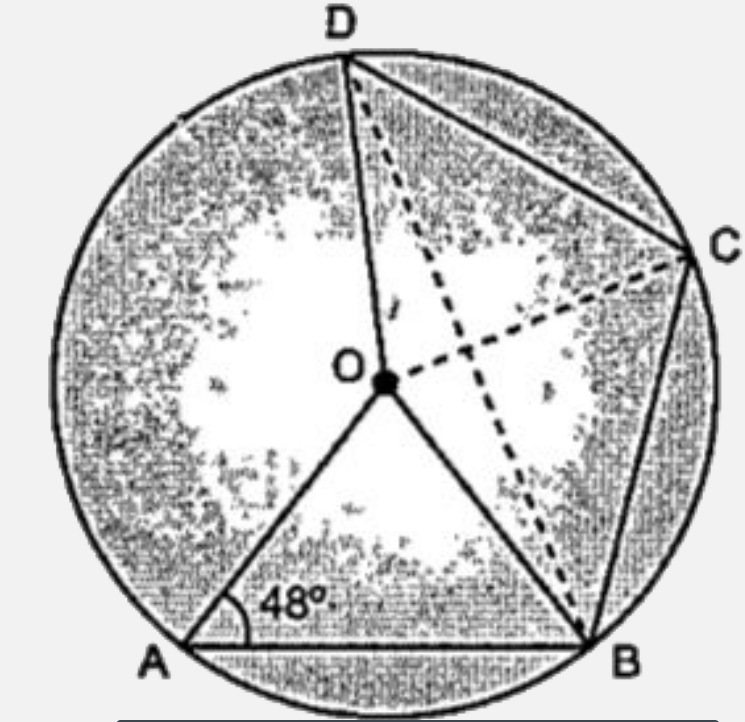
Step by step video & image solution for In the given 'O' is the centre of the circle, Arc AB = Arc BC = Cd. If angle OAB = 48 ^(@), find: angle OBD by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
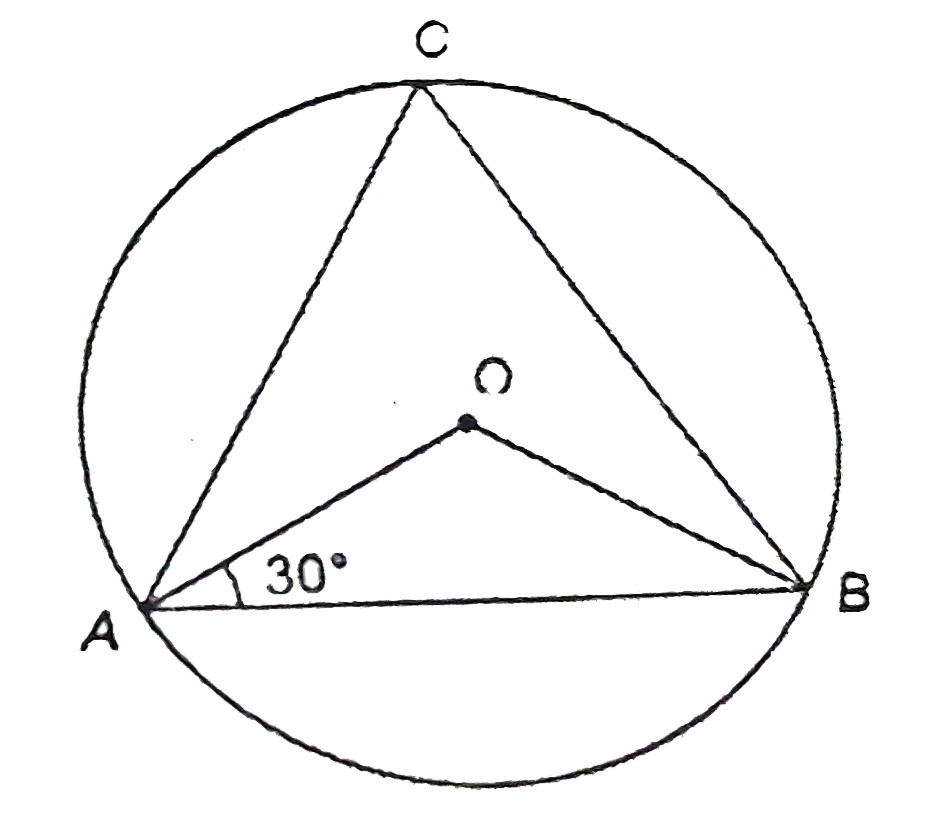
In the adjoining , O is the centre of the circle. ACB is a segment. If ∠OAB=30∘, then find the value of ∠ACB.
View SolutionIn the given figure , AD is a diameter O is the centre of the circle AD is parallel to BC and ∠CBD=32∘
(i) ∠OBD
(ii )∠AOB
(iii) ∠BED
View SolutionIn the given arc AB= twice are BC and ∠AOB=80∘ find:
∠BOC
View SolutionIn the given arc AB= twice are BC and ∠AOB=80∘ find:
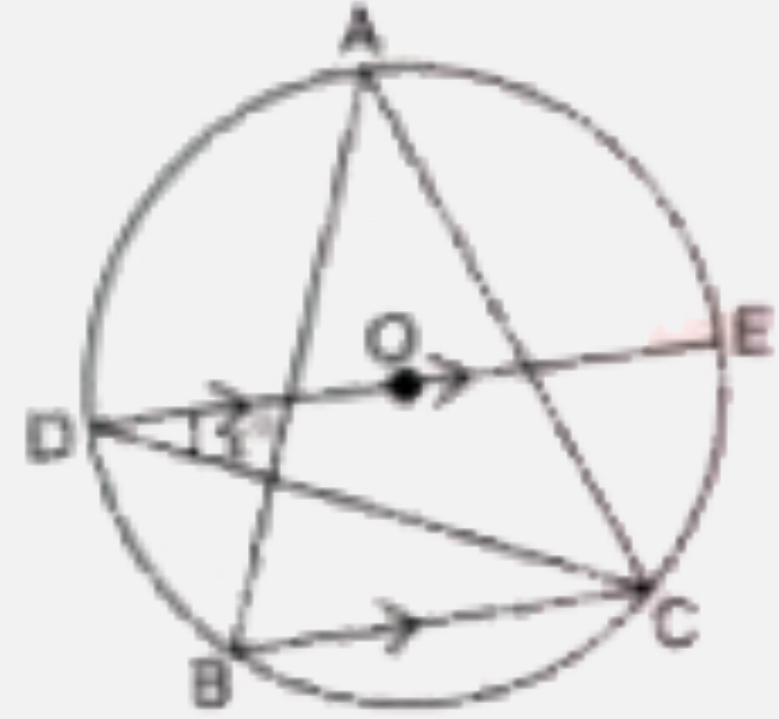
∠OAC
View SolutionIn the given figure BC//DE and O is the centre of the circle . If ∠CDE=x∘ , find in terms of x∘ the value of ∠BAC.
View SolutionIn the given the length of arcs AB and BC are in the ratio 3:2.
If ∠AOB=96∘ find
∠ABC
View SolutionIn the given the length of arcs AB and BC are in the ratio 3:2.
If ∠AOB=96∘ find
∠BOC
View SolutionIn the figure given , O is the centre of the circle . ∠DAE=70∘ , Find the giving suitable reasons , the measure of
(i) ∠BCD
(ii) ∠BOD
(iii) ∠OBD
View SolutionIn the given figure , the lengths of arc AB and are BC arc in the ratio 3: 2 if ∠AOB=96∘, find
(i)∠CAB(ii)∠ADB
View SolutionIn the given diagram 'O is the centre of the circle and AB is parallel to CD. AB = 24 cm and distance between he chord AB and CD is 17 cm. It the radius of the circle is 13 cm, find the length of the chord CD.
View Solution