Show that two equal masses undergo oblique elastic collision will move at right angles after collision , if the second body initialyy at rest . Solution in Telugu

Video Solution

Text Solution

Verified by Experts

Oblique elastic collision : If the centres of mass of the colliding bodies are not initially moving along the line of impact, then the impact is called oblique collision
Two equal masses undergo oblique elastic will move at right angles after collosion,if the second body initially at rest :

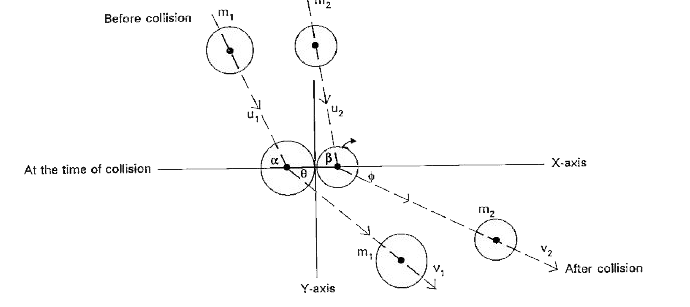
Consider two smooth and perfectly elastic spheres of masses $m_{1} and m_{2} . Let u_{1} and u_{2}$ be their initial velocities before collision . Let $v_{1} and v_{2}$ be their final velocities after collision . $(α, β) and (θ, ϕ)$ are the angles, the directions of motion make with the line of impact before collision and after collision
Since the spheres are smooth, there is no (impulse) change of velocities perpendicular to the time of impact. Hence the resolved part of velocity of the two spheres int he direction perpendicular to the line of impact remain unchanged
$∴ v_{1} sin θ = u_{1} sin α . . . . (1)$
and $v_{2} sin ϕ = u_{2} β . . . (2)$
According to the principle of conservation of momentum, the sum of the moment of the two spheres along the line of impact before collision and after collision are equal .
$∴ m_{1} u_{1} cos α + m_{2} u_{2} cos β = m_{1} v_{1} cos θ + m_{2} v_{2} cos ϕ . . . (3)$
$\to m_{1} (u_{1} cos α - v_{1} cos θ) = m_{2} (v_{2} cos ϕ - u_{2} cos β) . . . . (4)$
According to the principle of conservation of kinetic energy, the sum of the K.E along the lien of impact before and after are equal
$∴ \frac{1}{2} m_{1} {(u_{1} cos α)}_{1}^{2} + \frac{1}{2} m_{2} {(u_{2} cos β)}_{2}^{2} = \frac{1}{2} m_{1} {(v_{1} cos θ)}_{1}^{2} + \frac{1}{2} m_{2} {(v_{2} cos ϕ)}_{2}^{2}$
$m_{1} [{(u_{1} cos α)}_{1}^{2} - {(v_{1} cos θ)}_{1}^{2}] = m_{2} [{(v_{2} cos ϕ)}_{2}^{2} - {(u_{2} cos β)}_{2}^{2}] . . . (5)$
$\frac{(5)}{(4)} \Rightarrow u_{1} cos α + v_{1} cos θ = (v_{2} cos ϕ + v_{2} cos β)$
$v_{1} cos θ = v_{2} cos ϕ + u_{2} cos β - u_{1} cos α . . . . (6)$
and $v_{2} cos ϕ = v_{1} cos θ + u_{1} cos α - u_{2} cos β . . . . (7)$
sub. equation (6) in equation (3) , we get
$v_{1} cos θ = (\frac{m_{2} - m_{1}}{m_{1} + m_{2}}) u_{1} cos α + 2 (\frac{m_{2} u_{2}}{m_{1} + m_{2}}) cos β . . . . (8)$
and $v_{2} cos ϕ = (\frac{m_{2} - m_{1}}{m_{1} + m_{2}}) u_{2} cos β + (\frac{2 m_{1} u_{1}}{m_{1} = m_{2}}) cos α . . . (9)$
If $u_{2} = 0 and m_{1} = m_{2}$ then equation (2) we get $ϕ = 0$ and from equation $(8), θ = 90^{\circ}$ . This means that if a sphere of mass .m. collides obliquely on another perfectly elastic sphere of the same mass at rest the directions of motions of the spheres after impact will be at right angles

Updated on:21/07/2023

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile