When two spheres of equal masses undergo glancing elastic collision with one of them at rest after collision they will move
opposite to one another
in the same direction
together
at right angle to each other
The correct Answer is:D
To solve the problem of two spheres of equal masses undergoing a glancing elastic collision, we can follow these steps:
Step 1: Understand the scenario
We have two spheres, both with equal mass m. One sphere is moving with an initial velocity u1 and the other sphere is at rest, so its initial velocity u2=0.
Step 2: Apply the conservation of momentum
In an elastic collision, the total momentum before the collision is equal to the total momentum after the collision. Mathematically, this can be expressed as:
mu1+mu2=mv1+mv2
Since u2=0, this simplifies to:
mu1=mv1+mv2
Dividing through by m gives:
u1=v1+v2
Step 3: Apply the conservation of kinetic energy
In an elastic collision, the total kinetic energy before the collision is equal to the total kinetic energy after the collision. This can be expressed as:
12mu21+12mu22=12mv21+12mv22
Again, since u2=0, this simplifies to:
12mu21=12mv21+12mv22
Dividing through by 12m gives:
u21=v21+v22
Step 4: Analyze the angles
In a glancing collision, the two spheres will move off at right angles to each other after the collision. Thus, we can denote the angle between their velocities as 90∘. This means:
v21+v22=(u1)2
This confirms that the velocities v1 and v2 are perpendicular to each other.
Conclusion
From the above analysis, we conclude that after the collision, the two spheres will move at right angles to each other, confirming the statement in the question.
---
We have two spheres, both with equal mass m. One sphere is moving with an initial velocity u1 and the other sphere is at rest, so its initial velocity u2=0.
In an elastic collision, the total momentum before the collision is equal to the total momentum after the collision. Mathematically, this can be expressed as:
mu1+mu2=mv1+mv2
Since u2=0, this simplifies to:
mu1=mv1+mv2
Dividing through by m gives:
u1=v1+v2
In an elastic collision, the total kinetic energy before the collision is equal to the total kinetic energy after the collision. This can be expressed as:
12mu21+12mu22=12mv21+12mv22
Again, since u2=0, this simplifies to:
12mu21=12mv21+12mv22
Dividing through by 12m gives:
u21=v21+v22
In a glancing collision, the two spheres will move off at right angles to each other after the collision. Thus, we can denote the angle between their velocities as 90∘. This means:
v21+v22=(u1)2
This confirms that the velocities v1 and v2 are perpendicular to each other.
From the above analysis, we conclude that after the collision, the two spheres will move at right angles to each other, confirming the statement in the question.
Topper's Solved these Questions
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - NCERT
18 Videos
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - ASSERTION & REASON
15 Videos
- WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A body (solid sphere) of mass m makes an elastic collision with another idential body at rest. Just after collision the angle between the velocity vector of one body with the initial line of motion is 15∘ then the angle between velocity vector of the other body with the initial line of motion is
View SolutionIn an elastic collision between two particles
View SolutionIn a head on elastic collision of two bodies of equal masses
View SolutionTwo identical balls moving in opposite directions with speed 20 m/s and 25 m/s undergo head on perfectly inelastic collision. The speed of combined mass after collision is
View SolutionTwo identical billiard balls undergo an oblique elastic collision. Initially, one of the balls is stationary. If the initially stationary ball after collision moves in a direction which makes an angle of 37∘ with direction of initial motion of the moving ball, then the angle through which initially moving ball will be deflected is
View SolutionA disk A of radious r moving on perfectly smooth surface at a speed v undergoes an elastic collision with an identical stationary disk B. Find the velocity of the disk B after collision if the impact parameter is r/2 as shown in the figure :-
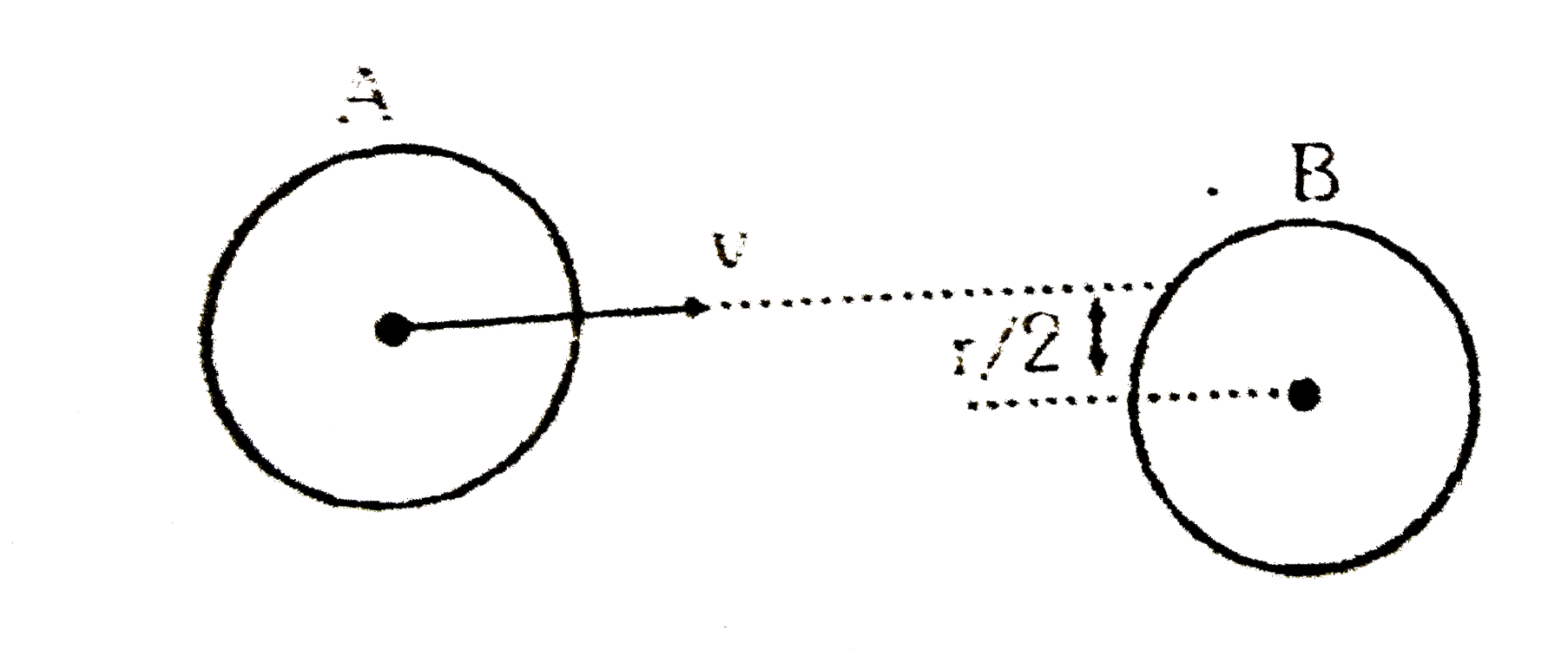
View SolutionA moving sphere of mass m suffer a perfect elastic collision (not head on) with equally massive stationary sphere. After collision both fly off at angle θ, value of which is :
View SolutionA smooth sphere of mass M moving with velocity u directly collides elastically with another sphere of mass m at rest. After collision their final velocities are V and v respectively. The value of v is
View SolutionA smooth sphere of mass M moving with velocity u directly collides elastically with another sphere of mass m at rest. After collision their final velocities are V and v respectively. The value of v is
View SolutionMaximum energy transfer for an elastic collision will occur if one body is at rest when
View Solution
