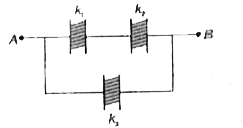
If CAB (equivalent ) = C2 and capacitance of all the capacitors are C in vacuum without dielectric . Find the relation between k1.k2.k3
∵CAB=(Ck1×Ck2Ck1+Ck2)=Ck3
⇒C2=C2C(k1k2k1+k2)+Ck3
⇒12=k1k2k1+k2+k3
⇒12=k1k2+k1k3+k2k3k1+k2
⇒k1+k22=(k1k2+k1k3+k2k3)
Similar Questions
Find the equivalent capacitance between A and B. All the capacitors have capacitance C.

View SolutionFind the equivalent capacitance between A and B. All the capacitors have capacitance C.

View SolutionThe equivalent capacitance of three capacitors of capacitance C1:C2 and C3 are connected in parallel is 12 units and product C1.C2.C3=48. When the capacitors C1 and C2 are connected in parallel, the equivalent capacitance is 6 units. then the capacitance are
View SolutionIn the figure a capacitor is filled with dielectrics K1,K2 and K3. The resultant capacitance is
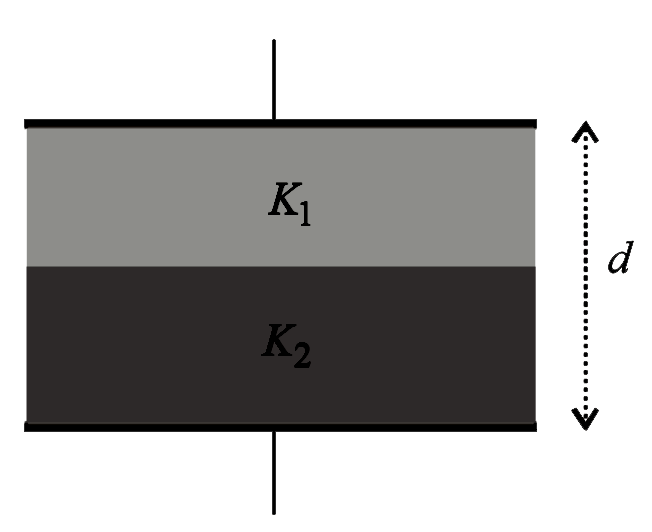
View SolutionA parallel plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials hving dielectric constants K1,K2,K3 and K4 as shown in the figure below. If a single dielectric material is to be used to have the same capacitance c in this capacitor, then its dielectric constant K is given by

View SolutionA parallel plate capacitor has a dielectric slab of dielectric constant K between its plates that covers 1/3 of the area of its plates, as shown in the figure. The total capacitance of the capacitor is C while that of the portion with dielectric in between is C1. When the capacitor is charged, the plate area covered by the dielectric gets charge Q1 and the rest of the area gets charge Q2. The electric field in the dielectric is E1 and that in the other portion is E2. Choose the correct option/options, ignoring edge effects.

View SolutionObtain an expression for equivalent capacitance when three capacitors C1,C2andC3 are connected in series.
View SolutionDeduce an expression for equivalent capacitance C when three capacitors C1,C2andC3 are connected in parallel.
View SolutionFind the capacitance between A and B if three dielectric slabs of dielectric constants K1areaA _(2)andthick≠ssd_(2))are∈sertedbetweentheplatesofaparal≤llate∩aci→rofplateareaA.(Giventˆthedistancebetweenthetwoplatesisd_(1)=d_(2)+d_(2).)
 .
.
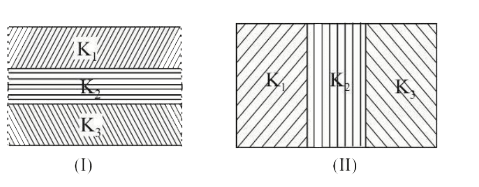
View SolutionTwo identical parallel plate capacitors, of capacitance C each, have plates of area A, separated by a distance d. The space between the plates of the two capacitors, is filled with three dielectrics, of equal thickness and dielectric constants K1,K2andK3. The first capacitor is filled as shown in fig. I, and the second one is filled as shown in fig. II. If these two modified capacitors are charged by the same potential V, the ratio of the energy stored in the two, would be (E1 refers to capacitor (I) and E2 to capacitor (II)):
View Solution
