Two parallel plates capacitors A and B having capacitance of $1 μ F and 5 μ F$ are charged separately to the same potential of 100 V. Now, the positive plate of A is connected to the negative plate of B and the negative plate of A to the positive plate of B. Find the final charges on each capacitors.

Video Solution

Text Solution

Verified by Experts

As for a capacitor q =CV so initially the charge on each capacitor .
$q_{1} = C_{1} V_{1} = (1 \times 10^{- 6}) \times 100 = 100 μ C$
and $q_{2} = C_{2} V_{2} = (5 \times 10^{- 6}) \times 100 = 500 μ C$
Now when two capacitors are joined to each other such that positive plate of one is connected with the negative of the other by conservation of charge $q = q_{1} + q_{2} = | q_{1} | - | q_{2} | = (500 - 100) μ C = 400 μ C .$ So common potential
$V = \frac{(q_{1} + q_{2})}{(C_{1} + C_{2})} = \frac{400 \times 10^{- 6}}{(1 \div 5) \times 10^{- 6}} = \frac{200}{3} V$
And hence after sharing charge on each capacitor
$q_{1} = C_{1} V = (1 \times 10^{- 6}) \times \frac{200}{3} = \frac{200}{3} μ C$
$q_{2} = C_{2} V = (5 \times 10^{- 6}) \times \frac{200}{3} = \frac{1000}{3} μ C$

Updated on:21/07/2023

The potential difference between points $A$ and $B$ is

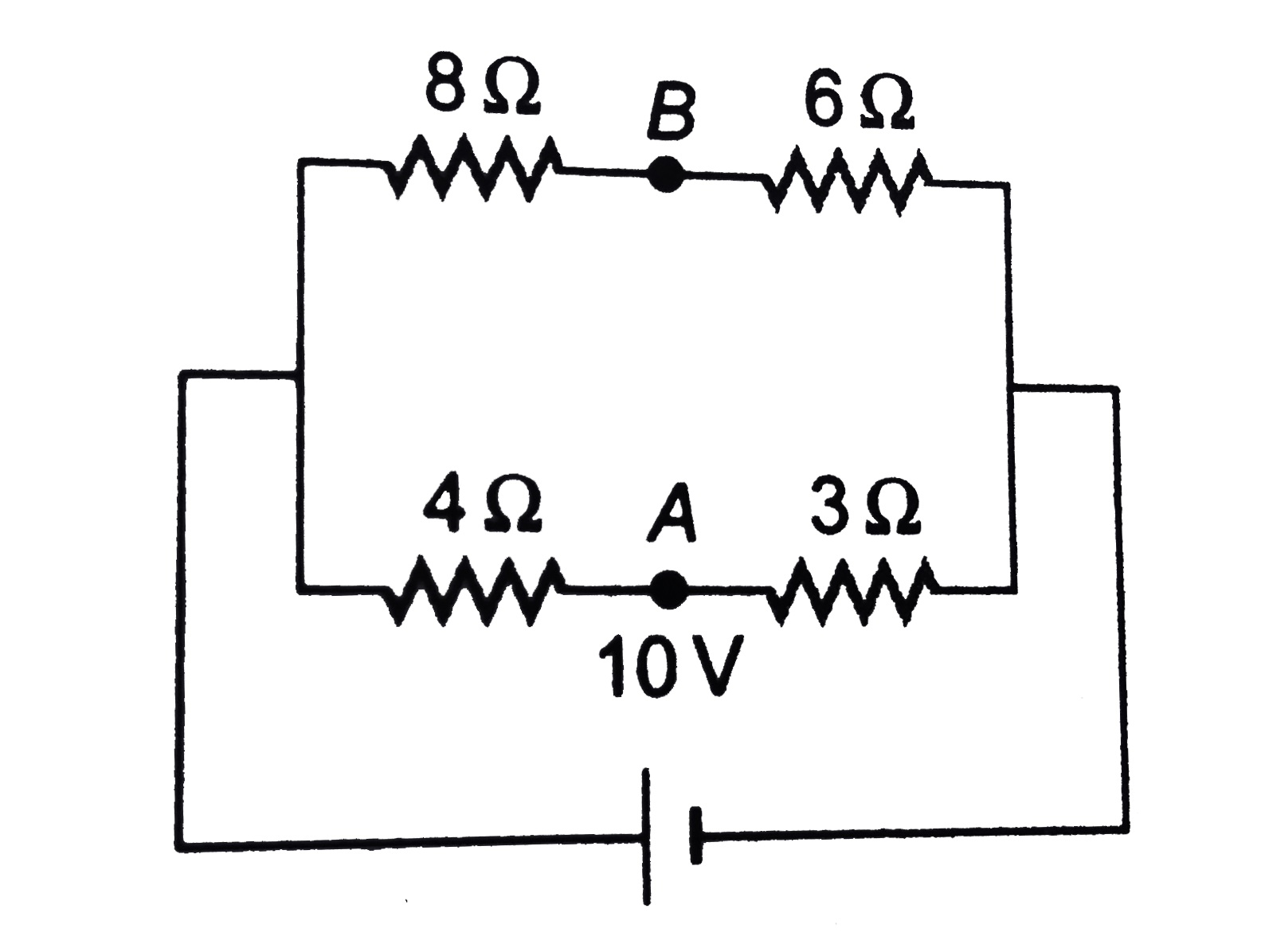A2
B5
C11
D18
Two idential capacitors are joined in parallel, charged to a potential $V$ and then separated and then connected in series i.e. the positive plate of one is connected to negative of the other
AThe charges on the free plated connected together are destoyed.
BThe energy stored in the system increases.
CThe potential difference between the free plates is 2V.
DThe potential difference remains constant.